Linked Comprehension Type Question from G.R. BATHLA & SONS CHEMISTRY Chapter 3 ATOMIC STRUCTURE for Class 11

Class 11	CHEMISTRY
Chapter	ATOMIC STRUCTURE
G.R. BATHLA & SONS CHEMISTRY	Linked Comprehension Type Question
Medium	English
Academic Year	2023-2024

Question 1
The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
$\frac{1}{λ} = R_{H} [\frac{1}{2^{2}} - \frac{1}{n^{2}}] n = 3, 4, 5$ . . .
$R_{H} = 109678 c m^{- 1}$ is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
Q. Calculat ethe longest wavelength in Ã…(1Ã…= $10^{- 10} m$ ) in the balmer series of singly ionized helium $H e^{+}$ . Select the correct answer. Ignore the nuclear motion in your calculation. View Solution
Question 2
The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
$\frac{1}{λ} = R_{H} [\frac{1}{2^{2}} - \frac{1}{n^{2}}] n = 3, 4, 5$ . . .
$R_{H} = 109678 c m^{- 1}$ is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.Howmany lines in the spectrum will be observed when electrons return from 7th shell to 2nd shell?View Solution
Question 3
The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
$\frac{1}{λ} = R_{H} [\frac{1}{2^{2}} - \frac{1}{n^{2}}] n = 3, 4, 5$ . . .
$R_{H} = 109678 c m^{- 1}$ is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
The wavelength of first line of Balmer spectrum of hydrogen will be:View Solution
Question 4
The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
$\frac{1}{λ} = R_{H} [\frac{1}{2^{2}} - \frac{1}{n^{2}}] n = 3, 4, 5$ . . .
$R_{H} = 109678 c m^{- 1}$ is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
Q.In which region of electromagnetic spectrum does the Balmer series lie?View Solution
Question 5
The observed wavelegnth in the line spectrum of hydrogen atom were first expressed in terms of a series by Johann Jakob Balmer, a Swiss teacher.
Balmer's emipirical formula is
$\frac{1}{λ} = R_{H} [\frac{1}{2^{2}} - \frac{1}{n^{2}}] n = 3, 4, 5$ . . .
$R_{H} = 109678 c m^{- 1}$ is the Rydberg constant.
Niels Bohr derived this expression theoretically in 1913. The formula is generalised to any one electron atom/ion.
Which of the following is not correctly matched?View Solution
Question 6
A formula analogous to Rydberg formula applies to the series of spectral ines which arise from transition from higher energy level to the lower energy level of hydrogen atom.
A muonic hydrogen atom is like a hydrogen atom in which the electron is replaced by a heavier particle,t he 'muon'. the mass of the muon is about 207 times the mass of an electron, while the charge remains same as that of the electron. Rydberg formula for hydrogen atom is:
$\frac{1}{λ} = R_{H} [\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}}] (R_{H} = 109678 c m^{- 1})$
Q. Radius of first Bohr orbit of muonic hydrogen atom is:View Solution
Question 7
A formula analogous to Rydberg formula applies to the series of spectral ines which arise from transition from higher energy level to the lower energy level of hydrogen atom.
A muonic hydrogen atom is like a hydrogen atom in which the electron is replaced by a heavier particle,t he 'muon'. the mass of the muon is about 207 times the mass of an electron, while the charge remains same as that of the electron. Rydberg formula for hydrogen atom is:
$\frac{1}{λ} = R_{H} [\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}}] (R_{H} = 109678 c m^{- 1})$
Q. Energy of first Bohr orbit of muonic hydrogen atom is:View Solution
Question 8
A formula analogous to Rydberg formula applies to the series of spectral ines which arise from transition from higher energy level to the lower energy level of hydrogen atom.
A muonic hydrogen atom is like a hydrogen atom in which the electron is replaced by a heavier particle,t he 'muon'. the mass of the muon is about 207 times the mass of an electron, while the charge remains same as that of the electron. Rydberg formula for hydrogen atom is:
$\frac{1}{λ} = R_{H} [\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}}] (R_{H} = 109678 c m^{- 1})$
Q. View Solution
Question 9
A formula analogous to Rydberg formula applies to the series of spectral ines which arise from transition from higher energy level to the lower energy level of hydrogen atom.
A muonic hydrogen atom is like a hydrogen atom in which the electron is replaced by a heavier particle,t he 'muon'. the mass of the muon is about 207 times the mass of an electron, while the charge remains same as that of the electron. Rydberg formula for hydrogen atom is:
$\frac{1}{λ} = R_{H} [\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}}] (R_{H} = 109678 c m^{- 1})$
Q. Angular momentum of 'muon' in muonic hydrogen atom may be given as:View Solution
Question 10
A formula analogous to Rydberg formula applies to the series of spectral ines which arise from transition from higher energy level to the lower energy level of hydrogen atom.
A muonic hydrogen atom is like a hydrogen atom in which the electron is replaced by a heavier particle,t he 'muon'. the mass of the muon is about 207 times the mass of an electron, while the charge remains same as that of the electron. Rydberg formula for hydrogen atom is:
$\frac{1}{λ} = R_{H} [\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}}] (R_{H} = 109678 c m^{- 1})$
Q. Distance between first and third Bohr orbits of muonic hydrogen atom will be:View Solution
Question 11
The wave function $Φ_{n, l, m_{1}}$ is a methematical function whose value depends upon shperical upon spherical polar coordinates $(r, θ, ϕ)$ of the electron and characterized by the quantum numbers, n,l and $m_{1}$ . Here r is distance from nucleus, $θ$ is colatitude and $ϕ$ is azimuth. in the mathematical functions given in the table, Z is atomic number, $a_{0}$ is Bohr radius.
.
Q. For the given orbital in column 1, the only correct combination forany hydrogen-like species is:View Solution
Question 12
The wave function $Φ_{n, l, m_{1}}$ is a methematical function whose value depends upon shperical upon spherical polar coordinates $(r, θ, ϕ)$ of the electron and characterized by the quantum numbers, n,l and $m_{1}$ . Here r is distance from nucleus, $θ$ is colatitude and $ϕ$ is azimuth. in the mathematical functions given in the table, Z is atomic number, $a_{0}$ is Bohr radius.
.
Q. For $H e^{+}$ ion, the only INCORRECT combination is:View Solution
Question 13
The wave function $Φ_{n, l, m_{1}}$ is a methematical function whose value depends upon shperical upon spherical polar coordinates $(r, θ, ϕ)$ of the electron and characterized by the quantum numbers, n,l and $m_{1}$ . Here r is distance from nucleus, $θ$ is colatitude and $ϕ$ is azimuth. in the mathematical functions given in the table, Z is atomic number, $a_{0}$ is Bohr radius.
.
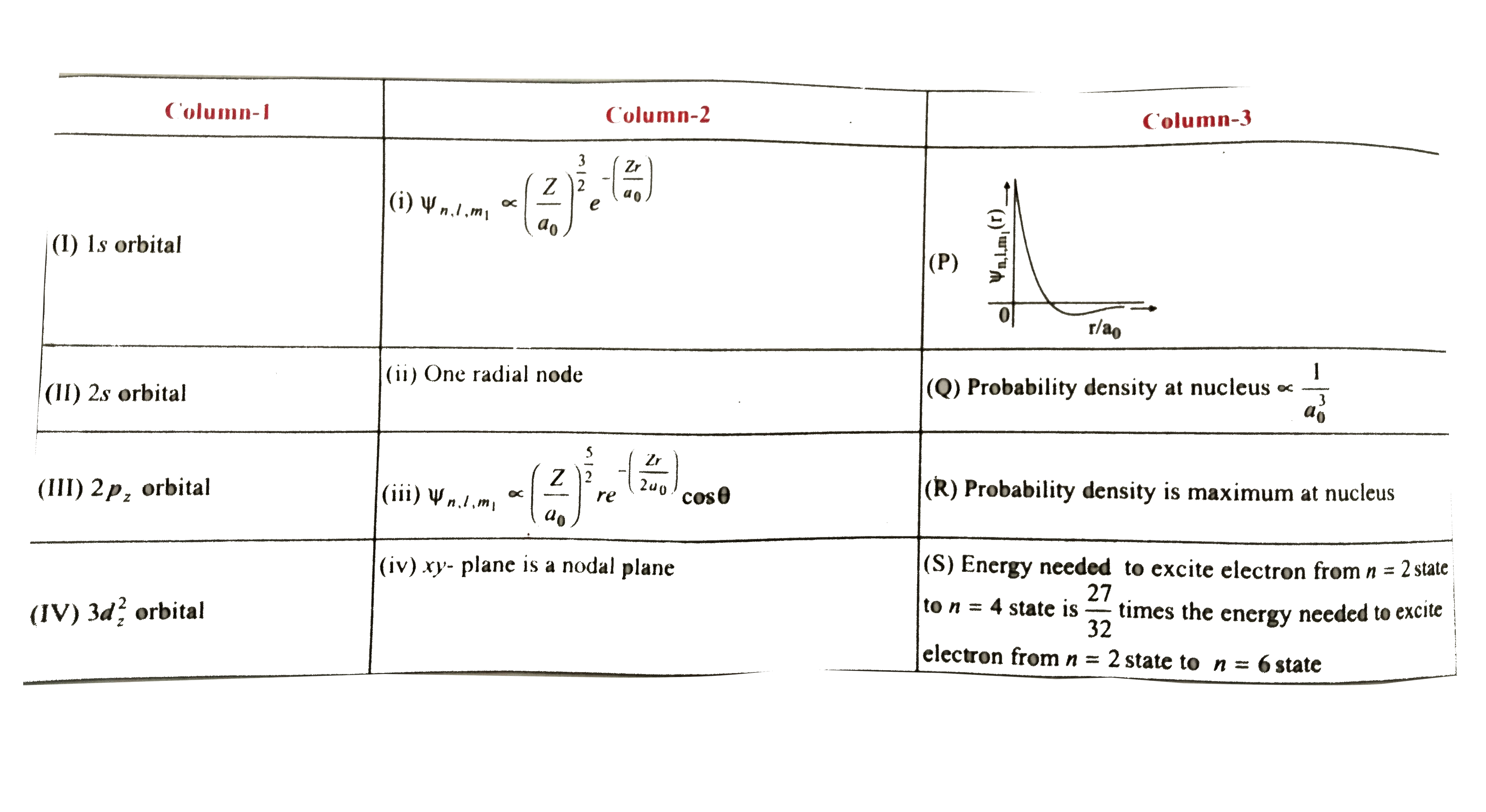Q. For hydrogen atom the only CORRECT combination is : View Solution
Question 14
The substances which contain species with unpaired electrons in their orbitals behave as paramagnetic sustances. Such substances are weakly attracted by the magnetic field. The paramagnetism is expressed in terms of magnetic moment. The magnetic moment is related to the number of unpaired electrons according tot he following relation:
Magnetic moment $μ = \sqrt{n (n + 2)} B M$
where n=number of unpaired electrons.
BM stands for Bohr magneton, a unit of magnetic moment.
$1 B M = \frac{e h}{4 π m c} = 9.27 \times 10^{- 24} A m^{2}$ or $J T^{- 1}$
Q. Which of the following ions has the highest magnetic moment?View Solution
Question 15
The substances which contain species with unpaired electrons in their orbitals behave as paramagnetic sustances. Such substances are weakly attracted by the magnetic field. The paramagnetism is expressed in terms of magnetic moment. The magnetic moment is related to the number of unpaired electrons according tot he following relation:
Magnetic moment $μ = \sqrt{n (n + 2)} B M$
where n=number of unpaired electrons.
BM stands for Bohr magneton, a unit of magnetic moment.
$1 B M = \frac{e h}{4 π m c} = 9.27 \times 10^{- 24} A m^{2}$ or $J T^{- 1}$
Q. Which of the following ions has magnetic moment equal to that of $T i^{3 +}$ ?View Solution
Question 16
The substances which contain species with unpaired electrons in their orbitals behave as paramagnetic sustances. Such substances are weakly attracted by the magnetic field. The paramagnetism is expressed in terms of magnetic moment. The magnetic moment is related to the number of unpaired electrons according tot he following relation:
Magnetic moment $μ = \sqrt{n (n + 2)} B M$
where n=number of unpaired electrons.
BM stands for Bohr magneton, a unit of magnetic moment.
$1 B M = \frac{e h}{4 π m c} = 9.27 \times 10^{- 24} A m^{2}$ or $J T^{- 1}$
Q. An ion of a d-block element has magnetic moment 5.92 BM. Select the ion among the following:View Solution
Question 17
The substances which contain species with unpaired electrons in their orbitals behave as paramagnetic sustances. Such substances are weakly attracted by the magnetic field. The paramagnetism is expressed in terms of magnetic moment. The magnetic moment is related to the number of unpaired electrons according tot he following relation:
Magnetic moment $μ = \sqrt{n (n + 2)} B M$
where n=number of unpaired electrons.
BM stands for Bohr magneton, a unit of magnetic moment.
$1 B M = \frac{e h}{4 π m c} = 9.27 \times 10^{- 24} A m^{2}$ or $J T^{- 1}$
Q. In Which of these options do both constituents of the pair have the same magnetic moment?View Solution
Question 18
The substances which contain species with unpaired electrons in their orbitals behave as paramagnetic sustances. Such substances are weakly attracted by the magnetic field. The paramagnetism is expressed in terms of magnetic moment. The magnetic moment is related to the number of unpaired electrons according tot he following relation:
Magnetic moment $μ = \sqrt{n (n + 2)} B M$
where n=number of unpaired electrons.
BM stands for Bohr magneton, a unit of magnetic moment.
$1 B M = \frac{e h}{4 π m c} = 9.27 \times 10^{- 24} A m^{2}$ or $J T^{- 1}$
Q. Which of the following ions are diamagnetic?View Solution
Question 19
At the suggestion of Earnest Rutherford, hans Geiger and ernest Marsden bombarded a thin gold foil by $α$ -particles from a polonium source. It was expected that $α$ -particles would go right through the foil with hardly any deflection. Although, most of the alpha particles indeed were not deviated by much, a few were scattered through veryi large angles. Some were even scattered in the backward direction. The nly way to explain the results, rutherford found, was to picture an atom as being compoed of a tiny nucleus in which its positive charge and nearly all its mass are concentrated. Scattering of $α$ -particles is proportional to target thickness and is inversely proportional to the fourth power of $sin (\frac{θ}{2})$ , where, $θ$ is scattering angle. Distance of closest approach may be calculated as:
$r_{min} = \frac{Z_{1} Z_{2} e^{2}}{4 π ε_{0} K}$
where, K=kinetic energy of $α$ -particles.
Q. Rutherford's $α$ -particle scattering led to the conclusion that:View Solution
Question 20
At the suggestion of Earnest Rutherford, hans Geiger and ernest Marsden bombarded a thin gold foil by $α$ -particles from a polonium source. It was expected that $α$ -particles would go right through the foil with hardly any deflection. Although, most of the alpha particles indeed were not deviated by much, a few were scattered through veryi large angles. Some were even scattered in the backward direction. The nly way to explain the results, rutherford found, was to picture an atom as being compoed of a tiny nucleus in which its positive charge and nearly all its mass are concentrated. Scattering of $α$ -particles is proportional to target thickness and is inversely proportional to the fourth power of $sin (\frac{θ}{2})$ , where, $θ$ is scattering angle. Distance of closest approach may be calculated as:
$r_{min} = \frac{Z_{1} Z_{2} e^{2}}{4 π ε_{0} K}$
where, K=kinetic energy of $α$ -particles.
Q. From the $α$ -particle scattering experiemnt, rutherfod concluded that:View Solution
Question 21
At the suggestion of Earnest Rutherford, hans Geiger and ernest Marsden bombarded a thin gold foil by $α$ -particles from a polonium source. It was expected that $α$ -particles would go right through the foil with hardly any deflection. Although, most of the alpha particles indeed were not deviated by much, a few were scattered through veryi large angles. Some were even scattered in the backward direction. The nly way to explain the results, rutherford found, was to picture an atom as being compoed of a tiny nucleus in which its positive charge and nearly all its mass are concentrated. Scattering of $α$ -particles is proportional to target thickness and is inversely proportional to the fourth power of $sin (\frac{θ}{2})$ , where, $θ$ is scattering angle. Distance of closest approach may be calculated as:
$r_{min} = \frac{Z_{1} Z_{2} e^{2}}{4 π ε_{0} K}$
where, K=kinetic energy of $α$ -particles.
Q. Rutherford's scattering formula fails for vary small scattering angles because:View Solution
Question 22
At the suggestion of Earnest Rutherford, hans Geiger and ernest Marsden bombarded a thin gold foil by $α$ -particles from a polonium source. It was expected that $α$ -particles would go right through the foil with hardly any deflection. Although, most of the alpha particles indeed were not deviated by much, a few were scattered through veryi large angles. Some were even scattered in the backward direction. The nly way to explain the results, rutherford found, was to picture an atom as being compoed of a tiny nucleus in which its positive charge and nearly all its mass are concentrated. Scattering of $α$ -particles is proportional to target thickness and is inversely proportional to the fourth power of $sin (\frac{θ}{2})$ , where, $θ$ is scattering angle. Distance of closest approach may be calculated as:
$r_{min} = \frac{Z_{1} Z_{2} e^{2}}{4 π ε_{0} K}$
where, K=kinetic energy of $α$ -particles.
Q. Alpha particles that come closer to the nuclei:View Solution
Question 23
At the suggestion of Earnest Rutherford, hans Geiger and ernest Marsden bombarded a thin gold foil by $α$ -particles from a polonium source. It was expected that $α$ -particles would go right through the foil with hardly any deflection. Although, most of the alpha particles indeed were not deviated by much, a few were scattered through veryi large angles. Some were even scattered in the backward direction. The nly way to explain the results, rutherford found, was to picture an atom as being compoed of a tiny nucleus in which its positive charge and nearly all its mass are concentrated. Scattering of $α$ -particles is proportional to target thickness and is inversely proportional to the fourth power of $sin (\frac{θ}{2})$ , where, $θ$ is scattering angle. Distance of closest approach may be calculated as:
$r_{min} = \frac{Z_{1} Z_{2} e^{2}}{4 π ε_{0} K}$
where, K=kinetic energy of $α$ -particles.
Q. Which of the following quantities will be zero for alpha particles at the point of closest approach to the gold atom, in Rutherford's scattering of alpha particles?View Solution
Question 24
The splitting of spectral lines by a magnetic field is called the zeeman effect after the Dutch physicist Pieter Zeeman. The Zeeman effect is a vivid confirmation of of space quantization. Magnetic quantum number 'm' was introduced during the study of zeeman effect. 'm' can have the (2l+1) values (-l,0,+l). Magnetic quantum number represents the orientation of atomic orbitals in three-dimensional space. the normal zeeman effect consists of the splitting of a spectral line of frequency $v_{0}$ into three components i.e.,
$v_{1} = v_{0} - \frac{e}{4 π m} B, v_{2} = v_{0}, V_{3} = v_{0} + \frac{e}{4 π m} B$
Here, B is magnetic field.
Q. Which of the following statements is incorrect with reference to the Zeeman effect?View Solution
Question 25
The splitting of spectral lines by a magnetic field is called the zeeman effect after the Dutch physicist Pieter Zeeman. The Zeeman effect is a vivid confirmation of of space quantization. Magnetic quantum number 'm' was introduced during the study of zeeman effect. 'm' can have the (2l+1) values (-l,0,+l). Magnetic quantum number represents the orientation of atomic orbitals in three-dimensional space. the normal zeeman effect consists of the splitting of a spectral line of frequency $v_{0}$ into three components i.e.,
$v_{1} = v_{0} - \frac{e}{4 π m} B, v_{2} = v_{0}, V_{3} = v_{0} + \frac{e}{4 π m} B$
Here, B is magnetic field.
Q. A d-subshell in an atom in the presence and absence of magnetic field is:View Solution
Question 26
The splitting of spectral lines by a magnetic field is called the zeeman effect after the Dutch physicist Pieter Zeeman. The Zeeman effect is a vivid confirmation of of space quantization. Magnetic quantum number 'm' was introduced during the study of zeeman effect. 'm' can have the (2l+1) values (-l,0,+l). Magnetic quantum number represents the orientation of atomic orbitals in three-dimensional space. the normal zeeman effect consists of the splitting of a spectral line of frequency $v_{0}$ into three components i.e.,
$v_{1} = v_{0} - \frac{e}{4 π m} B, v_{2} = v_{0}, V_{3} = v_{0} + \frac{e}{4 π m} B$
Here, B is magnetic field.
Q. Which among the following is/are correct about the orientation of atomic orbitals in space?View Solution
Question 27
The splitting of spectral lines by a magnetic field is called the zeeman effect after the Dutch physicist Pieter Zeeman. The Zeeman effect is a vivid confirmation of of space quantization. Magnetic quantum number 'm' was introduced during the study of zeeman effect. 'm' can have the (2l+1) values (-l,0,+l). Magnetic quantum number represents the orientation of atomic orbitals in three-dimensional space. the normal zeeman effect consists of the splitting of a spectral line of frequency $v_{0}$ into three components i.e.,
$v_{1} = v_{0} - \frac{e}{4 π m} B, v_{2} = v_{0}, V_{3} = v_{0} + \frac{e}{4 π m} B$
Here, B is magnetic field.
Q. Zeeman effect explains splitting of spectral lines is:View Solution
Question 28
The splitting of spectral lines by a magnetic field is called the zeeman effect after the Dutch physicist Pieter Zeeman. The Zeeman effect is a vivid confirmation of of space quantization. Magnetic quantum number 'm' was introduced during the study of zeeman effect. 'm' can have the (2l+1) values (-l,0,+l). Magnetic quantum number represents the orientation of atomic orbitals in three-dimensional space. the normal zeeman effect consists of the splitting of a spectral line of frequency $v_{0}$ into three components i.e.,
$v_{1} = v_{0} - \frac{e}{4 π m} B, v_{2} = v_{0}, V_{3} = v_{0} + \frac{e}{4 π m} B$
Here, B is magnetic field.
Q. In presence of magnetic field, d-suborbit is:View Solution
Question 29
Spin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum $= \sqrt{s (s + 1)} h$
Orbital angular momentum $= \sqrt{l (l + 1)} h$
Total spin of ana tom or ion is a multiple of $\frac{1}{2}$ . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity $= (2 \sum s + 1)$
Q. Total spin of $M n^{2 +} (Z = 25)$ ion will be:View Solution
Question 30
Spin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum $= \sqrt{s (s + 1)} h$
Orbital angular momentum $= \sqrt{l (l + 1)} h$
Total spin of ana tom or ion is a multiple of $\frac{1}{2}$ . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity $= (2 \sum s + 1)$
Q. Which of the following electronic configurations have four spin multiplicity?View Solution
Question 31
Spin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum $= \sqrt{s (s + 1)} h$
Orbital angular momentum $= \sqrt{l (l + 1)} h$
Total spin of ana tom or ion is a multiple of $\frac{1}{2}$ . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity $= (2 \sum s + 1)$
Q. Which of the following quantum numbers is not derived from schrodinger wave equations?View Solution
Question 32
Spin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum $= \sqrt{s (s + 1)} h$
Orbital angular momentum $= \sqrt{l (l + 1)} h$
Total spin of ana tom or ion is a multiple of $\frac{1}{2}$ . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity $= (2 \sum s + 1)$
Q. In any subshell, the maximum number of electrons having same value of spin quantum numbers is:View Solution
Question 33
Spin angular momentum of an electron has no analogue in classical mechanics. Howerver, it turns out that the treatment of spin angular momentum is closely analogous to the treatment of orbital angular momentum
Spin angular momentum $= \sqrt{s (s + 1)} h$
Orbital angular momentum $= \sqrt{l (l + 1)} h$
Total spin of ana tom or ion is a multiple of $\frac{1}{2}$ . Spin multiplicity is a factor to confirm the electronic configuration of an atom or ion.
Spin multiplicity $= (2 \sum s + 1)$
Q. The orbital angular momentum of a 2p-electron is:View Solution
Question 34
Dual nature of matter was proposed by de Broglie in 1923, it was experimentally verified by Davisson and Germer by diffraction experiment. Wave character of amtter has significance only for microscopic partiles. De Broglie wavelength or wavelength of matter wave can be calculated using the following relation:
$λ = \frac{h}{m v}$
Where, 'm' and 'v' are te mass and velocity of the particle. de Broglie hypothesis suggested that electron waves were being diffracted by the target, much as X-rays are diffracted by planes of atoms in the crystals.
Q. Planck's constant has same dimension as that of:View Solution
Question 35
Dual nature of matter was proposed by de Broglie in 1923, it was experimentally verified by Davisson and Germer by diffraction experiment. Wave character of amtter has significance only for microscopic partiles. De Broglie wavelength or wavelength of matter wave can be calculated using the following relation:
$λ = \frac{h}{m v}$
Where, 'm' and 'v' are te mass and velocity of the particle. de Broglie hypothesis suggested that electron waves were being diffracted by the target, much as X-rays are diffracted by planes of atoms in the crystals.
Q. Wave nature of electrons is shown by:View Solution
Question 36
Dual nature of matter was proposed by de Broglie in 1923, it was experimentally verified by Davisson and Germer by diffraction experiment. Wave character of amtter has significance only for microscopic partiles. De Broglie wavelength or wavelength of matter wave can be calculated using the following relation:
$λ = \frac{h}{m v}$
Where, 'm' and 'v' are te mass and velocity of the particle. de Broglie hypothesis suggested that electron waves were being diffracted by the target, much as X-rays are diffracted by planes of atoms in the crystals.
Q. de Broglie equation is obtained by combination of which of the following theories?View Solution
Question 37
Dual nature of matter was proposed by de Broglie in 1923, it was experimentally verified by Davisson and Germer by diffraction experiment. Wave character of amtter has significance only for microscopic partiles. De Broglie wavelength or wavelength of matter wave can be calculated using the following relation:
$λ = \frac{h}{m v}$
Where, 'm' and 'v' are te mass and velocity of the particle. de Broglie hypothesis suggested that electron waves were being diffracted by the target, much as X-rays are diffracted by planes of atoms in the crystals.
Q. Which among the following is not used to calculate the de Broglie wavelength?View Solution
Question 38
Dual nature of matter was proposed by de Broglie in 1923, it was experimentally verified by Davisson and Germer by diffraction experiment. Wave character of amtter has significance only for microscopic partiles. De Broglie wavelength or wavelength of matter wave can be calculated using the following relation:
$λ = \frac{h}{m v}$
Where, 'm' and 'v' are te mass and velocity of the particle. de Broglie hypothesis suggested that electron waves were being diffracted by the target, much as X-rays are diffracted by planes of atoms in the crystals.
Q. The wavelength of matter waves associated with a body of mass 1000 g moving with a velocity of 100 m/sec is:View Solution
Question 39
Dual nature of matter was proposed by de Broglie in 1923, it was experimentally verified by Davisson and Germer by diffraction experiment. Wave character of amtter has significance only for microscopic partiles. De Broglie wavelength or wavelength of matter wave can be calculated using the following relation:
$λ = \frac{h}{m v}$
Where, 'm' and 'v' are te mass and velocity of the particle. de Broglie hypothesis suggested that electron waves were being diffracted by the target, much as X-rays are diffracted by planes of atoms in the crystals.
Q. An electron microscope is used to probe the atomic arrangement to a resolution of 5Ã…. What should be the electric potential to which the electrons need to be accelerated?View Solution
Question 40
Orbital is the region in an atom where the probability of finding the electron around the nucleus. Orbitals do not specify a definite path according to the uncertainty principle. An orbital is described with the help of wave function $Φ$ . Whenever an electron is described by a wave function, we say that an electron occupies that orbital. Since, many wave functions are possible for an electron, there are many atomic orbitals in an atom. Orbitals have different shapes, except s-orbitals, all other orbitals hae different shapes, except s-orbitals, all other orbital have different shapes, except s-orbitals, all other orbitals have directional character. Number of spherical nodes in an orbital is equal to $(n - l - 1)$ . Orbital angular momentum of an electron is $\sqrt{l (l + 1)} h$ .
Q. Which of thef ollowing orbitals is not cylinderically symmetrical about z-axis?View Solution
Question 41
Orbital is the region in an atom where the probability of finding the electron around the nucleus. Orbitals do not specify a definite path according to the uncertainty principle. An orbital is described with the help of wave function $Φ$ . Whenever an electron is described by a wave function, we say that an electron occupies that orbital. Since, many wave functions are possible for an electron, there are many atomic orbitals in an atom. Orbitals have different shapes, except s-orbitals, all other orbitals hae different shapes, except s-orbitals, all other orbital have different shapes, except s-orbitals, all other orbitals have directional character. Number of spherical nodes in an orbital is equal to $(n - l - 1)$ . Orbital angular momentum of an electron is $\sqrt{l (l + 1)} h$ .
Q. The nodes present in 5p-orbital are:View Solution
Question 42
Orbital is the region in an atom where the probability of finding the electron around the nucleus. Orbitals do not specify a definite path according to the uncertainty principle. An orbital is described with the help of wave function $Φ$ . Whenever an electron is described by a wave function, we say that an electron occupies that orbital. Since, many wave functions are possible for an electron, there are many atomic orbitals in an atom. Orbitals have different shapes, except s-orbitals, all other orbitals hae different shapes, except s-orbitals, all other orbital have different shapes, except s-orbitals, all other orbitals have directional character. Number of spherical nodes in an orbital is equal to $(n - l - 1)$ . Orbital angular momentum of an electron is $\sqrt{l (l + 1)} h$ .
Q. When an atom is placed in a magnetic field, the possible number of orientations for an orbital of azimuthal quantum number 3 is:View Solution
Question 43
Orbital is the region in an atom where the probability of finding the electron around the nucleus. Orbitals do not specify a definite path according to the uncertainty principle. An orbital is described with the help of wave function $Φ$ . Whenever an electron is described by a wave function, we say that an electron occupies that orbital. Since, many wave functions are possible for an electron, there are many atomic orbitals in an atom. Orbitals have different shapes, except s-orbitals, all other orbitals hae different shapes, except s-orbitals, all other orbital have different shapes, except s-orbitals, all other orbitals have directional character. Number of spherical nodes in an orbital is equal to $(n - l - 1)$ . Orbital angular momentum of an electron is $\sqrt{l (l + 1)} h$ .
Q. Orbital angular momentum of f-electrons is:View Solution
Question 44
Orbital is the region in an atom where the probability of finding the electron around the nucleus. Orbitals do not specify a definite path according to the uncertainty principle. An orbital is described with the help of wave function $Φ$ . Whenever an electron is described by a wave function, we say that an electron occupies that orbital. Since, many wave functions are possible for an electron, there are many atomic orbitals in an atom. Orbitals have different shapes, except s-orbitals, all other orbitals hae different shapes, except s-orbitals, all other orbital have different shapes, except s-orbitals, all other orbitals have directional character. Number of spherical nodes in an orbital is equal to $(n - l - 1)$ . Orbital angular momentum of an electron is $\sqrt{l (l + 1)} h$ .
Q. Which of the following orbitals has/have two nodal planes?View Solution
Question 45
The hydrogen-like species $L i^{2 +}$ is in a spherically symmetric state $S_{1}$ with one radial node. Upon absorbing light the ion undergoes transition to a state $S_{2}$ . The state $S_{2}$ has one radial node and its energy is equal to the ground state energy of the hydrogen atom.
Q. The state $S_{1}$ is:View Solution
Question 46
The hydrogen -like species $L i^{2 +}$ is in a spherically symmetric state $S_{1}$ with one node. Upon absorbing light , the ion undergoes transition to a state $S_{2}$ . The state $S_{2}$ has one radial node and its energy is equal is to the ground state energy of the hydrogen atom.
Energy of the state $S_{1}$ in units of the hydrogen atom ground state energy is View Solution
Question 47
The hydrogen -like species $L i^{2 +}$ is in a spherically symmetric state $S_{1}$ with one node. Upon absorbing light , the ion undergoes transition to a state $S_{2}$ . The state $S_{2}$ has one radial node and its energy is equal is to the ground state energy of the hydrogen atom.
The orbital angular momentum quantum number of the state $S_{2}$ is View Solution
Question 48
According to the Bohr model, the energy levels of hydrogen atom can be found by making two assumptions.
(i). The electrons move in circulr orbit and (ii) the angular momentum of the electron in the $n^{t h}$ energy level is quantized to have a value $n \frac{h}{2 π}$ . The levels calculated with nuclear charge Ze, with a single electron in the orbit, are called Hydrogenic levels. Assume that the two electrons in the ground state of a helium atom occupy the corresponding lowest Hydrogenic level.
Q. The minimum repulsive energy between the two electrons would then be:View Solution
Question 49
According to the Bohr model, the energy levels of hydrogen atom can be found by making two assumptions.
(i). The electrons move in circulr orbit and (ii) the angular momentum of the electron in the $n^{t h}$ energy level is quantized to have a value $n \frac{h}{2 π}$ . The levels calculated with nuclear charge Ze, with a single electron in the orbit, are called Hydrogenic levels. Assume that the two electrons in the ground state of a helium atom occupy the corresponding lowest Hydrogenic level.
Q. if the hydrogen atom ionizatioin temperature is T, the temperature at which He atoms ionise completely (both electron having left the atom) would be:View Solution

All Exercises from G.R. BATHLA & SONS CHEMISTRY Class 11 CHEMISTRY ATOMIC STRUCTURE

Home
Ask Doubt
Profile