Problem from DHANPAT RAI & CO PHYSICS Chapter 20 ROTATIONAL MOTION for Class 11
| Class 11 | PHYSICS |
| Chapter | ROTATIONAL MOTION |
| DHANPAT RAI & CO PHYSICS | Problem |
| Medium | English |
| Academic Year | 2023-2024 |
Question 1
An isolated particle of mass m is moving in a horizontal plane (x-y), along the x-axis at a certain height above the ground. It suddenly explodes into two fragments of masses m/4 and 3m/4. At instant later, the smaller fragment is at y=+5cm. What is the position of larger fragment at this instant ?View SolutionQuestion 2
A small sphere of radius R is held against the inner surface of α larger sphere of radius 6R. The masses of large and small spheres are 4M and M, respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. find the co-ordinations of the centre of the larger sphere when the smaller sphere reaches the other extreme position.
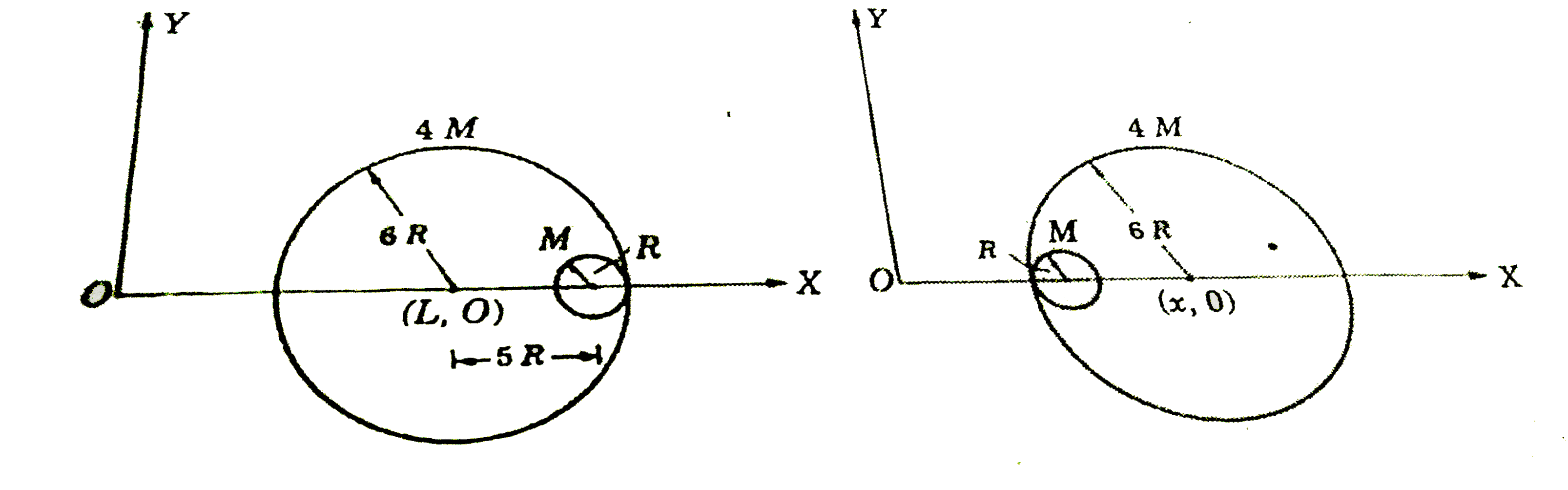 View Solution
View SolutionQuestion 4
A block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?
 View Solution
View SolutionQuestion 5
Two blocks of mass m1andm2 are connected to the ends of a spring. The spring is held compressed and the system is placed on a smooth horizontal table. The block of mass m1=2kg is kept at x=1cm mark and the other block is at x=2cm mark. The system is released from this position. It was observed that at the instant m1 was at x=5cm mark its velocity was zero and at that moment m2 was located at x=−4cm. Find mass m2 and unstretched length (l0) of the spring
 View Solution
View SolutionQuestion 15
A small block of mass m slides along a smooth track, as shown in fig. (i) If it starts from rest at P, what is the resulting force acting on it at Q ? (ii) at what height above the bottom of the loop should the block be released so that the force it exerts against the track at the top of the loop equals its weight?
 View Solution
View SolutionQuestion 16
Point masses m1 and m2 are placed at the ends of a rigid rod of length L and negligible mass. The rod is to be set rotating about an axis perpendicular to its length. Locate a point on the rod through which the axis of rotation should pass in order that the work required to set the rod rotating with angular velocity ω0 is minimum.View SolutionQuestion 17
A thin uniform bar lies on a frictionless horizontal surface and is free to move in any way on the surface. Its mass is 0.16 kg and lengths is √3m. Two particles, each of mass 0.08kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10ms−1 and the other with 6ms−1, as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distance 0.5 m from the centre of the bar. The particles strike the bar at same instant of time and stick to the bar on collision. Calculate the loss of kinetic energy of the system in the above collision process.
 View Solution
View SolutionQuestion 19
A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
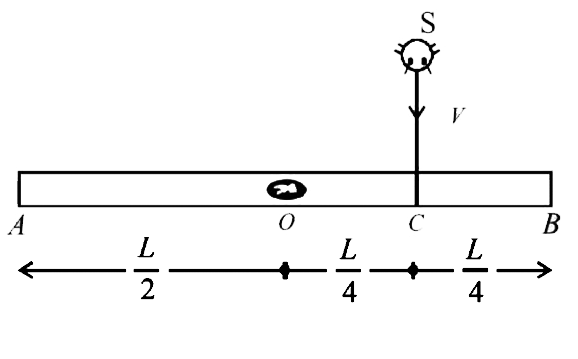 View Solution
View SolutionQuestion 20
A solid cylinder at rest at top of an inclined plane of height 2.7 m rolls down without slipping. If the same cylinder has to slide down a frictionless inclined plane and acquires the same velocity as that acquired by centre of mass of rolling cylinder at the bottom of the incline, what should be the height of inclined plane?View SolutionQuestion 21
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.View SolutionQuestion 23
A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part, The horizontal part, is 1.0 metre above the ground lenvel and the top of the track is 2.4 meters above the ground. Find the distance on the ground with respect to the point B (which is vertically below the end of the track as shown i fig.) where the sphere lands. During its flight as a projectlie, does the sphere continue to rotate about its centre of mass? Explain.
 View Solution
View SolutionQuestion 24
A thread is passing through a hole at the centre of frictionless table. At the upper end a block of mass 0.5kg is tied and a block of mass 8.0kg is tied at the lower end which is freely hanging. The smaller mass is rotate, on the table with a constant angular velocity about the axis passing through the hole so as to balance the heavier mass. If the mass of the hanging block is changed from 8.0kg to 1.0kg, what is the fractional change in the radius and the angular velocity of the smaller mass so that it balances the hanging mass again?
 View Solution
View Solution
