JEE MAINS & ADVANCED MATHS (HINDI) अध्याय 181:JEE ADVANCED सोल्वड पेपर्स 2018 की पेपर 2 (खण्ड 1 ) कक्षा 12 के लिए
| कक्षा 12 | गणित |
| Chapter | JEE ADVANCED सोल्वड पेपर्स 2018 |
| JEE MAINS & ADVANCED MATHS (HINDI) | पेपर 2 (खण्ड 1 ) |
| माध्यम | हिंदी |
| शैक्षणिक वर्ष | 2023-2024 |
Question 1
किसी भी धनात्मक पूर्णांक (positive integer n) के लिए,
fn:(0,∞)→R
fn(x)=n∑j=1tan−1(11+(x+j)(x+j−1)) सभी x∈(0,∞) के लिए, के द्वारा परिभाषित है| (यहाँ प्रतिलोम त्रिकोणमितीय फलन (inverse trignometric function) tan−1x,(−π2,π2) में मान धारण करता है)| तब निम्नलिखित में से कौन सा (से) कथन सत्य है (हैं)? हल देखेंQuestion 2
माना की T, बिंदुओं P(−2,7) और Q(2,−5) से गुजरने वाली रेखा (line) है| माना की F1 उन सभी वृत्त युग्मों (pairs of circles) (S1,S2) का सम्मुच्य (set) है रेखा T, S1 के बिंदु P पर और S2 के बिंदु Q पर स्पर्शी (tangent) है तथा वृत्त S1 व S2 एक दूसरे को बिंदु माना की M, पर स्पर्श करते है| जब युग्म (S1,S2),F1 में विचरित (varies) करता है तो माना की सम्मुच्चय (set) E1 बिंदु M के बिन्दुपथ को दर्शाता है| माना की F2 उन सरल रेखा-खण्डों का सम्मुच्य है जो बिंदु R(1,1) से गुजरती है तथा E1 के दो भिन्न बिंदुओं के युग्म को जोड़ती है| माना की E2 सम्मुच्य F2 के रेखाख़ण्डों के मध्य बिंदुओं का सम्मुच्य है| तब निम्नलिखित में से कौन सा (से) कथन सत्य है? हल देखेंQuestion 3
माना की S उन सभी स्तम्भ आव्यूहों ⎡⎢⎣b1b2b3⎤⎥⎦का समुच्चय है जिनके लिए b1,b2,b3∈R और वास्तविक चरो
−x+2y+5z=b1
2x−4y+3z=b2
x−2y+2z=b3 वाले समीकरण निकाय का कम से कम एक हल है। तब निम्नलिखित वास्तविक चरो वाले निकायों में से किस (कौन से ) निकाय (निकाय ) का भी प्रत्येक ⎡⎢⎣b1b2b3⎤⎥⎦∈S के लिए कम से कम एक हल है ?हल देखेंQuestion 4
ऐसी दो सरल रेखाओं पर विचार कीजिए, जिनमें से प्रत्येक वृत्त x2+y2=12 और परवलय y2=4x दोनों पर ही स्पर्शी है | माना कि ये रेखाएं बिन्दु Q पर प्रतिछेद करती है | एक ऐसी दीर्घवृत्त पर विचार कीजिये जिसका केन्द्र मूलबिंदु O(0,0) पर है और जिसका अर्ध - दीर्घ अक्ष O Q है | यदि इस दीर्घवृत्त के लघु अक्ष की लम्बाई √2 है, तब निम्नलिखित में से कौन सा (से) कथन सत्य है (हैं) हल देखेंQuestion 12
माना कि P प्रथ्म अष्ठांश में एक बिंदु है जिसका समतल x+y=3 में प्रतिबिम्ब Q (अर्थात रेखाखण्ड PQ समतल x+y=3 के लम्बवत है और PQ का मध्य बिंदु समतल x+y=3 में स्थित है)z- अक्ष पर स्थित है । माना कि P की x- अक्ष से दूरी 5 है। यदि P का xy- समतल में प्रतिबिम्ब R है तब PR की लमबाई है-----------हल देखेंQuestion 13
प्रथम अष्टांश में एक ऐसे घन पर विचार कीजिए, जिसकी भुजाओं OP, OQ और OR की लम्बाई 1 है और जो क्रमश: x-अक्ष, y-अक्ष और z-अक्ष के अनुदिश हैं, जहाँ O(0,0,0) मूलबिन्दु है | मना कि घन का केन्द्र S(12,12,12) है, शीर्ष T मूलबिन्दु O के सम्मुख वाला वह शीर्ष है कि बिन्दु S विकर्ण OT पर स्थित है | यदि →p=−→SP,→q=−−→SQ,→r=−−→SR और →t=−→ST, तब ∣∣(→p×→q)×(→r×→t)∣∣ का मान है हल देखेंQuestion 15
माना की E1={x∈R:x≠1औरxx−1>0} और E2={x∈E1sin−1(loge(xx−1)} एक वास्तविक संख्या (real number) है|
(यहाँ प्रतिलोम त्रिकोणमितीय फलां (inverse trignometric function) sin−1x,[−π2,π2] में मान धारण करता है|
माना की फलन: f:E1→R,f(x)=loge(xx−1) के द्वारा परिभाषित है
और फलन f:E2→R,g(x)=sin−1lloge(xx−1) के द्वारा परिभाषित है|

दिए हुए विकल्पों में से सही विकल्प है हल देखेंQuestion 16
एक हाई स्कूल (high school) में, 6 बालकों M1,M2,M3,M4,M5,M6 और 5 बालिकाओं G1,G2,G3,G4,G5, के समूह (group) में से एक समिति (committee) बनाई जानी है। (i) माना कि α1 समिति को इस प्रकार से बनाने के तरीकों (ways) की कुल संख्या है कि समिति में 5 सदस्य हैं, जिनमें से ठीक (exactly) 3 बालक और 2 बालिकाएँ हैं। (ii) माना कि α2 समिति को इस प्रकार से बनाने के तरीकों की कुल संख्या है कि समिति में कम से कम (atleast) 2 सदस्य हैं, और बालकों और बालिकाओं की संख्या बराबर (equal) है। (iii) माना कि α3 समिति को इस प्रकार से बनाने के तरीकों की कुल संख्या है कि समिति में 5 सदस्य हैं, जिनमें से कम से कम 2 बालिकाएँ हैं। (iv) माना कि α4 समिति को इस प्रकार से बनाने के तरीकों की कुल संख्या है कि समिति में 4 सदस्य हैं, जिनमें से कम से कम 2 बालिकाएँ हैं और M1 व G1 समिति में एक साथ नहीं हैं।

दिए हुए विकल्पों में से सही विकल्प है:हल देखेंQuestion 17
माना कि H : x2a2−y2b2=1 , जहाँ a>b>0,xy समतल (plane) में एक ऐसा अतिपरवलय (hyperbola) है जिसका संयुग्मी अक्ष (conjugateaxis) LM उसके एक शीर्ष (vertex)N पर 60∘ का कोण (angle) अंतरित (subtend) करता है। माना कि त्रिभुज (triangle) LMN का क्षेत्रफल (area) 4√3 है।
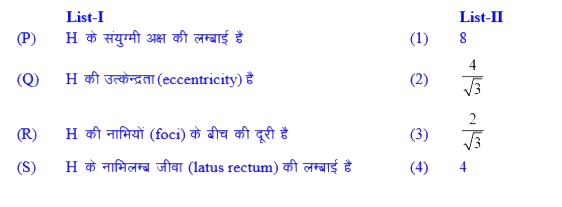
दिए हुए विकल्पों में से सही विकल्प है हल देखेंQuestion 18
माना कि फलन
f1:R→R,f2:(−π2,π2)→R,f3:(−1,eπ2−2)→R और f4:R→R इस प्रकार परिभाषित है कि
(i) f1(x)=sin(√1−e−x2),
(ii) f2(x)={|sinx|tan−1xifx≠01ifx=0 जहां प्रतिलोम त्रिकोणमितीय फलन tan−1x,(−π2,π2) में मान धारण करता है
(iii) f3(x)=[sin(loge(x+2))], जहां tεR के लिए [t],t से छोटा या t के बराबर महत्तम पूर्णांक को दर्शाता है।
(iv) f4(x)=⎧⎨⎩x2sin(1x)यदिx≠0xयदिx=0
 हल देखें
हल देखें