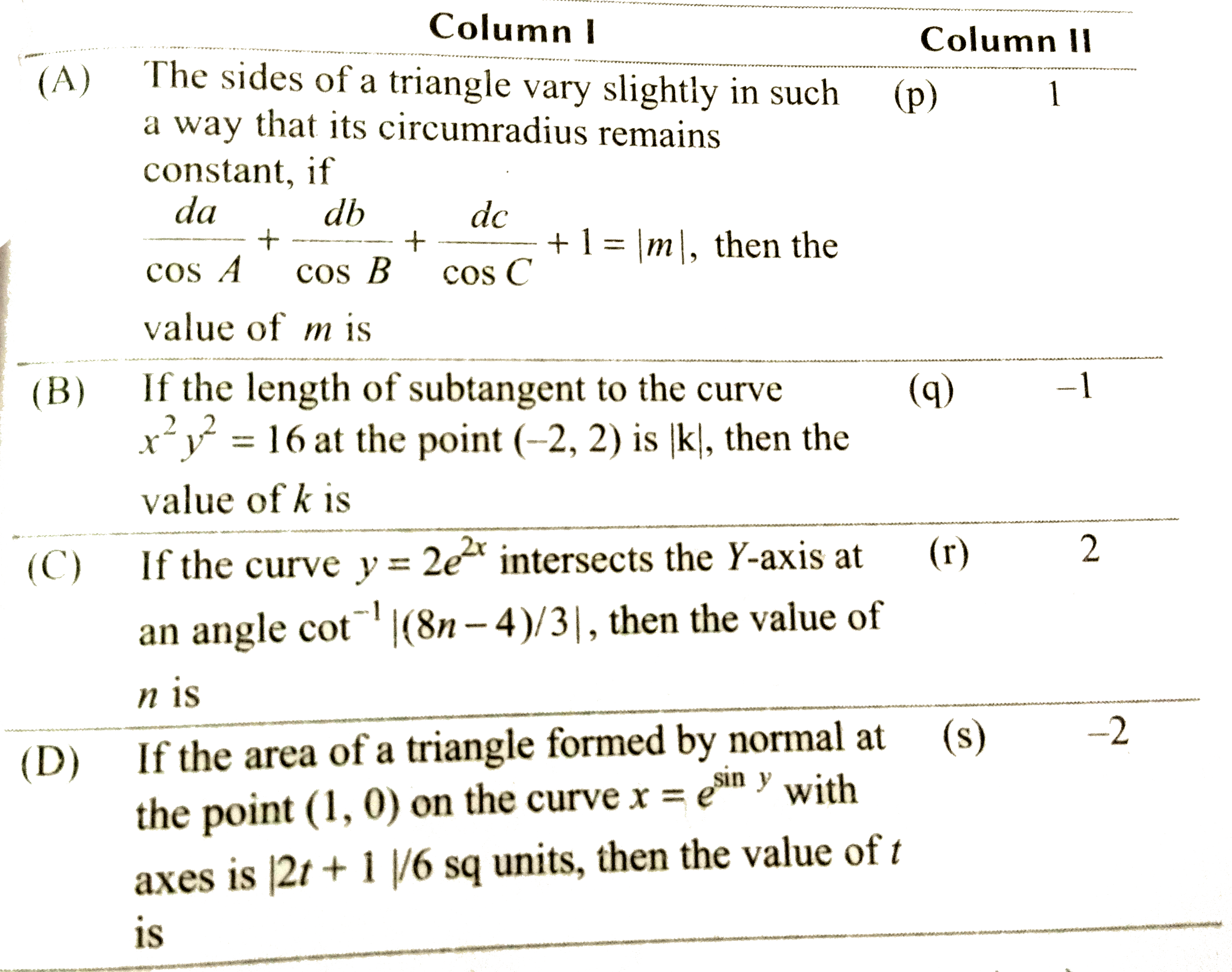Examples from ARIHANT MATHS (ENGLISH) MONOTONICITY MAXIMA AND MINIMA for Class 12
| Class 12 | MATHS |
| Chapter | MONOTONICITY MAXIMA AND MINIMA |
| ARIHANT MATHS (ENGLISH) | Examples |
| Medium | English |
| Academic Year | 2023-2024 |
Question 11
Consider the ellipse x2f(k2+2k+5)+y2f(k+11)=1. If f(x) is a positive decr4easing function, then the set of values of k for which the major axis is the x-axis is (−3,2). the set of values of k for which the major axis is the y-axis is (−∞,2). the set of values of k for which the major axis is the y-axis is (−∞,−3)∪(2,∞) the set of values of k for which the major axis is the y-axis is (−3,−∞,)View SolutionQuestion 69
A solid cylinder of height H has a conical portion of same height and radius 1/3rd of height removed from it.
Rain water is accumulating in it, at the rate equal to π times the instaneous radius of the water surface inside the hole, the time after which hole will filled with water is View SolutionQuestion 70
If composite function f1(f2(f3((fn(x))))n timesis an decreasing function and if 'r' functions out of total 'n' functions are decreasing function while rest are increasing, then the maximum value of r(n−r) is (a) n2−44 , when n is of the form 4k (b) n24, when n is an even number (c) n2−14, when n is an odd number (d) n24, when n is of the form 4k+2View SolutionQuestion 78
Statement I :Among all the rectangles of the given perimeter, the square has the largest area. Also among all the rectangles of given area, the square has the least perimeter.
Statement II :For x>0,y>0,ifx+y= constant, then xy will be maximum for y=x and if xy=constant, then x+y will be minimum for y=x.View SolutionQuestion 86
Consider a ΔOAB formed by the point O(0,0),A(2,0),B(1,√3).P(x,y) is an arbitrary interior point of triangle moving in such a way that d(P,OA)+d(P,AB)+d(P,OB)=√3, where d(P,OA),d(P,AB),d(P,OB) represent the distance of P from the sides OA,AB and OB respectively
Area of region reperesenting all possible position of point P is equal to View SolutionQuestion 90
The absolute maximum and minimum values of functions can be found by their monotonic and asymptotic behaviour provided they exist. We may agree that finite limits values may be reagarded as absolute maximum or minimum. For instance the absolute maximum value of 11+x2 is unity. It is attained at x=0 while absolute maximum value of the same functions is zero which is a limiting value of (x→∞orx→−∞)
The function x4−4x+1 will have.View SolutionQuestion 91
The absolute maximum and minimum values of functions can be found by their monotonic and asymptotic behaviour provided they exist. We may agree that finite limits values may be reagarded as absolute maximum or minimum. For instance the absolute maximum value of 11+x2 is unity. It is attained at x=0 while absolute maximum value of the same functions is zero which is a limiting value of (x→∞orx→−∞)
The absolute minimum value of the function x−2√x2+1 is View SolutionQuestion 92
The absolute maximum and minimum values of functions can be found by their monotonic and asymptotic behaviour provided they exist. We may agree that finite limits values may be reagarded as absolute maximum or minimum. For instance the absolute maximum value of 11+x2 is unity. It is attained at x=0 while absolute maximum value of the same functions is zero which is a limiting value of (x→∞orx→−∞)
The absolute minimum and maximum values of the function x2−x+1x2+x+1 is View SolutionQuestion 93
The absolute maximum and minimum values of functions can be found by their monotonic and asymptotic behaviour provided they exist. We may agree that finite limits values may be reagarded as absolute maximum or minimum. For instance the absolute maximum value of 11+x2 is unity. It is attained at x=0 while absolute maximum value of the same functions is zero which is a limiting value of (x→∞orx→−∞)
The function x4−4x+1 will have.View SolutionQuestion 94
The absolute maximum and minimum values of functions can be found by their monotonic and asymptotic behaviour provided they exist. We may agree that finite limits values may be reagarded as absolute maximum or minimum. For instance the absolute maximum value of 11+x2 is unity. It is attained at x=0 while absolute maximum value of the same functions is zero which is a limiting value of (x→∞orx→−∞)
The function x4−4x+1 will have.View SolutionQuestion 95
We are given the curvers y=∫x−∞f(t)dt through the point (0,12) any y=f(x), where f(x)>0andf(x) is differentiable ,∀x∈ R through (0,1) Tangents drawn to both the curves at the points with equal abscissae intersect on the same point on the X- axists
The number of solutions f(x)=2ex is equal to View SolutionQuestion 106
If a function (continuos and twice differentiable) is always concave upward in an interval, then its graph lies always below the segment joining extremities of the graph in that interval and vice-versa.
Let f:R+→R+ is such that f(x)≥0∀x∈[a,b]. Then value of ∫baf(x)dx cannot exceed:View SolutionQuestion 113
The radius of a right circular cylinder increases at a constant rate. Its altitude is a linear function of the radius and increases three times as fast as the radius when the radius is 1 cm and the altitude is 6 cm. When the radius is 6cm, the volume is increasing at the rate of 1 cm3s . When the radius is 36cm, the volume is increasing at a rate of n cm3s. What is the value of n?View SolutionQuestion 132
Sohan has x children by his first wife. Geeta has (x+1) children by her first husband. The marry and have children of their own. The whole family has 24 children. Assuming that two children of the same parents do not fight, prove that the maximum possible number of fights that can take place is 191.View SolutionQuestion 151
A window of perimeter P (including the base of the arch) is in the form of a rectangle surrounded by a semi-circle. The semi-circular portion is fitted with the colored glass while the rectangular part is fitted with the clear glass that transmits three times as much light per square meter as the colored glass does. What is the ratio for the sides of the rectangle so that the window transmits the maximum light?View SolutionQuestion 159
From point A located on a highway as shown in figure, one has to get by car as soon as possible to point B located in the field at a distance l from the highway. It is known that the car moves in the field time slower on the highway. At what distance from point D one must turn off the highway?
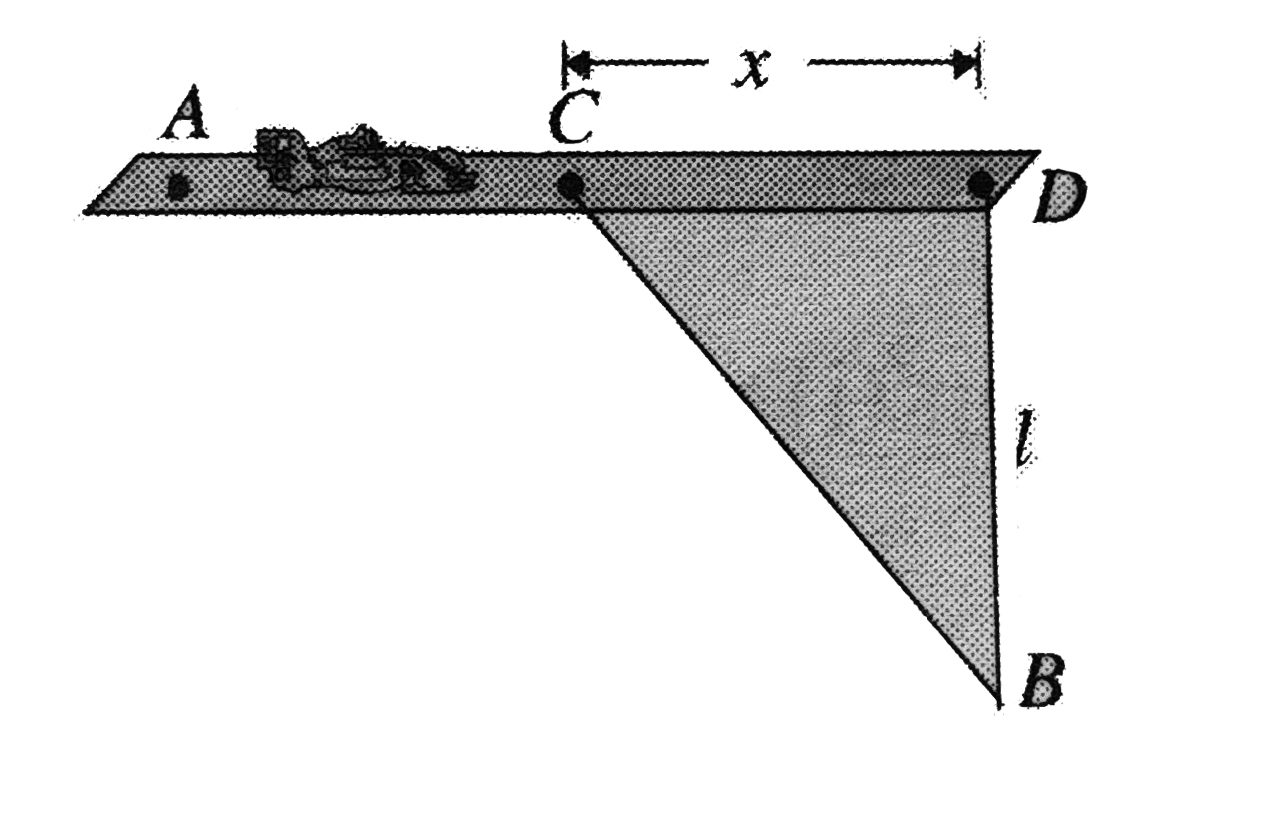View Solution
All Exercises from ARIHANT MATHS (ENGLISH) Class 12 MATHS MONOTONICITY MAXIMA AND MINIMA
- EXERCISE FOR SESSION 1
- EXERCISE FOR SESSION 2
- EXERCISE FOR SESSION 3
- EXERCISE FOR SESSION 4
- EXERCISE FOR SESSION 5
- EXERCISE (SINGLE OPTION CORRECT TYPE QUESTIONS)
- MAXIMA AND MINIMA EXERCISE 1
- EXERCISE (MORE THAN ONE CORRECT OPTION TYPE QUESTIONS)
- EXERCISE (STATEMENT I AND II TYPE QUESTIONS)
- EXERCISE (PASSAGE BASED QUESTIONS)
- MAXIMA AND MINIMA EXERCISE 4
- MAXIMA AND MINIMA EXERCISE 5
- EXERCISE (SINGLE INTEGER ANSWER TYPE QUESTIONS)
- MAXIMA AND MINIMA EXERCISE 6
- EXERCISE (QUESTIONS ASKED IN PREVIOUS 13 YEARS EXAM)
- EXAMPLE
- EXAMPLES