Examples from ARIHANT MATHS (ENGLISH) AREA OF BOUNDED REGIONS for Class 12

Class 12	MATHS
Chapter	AREA OF BOUNDED REGIONS
ARIHANT MATHS (ENGLISH)	Examples
Medium	English
Academic Year	2023-2024

Question 1
Mark the region represtented by $3 x + 4 y \leq 12$ .View Solution
Question 2
Sketch the curve $y = x^{3}$ .View Solution
Question 3
Sketch the curve $y = x^{3} - 4 x$ .View Solution
Question 4
Sketch the curve $y = (x - 1) (x - 2) (x - 3)$ .View Solution
Question 5
Sketch the graph for $y = x^{2} - x$ .View Solution
Question 6
Sketch the curve $y = sin 2 x$ .View Solution
Question 7
Sketch the curve $y = {sin}^{2} x$ .View Solution
Question 8
Construct the graph for $f (x) = \frac{x^{2} - 1}{x^{2} + 1}$ .View Solution
Question 9
Construct the graph for $f (x) = x + \frac{1}{x}$ .View Solution
Question 10
Construct the graph for $f (x) = \frac{1}{1 + e^{1 / x}}$ .View Solution
Question 11
Sketch the graph $y = | x + 1 | .$ Evaluate $\int_{- 4}^{2} | x + 1 | d x .$ What does the value of this integral represent on the graph?View Solution
Question 12
The area inside the parabola $5 x^{2} - y = 0$ but outside the parabola $2 x^{2} - y + 9 = 0$ is (a) $12 \sqrt{3}$ sq units (b) $6 \sqrt{3}$ sq units (c) $8 \sqrt{3}$ sq units (d) $4 \sqrt{3}$ sq units View Solution
Question 13
The area enclosed by $y = x (x - 1) (x - 2)$ and x-axis, is given by View Solution
Question 14
The area between the curve $y = 2 x^{4} - x^{2},$ the axis, and the ordinates of the two minima of the curve is 11/60 sq. units (b) 7/120 sq. units 1/30 sq. units (d) 7/90 sq. units View Solution
Question 15
Sketch the curves and identify the region bounded by the curves $x = \frac{1}{2}, x = 2, y = log x a n y = 2^{x} .$ Find the area of this region.View Solution
Question 16
Find the area of region : ${(x, y) : 0 \leq y \leq x^{2} + 1, 0 \leq y \leq x + 1, 0 \leq x \leq 2}$ .View Solution
Question 17
The area common to the region determined by $y \geq \sqrt{x}$ and $x^{2} + y^{2} < 2$ has the value View Solution
Question 18
Find the area of the figure enclosed by the curve $5 x^{2} + 6 x y + 2 y^{2} + 7 x + 6 y + 6 = 0 .$ View Solution
Question 19
If $f (x) = {\begin{matrix} \sqrt{{x}} & x \notin Z 1 & x \in Z \end{matrix}$ and $g (x) = {x}^{2}$ then area bounded by f(x) and g(x) for $x \in [0, 10]$ is View Solution
Question 20
Find the area of the region bounded by the curves $y = x^{2}, y = ∣ ∣ 2 - x^{2} ∣ ∣, and y = 2,$ which lies to the right of the line x=1.View Solution
Question 21
The area enclosed by the curve $| y | = sin 2 x,$ where $x \in [0, 2 π] .$ is View Solution
Question 22
Let $f (x) = x^{2}, g (x) = cos x$ and $α, β (α < β)$ be the roots of the equation $18 x^{2} - 19 π x + π^{2} = 0$ . Then the area bounded by the curves $u = fog (x)$ , the ordinates $x = α, x = β$ and the X-asis is View Solution
Question 23
Find the area bounded by the curves $x^{2} + y^{2} = 25, 4 y = ∣ ∣ 4 - x^{2} ∣ ∣,$ and $x = 0$ above the x-axis.View Solution
Question 24
Find area enclosed by $| x | + | y | = 1$ .View Solution
Question 25
Let $f (x) = max {sin x, cos x, \frac{1}{2}}$ , then determine the area of region bounded by the curves $y = f (x)$ , X-axis, Y-axis and $x = 2 π$ .View Solution
Question 26
If A denotes the area bounded by $f (x) = ∣ ∣ ∣ \frac{sin x + cos x}{x} ∣ ∣ ∣$ , X-axis, $x = π$ and $x = 3 π$ ,then View Solution
Question 27
If $y = f (x)$ makes positive intercepts of 2 and 1 unit on x and y-coordinates axes and encloses an area of $\frac{3}{4}$ sq unit with the axes, then $\int_{0}^{2} x f' (x) d x$ , is View Solution
Question 28
The area of the region included between the regions satisfying $min (| x |, | y |) \geq 1$ and $x^{2} + y^{2} \leq 5$ is View Solution
Question 29
The area of the region bounded by the curves $y = \sqrt{\frac{1 + sin x}{cos x}}$ and $y = \sqrt{\frac{1 - sin x}{cos x}}$ bounded by the lines x=0 and $x = \frac{π}{4}$ is View Solution
Question 30
Let T be the triangle with vertices $(0, 0), (0, c^{2}) and (c, c^{2})$ and let R be the region between $y = c x and y = x^{2}$ where $c > 0$ then View Solution
Question 31
Suppose fis defined from $R \to [- 1, 1]$ as $f (x) = \frac{x^{2} - 1}{x^{2} + 1}$ where R is the set of real number .then the statement which does not hold is View Solution
Question 32
Consider $f (x) = ⎧ ⎪ ⎨ ⎪ ⎩ \begin{matrix} cos x & 0 \leq x < \frac{π}{2} {(\frac{π}{2} - x)}^{2} & \frac{π}{2} \leq x < π \end{matrix}$ such that f is periodic with period $π$ . Then which of the following is not true?View Solution
Question 33
Consider the functions f(x) and g(x), both defined from $R \to R$ and are defined as $f (x) = 2 x - x^{2} and g (x) = x^{n}$ where $n \in N$ . If the area between f(x) and g(x) is 1/2, then the value of n is View Solution
Question 34
The area of the region bounded by the curve $y = e^{x}$ and lines $x = 0 a n d y = e$ is $e - 1$ (b) $\int_{1}^{e} 1 n (e + 1 - y) d y$ $e - \int_{0}^{1} e^{x} d x$ (d) $\int_{1}^{e} 1 n y d y$ View Solution
Question 35
Consider the function $f (x) = x^{3} - 8 x^{2} + 20 x - 13$
The function $f (x)$ defined for $R \to R$ View Solution
Question 36
Consider the function $f (x) = x^{3} - 8 x^{2} + 20 x - 13$
Area enclosed by $y = f (x)$ and the coordinate axes is View Solution
Question 37
Let $h (x) - f (x) - g (x)$ where $f (x) = {sin}^{4} π x and g (x) = I n x$ . Let $x_{0}, x_{1}, x_{2}, ... ..., x_{n - 1}$ be the roots of $f (x) = g (x)$ in increasing oder.Then the absolute area enclosed by $y = f (x) and y = g (x)$ is given by View Solution
Question 38
Let $h (x) = f (x) = f_{x} - g_{x}$ , where $f_{x} = {sin}^{4} π x$ and $g (x) = I n x$ . Let $x_{0}, x_{1}, x_{2}, ... ., x_{n + 1}$ be the roots of $f_{x} = g_{x}$ in increasing order.
In the above question, the value of n is View Solution
Question 39
Let $h (x) = f (x) = f_{x} - g_{x}$ , where $f_{x} = {sin}^{4} π x$ and $g (x) = I n x$ . Let $x_{0}, x_{1}, x_{2}, ... ., x_{n + 1}$ be the roots of $f_{x} = g_{x}$ in increasing order.
The absolute area enclosed by $y = f_{x}$ and $y = g (x)$ is given by View Solution
Question 40
Consider the function defined implicitly by the equation $y^{3} - 3 y + x = 0$ on various intervals in the real line. If $x \in (- \infty, - 2) \cup (2, \infty)$ , the equation implicitly defines a unique real-valued defferentiable function $y = f (x)$ . If $x \in (- 2, 2)$ , the equation implicitly defines a unique real-valud diferentiable function $y - g (x)$ satisfying $g_{0} = 0$ .
If $f (- 10 \sqrt{2}) = 2 \sqrt{2}$ , then $f (- 10 \sqrt{2})$ is equal to View Solution
Question 41
Consider the function defined implicitly by the equation $y^{3} - 3 y + x = 0$ on various intervals in the real line. If $x \in (- \infty, - 2) \cup (2, \infty)$ , the equation implicitly defines a unique real-valued defferentiable function $y = f (x)$ . If $x \in (- 2, 2)$ , the equation implicitly defines a unique real-valud diferentiable function $y - g (x)$ satisfying $g_{0} = 0$ .
The area of the region bounded by the curve $y = f (x)$ , the X-axis and the line $x = a$ and $x = b$ , where $- \infty < a < b < - 2$ is View Solution
Question 42
Consider the function defined implicitly by the equation $y^{3} - 3 y + x = 0$ on various intervals in the real line. If $x \in (- \infty, - 2) \cup (2, \infty)$ , the equation implicitly defines a unique real-valued defferentiable function $y = f (x)$ . If $x \in (- 2, 2)$ , the equation implicitly defines a unique real-valud diferentiable function $y - g (x)$ satisfying $g_{0} = 0$ .
If $f (- 10 \sqrt{2}) = 2 \sqrt{2}$ , then $f (- 10 \sqrt{2})$ is equal to View Solution
Question 43
A curve $y = f (x)$ passes through point $P (1, 1)$ . The normal to the curve at $P$ is a $(y - 1) + (x - 1) = 0$ . If the slope of the tangent at any point on the curve is proportional to the ordinate of the point, then the equation of the curve is (a) $(b) (c) y = (d) e^{(e) (f) K ((g) (h) x - 1 (i)) (j)} (k) (l)$ (m) (b) $(n) (o) y = (p) e^{(q) (r) K e (s)} (t) (u)$ (v) (c) $(d) (e) y = (f) e^{(g) (h) K ((i) (j) x - 2 (k)) (l)} (m) (n)$ (o) (d) None of these View Solution
Question 44
Sketch the region bounded by the curves $y = x^{2} a n d y = \frac{2}{1 + x^{2}}$ . Find the area.View Solution
Question 45
The area enclosed between the curves $y = {log}_{e} (x + e), x = {log}_{e} (\frac{1}{y})$ , and the x-axis is View Solution
Question 46
Find the area of the region bounded by the curve C : y=tan x ,tangent drawn to C at x=pi/4, and the x-axis.View Solution
Question 47
Find all the possible values of $b > 0,$ so that the area of the bounded region enclosed between the parabolas $y = x - b x^{2} a n d y = \frac{x^{2}}{b}$ is maximum.View Solution
Question 48
Let $C_{1} and C_{2}$ be the graphs of the functions $y = x^{2} and y = 2 x,$ respectively, where $0 \leq x \leq 1 . Let C_{3}$ be the graph of a function y=f(x), where $0 \leq x \leq 1, f (0) = 0 .$ For a point P on $C_{1},$ let the lines through P, parallel to the axes, meet $C_{2} and C_{3}$ at Q and R, respectively (see figure). If for every position of $P (o n C_{1}),$ the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View Solution
Question 49
Compute the area of the region bounded by the curves $y - e x {(log)}_{e} x a n d y = \frac{log x}{e x}$ View Solution
Question 50
If $A_{n}$ be the area bounded by the curve $y = {(tan x)}^{n}$ and the lines $x = 0, y = 0, x = π / 4$ , then for $n > 2 .$ View Solution
Question 51
Consider a square with vertices at $(1, 1), (- 1, 1), (- 1, - 1) and (1, - 1)$ . Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area. View Solution
Question 52
The area of the region included between the curves $x^{2} + y^{2} = a^{2} and \sqrt{| x |} + \sqrt{| y |} = \sqrt{a} (a > 0)$ is View Solution
Question 53
Show that the area included between the parabolas $y^{2} = 4 a (x + a) and y^{2} = 4 b (b - x)$ is $\frac{8}{3} \sqrt{a b} (a + b) .$ View Solution
Question 54
Determine the area of the figure bounded by two branches of the curve ${(y - x)}^{2} = x^{3}$ and the straight line $x = 1$ .View Solution
Question 55
Prove that the areas $S_{0}, S_{1}, S_{2}$ ...bounded by the $x$ -axis and half-waves of the curve $y = e^{- a x} sin β x, x \geq 0$ form a geometric progression with the common ratio $r = e^{- π α / β}$ .View Solution
Question 56
Let $b \neq 0$ and for $j = 0, 1, 2, ... ., n$ . Let $S_{j}$ be the area of the region bounded by Y_axis and the curve $x \cdot e^{a y} = sin b y, \frac{j π}{b} \leq y \leq \frac{(j + 1) π}{b}$ . Show that $S_{0}, S_{1}, S_{2}, ... S_{n}$ are in geometric progression. Also, find their sum for a=-1 and $b = π$ .View Solution
Question 57
For any real $t, x = \frac{1}{2} (e^{t} + e^{- t}), y = \frac{1}{2} (e^{t} - e^{- t})$ is a point on the hyperbola $x^{2} - y^{2} = 1$ Show that the area bounded by the hyperbola and the lines joining its centre to the points corresponding to $t_{1} a n d - t_{1}$ is $t_{1} .$ View Solution
Question 58
Find the area enclosed by circle $x^{2} + y^{2} = 4$ , parabola $y = x^{2} + x + 1$ , the curve $y = [\frac{{sin}^{2} x}{4} + \frac{cos x}{4}]$ and X-axis (where,[.] is the greatest integer function.View Solution
Question 59
Let $f (x) = M a ξ μ m {x^{2}, {(1 - x)}^{2}, 2 x (1 - x)},$ where $0 \leq x \leq 1 .$ Determine the area of the region bounded by the curves $y = f (x), x - a ξ s, x = 0,$ and $x = 1 .$ View Solution
Question 60
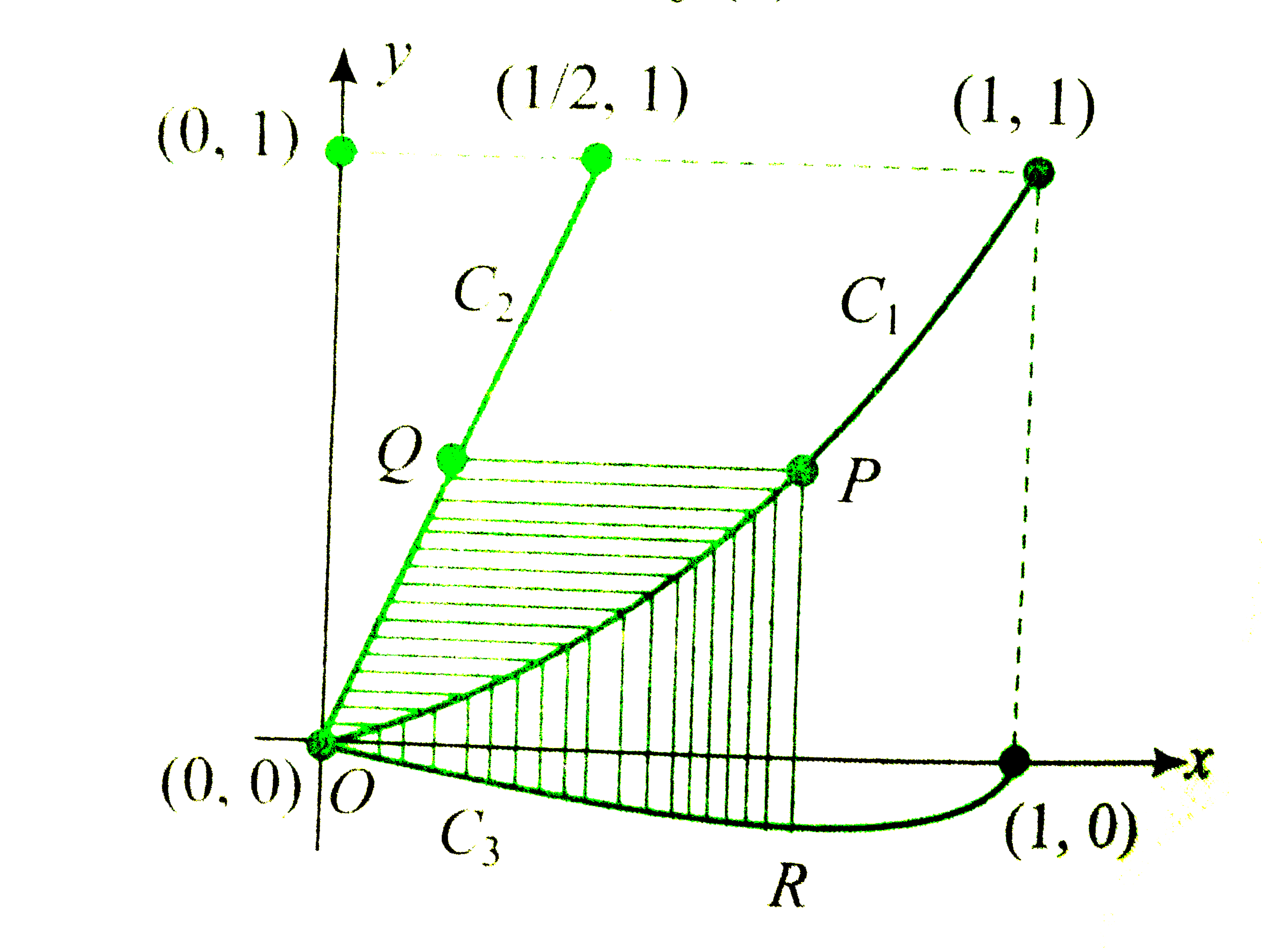Let $f (x) = {\begin{matrix} - 2 & - 3 \leq x \leq 0 x - 2 & 0 < x \leq 3 \end{matrix}$ , where $g (x) = min {f (| x |) + | f (x) |, f (| x |) - | f (x) |}$ . Find the area bounded by the curve $g (x)$ and the X-axis between the ordinates at $x = 3$ and $x = - 3$ .View Solution
Question 61
Let $O (0, 0), A (2, 0), a n d B (1 \frac{1}{\sqrt{3}})$ be the vertices of a triangle. Let $R$ be the region consisting of all those points $P$ inside $O A B$ which satisfy $d (P, O A) \leq min [d (p, O B), d (P, A B)]$ , where $d$ denotes the distance from the point to the corresponding line. Sketch the region $R$ and find its area.View Solution
Question 62
A curve $y = f (x)$ passes through the origin. Through any point $(x, y)$ on the curve, lines are drawn parallel to the co-ordinate axes. If the curve divides the area formed by these lines and co-ordinates axes in the ratio $m : n,$ find the curve.View Solution
Question 63
Find the ratio of the areas in which the curve $y = [\frac{x^{3}}{100} + \frac{x}{35}]$ divides the circle $x^{2} + Y^{2} - 4 x + 2 y + 1 = 0$ . (where, [.] denotes the greated integer function).View Solution
Question 64
Area bounded by the line y=x, curve $y = f (x), (f (x) > x, \forall x > 1)$ and the lines x=1,x=t is $(t - \sqrt{1 + t^{2}} - (1 + \sqrt{2}))$ for all $t > 1$ . Find $f (x)$ .View Solution
Question 65
If the area bounded by the curve y=f(x), x-axis and the ordinates x=1 and x=b is (b-1) $sin$ (3b+4), then find f(x).View Solution
Question 66
Let f (x) be a function which satisfy the equatio $f (x y) = f 9 x) + f (y)$ for all $x > 0, y > 0$ such that $f' (1) = 2 .$ Let A be the area of the region bounded by the curves $y = f (x), y = ∣ ∣ x^{3} - 6 x^{2} + 11 x - 6 ∣ ∣ and x = 0,$ then find value of $\frac{28}{17} A .$ View Solution
Question 67
Find the area of the region which is inside the parabola satisfying the condition $| x - 2 y | + | x + 2 y | \leq 8$ and $x y \geq 2$ . View Solution
Question 68
Consider the function $f (x) = {\begin{matrix} x - [x] - \frac{1}{2} & x \notin 0 & x \in I \end{matrix}$ where [.] denotes the fractional integral function and I is the set of integers. Then find $g (x) max . [x^{2}, f (x), | x |}, - 2 \leq x \leq 2 .$ View Solution
Question 69
Find the area of the region bounded by the curves $y = x^{2} and y = {sec}^{- 1} [- {sin}^{2} x],$ where [.] denotes G.I.F.View Solution
Question 70
Draw a graph of the function $f (x) = {cos}^{- 1} (4 x^{3} - 3 x), x \in [- 1, 1]$ and find the ara enclosed between the graph of the function and the x-axis varies from 0 to 1.View Solution
Question 71
Let $f (x)$ be continuous function given by $f (x) = {2 x, | x | \leq 1$ and $x^{2} + a x + b, | x | > 1} .$
Find the area of the region in the third quadrant bounded by the curves $x = - 2 y^{2} a n d y = f (x)$ lying on the left of the line $8 x + 1 = 0 .$ View Solution
Question 72
Let $[x]$ denotes the greatest integer function. Draw a rough sketch of the portions of the curves $x^{2} = 4 [\sqrt{x}] y and y^{2} = 4 [\sqrt{y}] x$ that lie within the square ${(x, y) ∣ 1 \leq x \leq 4, 1 \leq y \leq 4}$ . Find the area of the part of the square that is enclosed by the two curves and the line $x + y = 3$ .View Solution
Question 73
Find all the values of the parameter $a (a \leq 1)$ for which the area of the figure bounded by pair of straight lines $y^{2} - 3 y + 2 = 0$ and curves $y = [a] x^{2}, y = \frac{1}{2} [a] x^{2}$ is greatest , where [.] denotes the greatest integer function.View Solution
Question 74
Find the area in the 1* quadrant bounded by $[x] + [y] = n$ , where $n \in N and y = k$ (where $k \in n \forall k \leq n + 1$ ), where [.] denotes the greatest integer less than or equal to x.View Solution

All Exercises from ARIHANT MATHS (ENGLISH) Class 12 MATHS AREA OF BOUNDED REGIONS

EXERCISE FOR SESSION 1
EXERCISE FOR SESSION 2
EXERCISE (SINGLE OPTION CORRECT TYPE QUESTIONS)
EXERCISE (MORE THAN ONE CORRECT OPTION TYPE QUESTIONS)
EXERCISE (STATEMENT I AND II TYPE QUESTIONS)
EXERCISE (PASSAGE BASED QUESTIONS)
AREA OF BOUNDED REGIONS EXERCISE 5: MATCHING TYPE QUESTIONS
EXERCISE (SINGLE INTEGER ANSWER TYPE QUESTIONS)
AREA OF BOUNDED REGIONS EXERCISE 7: SUBJECTIVE TYPE QUESTIONS
EXERCISE (SUBJECTIVE TYPE QUESTIONS)
EXERCISE (QUESTIONS ASKED IN PREVIOUS 13 YEARS EXAM)
EXAMPLES

Home
Ask Doubt
Profile