Solved Examples from KC SINHA ENGLISH APPLICATIONS OF INTEGRALS - FOR COMPETITION for Class 12

Class 12	MATHS
Chapter	APPLICATIONS OF INTEGRALS - FOR COMPETITION
KC SINHA ENGLISH	Solved Examples
Medium	English
Academic Year	2023-2024

Question 1
Find the area of the region bounded by the x-axis and the curves defined by $y = tan x (w h e r e - \frac{π}{2} \leq x \leq \frac{π}{3})$ and $y = cot x (w h e r e \frac{π}{6} \leq x \leq \frac{3 x}{2})$ .View Solution
Question 2
Find the area bounded by the curves $x^{2} + y^{2} = 4, x^{2} = \sqrt{2} y, a n d x = y .$ View Solution
Question 3
Find the area bounded by the curves $x^{2} + y^{2} = 25, 4 y = ∣ ∣ 4 - x^{2} ∣ ∣,$ and $x = 0$ above the x-axis.View Solution
Question 4
Find the area of the region bounded by the curve C : y=tan x ,tangent drawn to C at x=pi/4, and the x-axis.View Solution
Question 5
The area bounded by the curve $y = x {(x - 1)}^{2},$ the y-axis and the line $y = 2$ is View Solution
Question 6
The area between the curve $y = 2 x^{4} - x^{2},$ the axis, and the ordinates of the two minima of the curve is 11/60 sq. units (b) 7/120 sq. units 1/30 sq. units (d) 7/90 sq. units View Solution
Question 7
Compute the area of the region bounded by the curves $y = e x {log}_{e} x and y = \frac{log x}{e x} .$ View Solution
Question 8
The line $y = m x$ bisects the area enclosed by the curve $y = 1 + 4 x - x^{2}$ and the lines $x = 0, x = \frac{3}{2} and y = 0 .$ Then the value of $m$ is View Solution
Question 9
Let $f (x) = M a ξ μ m {x^{2}, {(1 - x)}^{2}, 2 x (1 - x)},$ where $0 \leq x \leq 1 .$ Determine the area of the region bounded by the curves $y = f (x), x - a ξ s, x = 0,$ and $x = 1 .$ View Solution
Question 10
A curve $y = f (x)$ passes through the origin. Through any point $(x, y)$ on the curve, lines are drawn parallel to the coordinate axes. If the curve divides the area formed by these lines and coordinates axes in the ratio $m : n$ , find the curve.View Solution
Question 11
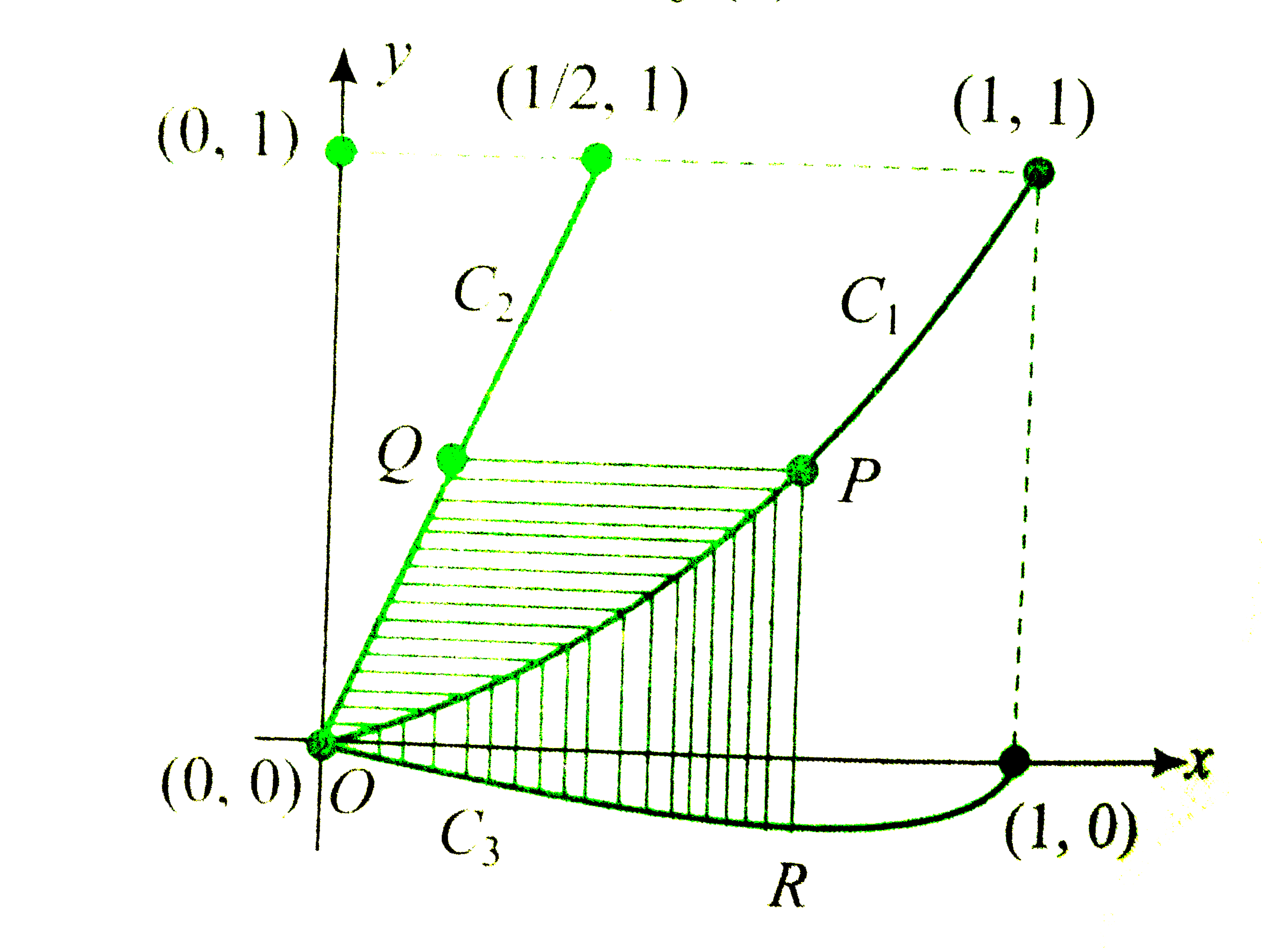
Let $C_{1} and C_{2}$ be the graphs of the functions $y = x^{2} and y = 2 x,$ respectively, where $0 \leq x \leq 1 . Let C_{3}$ be the graph of a function y=f(x), where $0 \leq x \leq 1, f (0) = 0 .$ For a point P on $C_{1},$ let the lines through P, parallel to the axes, meet $C_{2} and C_{3}$ at Q and R, respectively (see figure). If for every position of $P (o n C_{1}),$ the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View Solution
Question 12
Find the ratio of the areas in which the curve $y = [\frac{x^{3}}{100} + \frac{x}{35}]$ divides the circle $x^{2} + Y^{2} - 4 x + 2 y + 1 = 0$ . (where, [.] denotes the greated integer function).View Solution
Question 13
Find the area enclosed by circle $x^{2} + y^{2} = 4$ , parabola $y = x^{2} + x + 1$ , the curve $y = [\frac{{sin}^{2} x}{4} + \frac{cos x}{4}]$ and X-axis (where,[.] is the greatest integer function.View Solution
Question 14
Find the area of the region formed by $x^{2} + y^{2} - 6 x - 4 y + 12 \leq 0, y \leq x$ and $2 x \leq 5$ .View Solution
Question 15
Find all the possible values of $b > 0,$ so that the area of the bounded region enclosed between the parabolas $y = x - b x^{2} a n d y = \frac{x^{2}}{b}$ is maximum.View Solution
Question 16
Consider a square with vertices at $(1, 1), (- 1, 1), (- 1, - 1) and (1, - 1)$ . Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area. View Solution
Question 17
Let $A_{n}$ be the area bounded by the curve $y = {(tan x)}^{n}$ and the lines $x = 0, y = 0,$ and $x = \frac{π}{4} .$ Prove that for $n > 2, A_{n} + A_{n - 2} = \frac{1}{n - 1}$ and deduce $\frac{1}{2 n + 2} < A_{n} < \frac{1}{2 n - 2}$ View Solution
Question 18
Find the area of the region bounded by the curves $y = f (x), y = | g (x) |$ and lines $x = 0, x = 2$ , where $f$ and $g$ are continuous functions satisfying $f (x + y) = f (x) + f (y) - 8 x y$ for all $x, y \in R$ and $g (x + y) = g (x) + g (y) + 3 x y (x + y)$ for all $x, y \in R$ . Also $f' (0) = 8$ and g\'(0)=-4.View Solution
Question 19
Let $f (x)$ be continuous function given by $f (x) = {2 x, | x | \leq 1$ and $x^{2} + a x + b, | x | > 1} .$
Find the area of the region in the third quadrant bounded by the curves $x = - 2 y^{2} a n d y = f (x)$ lying on the left of the line $8 x + 1 = 0 .$ View Solution
Question 20
Sketch the region included between the curves $x^{2} + y^{2} = a^{2}$ and $\sqrt{| x |} + \sqrt{| y |} = \sqrt{a} (a .0)$ and find its area.View Solution
Question 21
The area of the region bounded by the parabola ${(y - 2)}^{2} = x - 1$ , the tangent to the parabola at the point (2,3) and the X-axis is View Solution
Question 22
Find the area of the region given by $x + y \leq 6, x^{2} + y^{2} \leq 6 y$ and $y^{2} \leq 8 x$ .View Solution
Question 23
Let $b \neq 0$ and for $j = 0, 1, 2, ... ., n$ . Let $S_{j}$ be the area of the region bounded by Y_axis and the curve $x \cdot e^{a y} = sin b y, \frac{j π}{b} \leq y \leq \frac{(j + 1) π}{b}$ . Show that $S_{0}, S_{1}, S_{2}, ... S_{n}$ are in geometric progression. Also, find their sum for a=-1 and $b = π$ .View Solution
Question 24
Find the area bounded by the curve $x^{2} = y, x^{2} = - y a n {d y}^{2} = 4 x - 3$ View Solution
Question 25
If [4a2 4a 1 4b2 4b 1 4c2 4c 1] [f-1 f1 f2] = [3a2 + 3a 3b2 + 3b 3c2 + 3c] fx is a quadratic function and its maximum value occurs at a point V. A is a point of intersection of y = f x with x-axis and point .B is such that chord AB subtends a right angled at V. Find the area enclosed by fx and chord AB.View Solution
Question 26
Find the area of the region bounded by the curves $y = x^{2}, y = ∣ ∣ 2 - x^{2} ∣ ∣, and y = 2,$ which lies to the right of the line x=1.View Solution
Question 27
Find the area bounded by curves $- 4 y^{2} = x$ and $x = 1 + 5 y^{2}$ View Solution
Question 28
The area bounded by the parabolas $y = {(x + 1)}^{2}$ and $y = {(x - 1)}^{2} a n d y = {(x - 1)}^{2}$ and the line $y = \frac{1}{4}$ is 4 sq. units (b) 1/6 sq. units 4/3 sq. units (d) 1/3 sq. units View Solution
Question 29
The area of the region between the curves $y = \sqrt{\frac{1 + sin x}{cos x}}$ and $y = \sqrt{\frac{1 - sin x}{cos x}}$ and bounded by the lines $x = 0$ and $x = \frac{π}{4}$ is View Solution
Question 30
Consider the function $y = f (x)$ defined implicitly by the equation $y^{3} - 3 y + x = 0$ on the interval $(- \infty, - 2) \cup (2, \infty)$ . The area of the region bounded by the curve $y = f (x)$ , the x-axis and the lines, $x = a, x = b$ , where $- \infty < a < b < - 2$ is (A) $\int_{a}^{b} \frac{x}{3 ({(f (x))}^{2} - 1)} d x + b f (b) - a f (a)$ (B) $- \int_{a}^{b} \frac{x}{3 ({(f (x))}^{2} - 1)} d x + b f (b) - a f (a)$ (C) $\int_{a}^{b} \frac{x}{3 ({(f (x))}^{2} - 1)} d x + b f (b) + a f (a)$ (D) $- \int_{a}^{b} \frac{x}{3 ({(f (x))}^{2} - 1)} d x - b f (b) + a f (a)$ View Solution
Question 31
Consider the function $f (x) = {\begin{matrix} x - [x] - \frac{1}{2} & x \notin 0 & x \in I \end{matrix}$ where [.] denotes the fractional integral function and I is the set of integers. Then find $g (x) max . [x^{2}, f (x), | x |}, - 2 \leq x \leq 2 .$ View Solution
Question 32
Consider the function $f (x) = {\begin{matrix} x - [x] - \frac{1}{2} & x \notin 0 & x \in I \end{matrix}$ where [.] denotes the fractional integral function and I is the set of integers. Then find $g (x) max . [x^{2}, f (x), | x |}, - 2 \leq x \leq 2 .$ View Solution
Question 33
Consider the function $f (x) = {\begin{matrix} x - [x] - \frac{1}{2} & if x \notin I 0 & if x \notin I \end{matrix}$ where $[.]$ denotes the greatest integer function and $g (x) = max . {x^{2}, f (x), | x |}, - 2 \leq x \leq 2$ . Now answer the question:Area bounded by $y = g (x)$ when $- 2 \leq x \leq 2$ is (A) $\frac{175}{48}$ (B) $\frac{275}{48}$ (C) $\frac{175}{24}$ (D) $\frac{275}{24}$ View Solution

All Exercises from KC SINHA ENGLISH Class 12 MATHS APPLICATIONS OF INTEGRALS - FOR COMPETITION

Home
Ask Doubt
Profile