BANSAL PHYSICS (HINDI) ELECTROSTATICS की EXERCISE-4 (IIT JEE ADVANCED PREVIOUS YEAR.S QUESTIONS) कक्षा 12 के लिए

कक्षा 12	भौतिकी
Chapter	ELECTROSTATICS
BANSAL PHYSICS (HINDI)	EXERCISE-4 (IIT JEE ADVANCED PREVIOUS YEAR.S QUESTIONS)
माध्यम	हिंदी
शैक्षणिक वर्ष	2023-2024

Question 1
एक गोलीय सममित तंत्र (spherical symmetric system) का वैद्युत विभव $(ϕ_{r})$ जो मूल बिन्दु पर रखा है। चित्र में दर्शाया गया है।

$ϕ_{r} = \frac{q}{4 π \in_{0} r} (r \geq R_{0})$
$ϕ_{r} = \frac{q}{4 π \in_{0} R_{0}} (r \leq R_{0})$
निम्न में से कौनसा विकल्प सही होगा। हल देखें
Question 2
एक लम्बा और खोखला चालक बेलन एक दूसरे और खोखले चालक बेलन जिसकी त्रिज्या बड़ी है उसके अन्दर सम-अक्षीय रखी है । दोनो ही बेलन शुरू में विद्युतीय अनावेशित है। हल देखें
Question 3
एक उदासीन चालक गोले के बाहर एक धनात्मक बिन्दु आवेश रखा है। गोले की सतह पर कुल आवेश होगा। हल देखें
Question 4
एक ठोस गोला जिस पर एक समान आवेश वितरित है, से एक छोटा गोला चित्रानुसार हटाया गया है। हटाये गये स्थान पर विद्युत क्षेत्र होगा।
हल देखें
Question 5
एक समान परिमाण के धन तथा ऋण आवेश $(0, 0, \frac{a}{2})$ तथा $(0, 0, - \frac{a}{2})$ पर रखे है। एक दूसरे धनात्मक बिन्दु आवेश को (-a, 0, 0) से (0, a, 0) तक विस्थापित करने में विद्युत क्षेत्र द्वारा किया गया कार्य क्या होगा? हल देखें
Question 6
चित्रानुसार एक निकाय के बिन्दु A, B तथा C पर $\frac{q}{3}, \frac{q}{3}$ व $- \frac{2 q}{3}$ आवेश रखे है। बिन्दु O वृत्त का केन्द्र तथा R वृत की त्रिज्या है। तथा कोण $C A B = 60^{\circ}$
हल देखें
Question 7
R त्रिज्या के नाभिक में +Ze आवेश असमान रूप से वितरित है। नाभिक के केन्द्र से दूरी r तथा आवेश घनत्व $ρ (r)$ ( एकांक आयतन में आवेश) के मध्य ग्राफ चित्र में प्रदर्शित किया गया है। केवल त्रिज्यीय दिशा में है।

नाभिक के अंदर सामान्यतः विद्युत क्षेत्र r पर रेखीय रूप से निर्भर करता है यह प्रदर्शित करता है। हल देखें
Question 8
R त्रिज्या के नाभिक में +Ze आवेश असमान रूप से वितरित है। नाभिक के केन्द्र से दूरी r तथा आवेश घनत्व $ρ (r)$ ( एकांक आयतन में आवेश) के मध्य ग्राफ चित्र में प्रदर्शित किया गया है। केवल त्रिज्यीय दिशा में है।

नाभिक के अंदर सामान्यतः विद्युत क्षेत्र r पर रेखीय रूप से निर्भर करता है यह प्रदर्शित करता है। हल देखें
Question 9
R, 2R, 3R त्रिज्याओं के तीन संकेंद्री धात्विक गोलीय कोशों में । आवेश क्रमश: $Q_{1}, Q_{2}, Q_{3}$ है। यह पाया जाता है कि कोशों की बाहरी सतहों पर पृष्ठीय आवेश घनत्व बराबर है। तब, कोशों को दिए गए आवेशों का अनुपात $Q_{1} : Q_{2} : Q_{3}$ है:हल देखें
Question 10
आवेश + Q के कूलॉम-क्षेत्र के प्रभाव में, इसके चारों ओर एक आवेश क्यू दीर्घ वृत्तीय कक्षा में विचरण कर रहा है। तब, सही वक्तव्य/वक्तव्यों का पता लगाएँ।हल देखें
Question 11
R त्रिज्या के एक ठोस गोले में आवेश Q है, जिसे आवेश घनत्व $ρ = k r^{a}$ के साथ इसके आयतन में वितरित किया गया है, जहां k और a नियतांक हैं और r इसके केंद्र से दूरी है। यदि $r = \frac{R}{2}$ पर विद्युत क्षेत्र, r = R पर विद्युत क्षेत्र का $\frac{1}{8}$ गुना है, तो a का मान ज्ञात कीजिए।हल देखें
Question 12
समान रूप से आवेशित एक गोलीय कोश जिसकी त्रिज्या R तथा प्रति एकांक क्षेत्रफल पृष्ठीय आवेश घनत्व $σ$ है। यदि यह दो अर्द्धगोलीय कोश से बना है तो दोनों को एक दूसरे के नजदीक लाने में लगाया गया F बल समानुपाती होगा।
हल देखें
Question 13
माना एक विद्युत क्षेत्र $\to E = E_{0} ˆ x$ , जहाँ $E_{0}$ स्थिरांक है। इस वैद्युत-क्षेत्र के कारण चित्र में दर्शाये आच्छादित क्षेत्र से गुजरने वाला वैद्युत-फ्लक्स है।
हल देखें
Question 14
त्रिज्या $R_{A}$ के धातु गोलीय कोश (spherical metal shell)A और त्रिज्या $R_{B} (< R_{A})$ के ठोस धातु के गोले B को एक दूसरे से बहुत दूर रखा गया है। प्रत्येक पर '+Q' आवेश है। उनको एक पतले धातु-तार से जोड़ने के बाद जो कथन सही है उनका चुनाव करें।हल देखें
Question 15
बराबर संख्या में इलेक्ट्रॉन तथा धन आयन समूह, जिसका घनत्व बहुत हो, को उदासीन प्लाज्मा कहते है। कुछ ठोस जिनमें स्वतंत्र इलेक्ट्रॉनो के बीच स्थिर धन-आयन स्थित होते है, को भी उदासीन प्लाज्मा की तरह लिया जाता है। माना कि मुक्त इलेक्ट्रॉनों का संख्या घनत्व 'N' है और प्रत्येक इलेक्ट्रॉन का द्रव्यमान 'm' है । वैद्युत क्षेत्र लगाने पर ये इलेक्ट्रॉन स्थिर धन-आयन की तुलना में अपनी जगह से खिसक जाते है। अब यदि वैद्युत क्षेत्र शून्य हो जाये तो इलेक्ट्रॉन $ω_{p}$ कोणीय आवृति से धन-आयन के सापेक्ष दोलन करते है। $ω_{p}$ को प्लाज्मा आवृति कहते है। इन दोलनों को परिवर्ती विद्युत क्षेत्र जिसकी कोणीय आवृत्ति है, लगाकर जारी रखा जा सकता है। तब वैद्युत क्षेत्र से प्राप्त कुछ ऊर्जा अवशोषित होती है व कुछ ऊर्जा परावर्तित होती है जब $ω$ बढ़कर $ω_{p}$ हो जाती है। तब इलेक्ट्रॉन समूह के सन्नादी हो जाने से सब ऊर्जा परावर्तित हो जाती है। यह धातु से परावर्तन के अधिक होने का कारण है।
इलैक्ट्रॉन आवेश को 'e' तथा परावैद्युतांक को $ε_{0}$ लेकर विमीय-सूत्र के द्वारा $ω_{p}$ के लिये सही समीकरण ज्ञात करें।हल देखें
Question 16
बराबर संख्या में इलेक्ट्रॉन तथा धन आयन समूह, जिसका घनत्व बहुत हो, को उदासीन प्लाज्मा कहते है। कुछ ठोस जिनमें स्वतंत्र इलेक्ट्रॉनो के बीच स्थिर धन-आयन स्थित होते है, को भी उदासीन प्लाज्मा की तरह लिया जाता है। माना कि मुक्त इलेक्ट्रॉनों का संख्या घनत्व 'N' है और प्रत्येक इलेक्ट्रॉन का द्रव्यमान 'm' है । वैद्युत क्षेत्र लगाने पर ये इलेक्ट्रॉन स्थिर धन-आयन की तुलना में अपनी जगह से खिसक जाते है। अब यदि वैद्युत क्षेत्र शून्य हो जाये तो इलेक्ट्रॉन $ω_{p}$ कोणीय आवृति से धन-आयन के सापेक्ष दोलन करते है। $ω_{p}$ को प्लाज्मा आवृति कहते है। इन दोलनों को परिवर्ती विद्युत क्षेत्र जिसकी कोणीय आवृत्ति है, लगाकर जारी रखा जा सकता है। तब वैद्युत क्षेत्र से प्राप्त कुछ ऊर्जा अवशोषित होती है व कुछ ऊर्जा परावर्तित होती है जब $ω$ बढ़कर $ω_{p}$ हो जाती है। तब इलेक्ट्रॉन समूह के सन्नादी हो जाने से सब ऊर्जा परावर्तित हो जाती है। यह धातु से परावर्तन के अधिक होने का कारण है।
एक धातु, जिसमें इलेक्ट्रॉनों का संख्या घनत्व $N \approx 4 \times 10^{27} m^{- 3}$ है, के लिये प्लाज्मा परावर्तन तरंगदैर्ध्य का मान ज्ञात करें। मानिये $ε_{0} \approx 10^{- 11}$ और $m \approx 10^{- 30}$ जहाँ यह मात्रायें अपने सही SI विमा में है।हल देखें
Question 17
निम्न में से कौन कथन सही है (हैं) ?हल देखें
Question 18
एक पतले गोलीय कोश (shell) का केंद्र मूल बिन्दु पर है व त्रिज्या R है। उस पर धन आवेश इस प्रकार वितरित है कि पृष्ठ-घनत्व एकसमान है। विद्युत क्षेत्र के मान $∣ ∣ \to E (r) ∣ ∣$ और विद्युत-विभव V (r) का, केन्द्र से दूरी r के साथ बदलाव का सर्वोत्तम वर्णन किस ग्राफ में है?हल देखें
Question 19
दो बड़ी ऊर्ध्वाधर व समांतर धातु की प्लेटो के बीच 1 सेमी की दूरी है। वे X विभवांतर के D.C स्त्रोत से जुडी है। दोनों प्लेटो के बीच एक प्रोटॉन स्थिर अवस्था में छोड़ा जाता है। छोड़े जाने के तुरंत बाद प्रोटॉन ऊर्ध्वाधर से $45^{\circ}$ कोण बनता हुआ गति करता है। तब X का मान लगभग है:हल देखें
Question 20
अपरिमित लम्बाई और R त्रिज्या के एक ठोस बेलन पर एकसमान आयतन-आवेष-घनत्व $ρ$ है। इसमें R/2 त्रिज्या का एक खोखला गोलीय-कोष बेलन के अक्ष पर केन्द्रित है (चित्र देखिये)। अक्ष से 2R दूरी पर स्थित बिन्दु P पर वैद्युत क्षेत्र $\frac{23 ρ R}{16 k ε_{0}}$ से दिया जाता है। तब k का मान क्या है ?
हल देखें
Question 21
L भुजा व O केन्द्र वाले एक समबाहु षट्भुज के कोनों पर 6 बिन्दु-आवेश चित्र में दर्शाये अनुरूप रखे हैं। $K = \frac{1}{4 π ε_{0}} \frac{q}{L^{2}}$ को मान कर निर्धारित करें कि कौन प्रकथन सही है/हैं?
हल देखें
Question 22
R व 2R त्रिज्या वाले दो अचालक ठोस गोलों को जिन पर क्रमशः $ρ_{1}$ तथा $ρ_{2}$ एकसमान आयतन आवेश घनत्व है, एक दूसरे से स्पर्श करते हुए रखा गया है। दोनों गोलों के केंद्रों को जोड़ने वाली रेखा के अनुदिश छोटे गोले के केंद्र से 2R दूरी पर कुल विद्युत क्षेत्र शून्य है। तब अनुपात $\frac{ρ_{1}}{ρ_{2}}$ का मान हो सकता है:हल देखें
Question 23
एक बिन्दु आवेश Q, एक एकसमान रेखीय आवेश घनत्व (Linear charge density) $λ$ . वाले अनन्त लम्बाई के तार तथा एक एकसमान पृष्ठ आवेश घनत्व (uniform surface charge density) $σ$ वाले अनन्त समतल चादर के कारण r दूरी पर विद्युत क्षेत्र की तीव्रतायें क्रमशः $E_{1} (r), E_{2} (r)$ तथा $E_{3} (r)$ हैं। यदि एक दी गई दूरी $r_{0}$ पर $E_{1} (r_{0}) = E_{2} (r_{0}) = E_{3} (r_{0})$ तब हल देखें
Question 24
संलग्न चित्र में दर्शाए गए तीन परावैद्युत (dielectric) गोलों पर, जिनकी त्रिज्याएँ क्रमशः R/2, R तथा 2R हैं, आवेश Q, 2Q तथा 4Q क्रमशः समान रूप से वितरित हैं। यदि बिन्दु P, जो प्रत्येक गोले के केन्द से R दूरी पर है, पर गोले 1, 2 तथा 3 के कारण विद्युत क्षेत्र का परिमाण क्रमशः $E_{1}, E_{2}$ व $E_{3}$ है, तब :
हल देखें
Question 25
चार आवेश Q_(1),Q_(2),Q_(3)" तथा "Q_(4), जिनके मान समान हैं, x-अक्ष के अनुदिश क्रमश: x=- 2a, -a,+a तथा +2a पर रखे हैं। एक अन्य घनावेश q+y- अक्ष पर $b > 0$ दूरी पर रखा है। आवेशों के चिह्न (sign) विकल्प सूची । में दिए हैं आवेश पर लगने वाले बलों की दिशा सूची II में दी गई है। सूची I को सूची II से सुमेलित कीजिए तथा सूचियों के नीचे दिये गए कोड का प्रयोग करके सही विकल्प चुनिए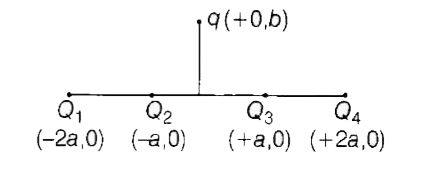
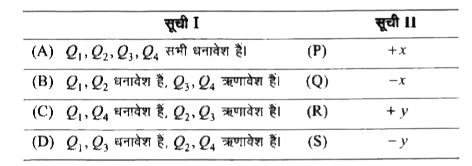हल देखें
Question 26
दिये गये चित्रों में दो स्थितियाँ दर्शायी गई है जिनमे दो अनंत लम्बाई के एकसमान रैखिक आवेश घनत्व $λ$ (धनात्मक) के सीधे तार परस्पर समांतर रखे गये है। चित्रानुसार q तथा $- q$ मान के दो बिंदु आवेश तारो से समान दूरी पर उनके वैद्युत क्षेत्र में साम्यावस्था में रखे हुये है। ये आवेश केवल X -दिशा में चल सकते है। यदि आवेशों को उनकी साम्यावस्था से थोड़ा-सा विस्थापित कराया जाये, तो सही विकल्प है:
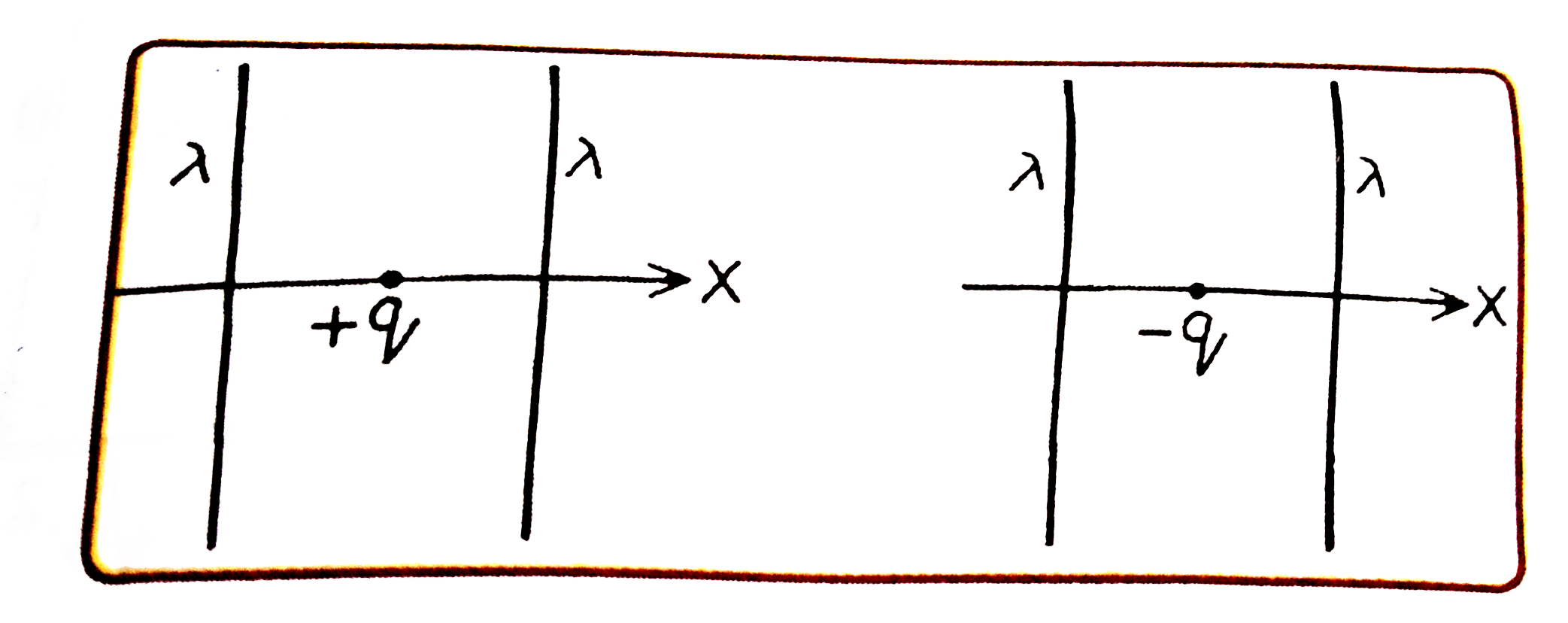हल देखें
Question 27
चित्रानुसार एक अनन्त लम्बाई के एकसमान आवेशित सीघे तार, जिसका रेखिक आवेश घनत्व $λ$ है, को y-z तल में Y-अक्ष के समान्तर $z = \frac{\sqrt{3}}{2}$ दूरी पर रखा गया है यदि इसके विद्युत क्षेत्र का, x-y तल में स्थित मूलबिन्दु पर केन्द्रिक ABCD आयताकार सतह से होकर जाने वाला फ्लक्स (epsi_(0)=" परविघुतांक का परिणाम") (lambdaL)/(n epsi_(0)) है तो का मान है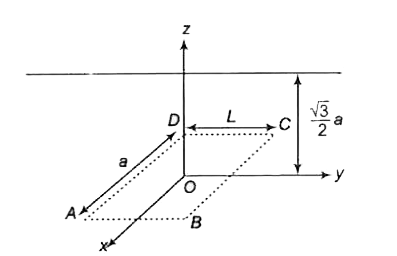 हल देखें
Question 28
धनात्मक बिन्दु आवेश +Q एक काल्पनिक अर्धगोलीय पृष्ठ जिसकी त्रिज्या R है, के बाहर रखा है। (जैसा कि चित्र में दिखाया गया है) निम्न में से कौनसा(से) प्रकथन सही है/हैं?
हल देखें

BANSAL PHYSICS (HINDI) ELECTROSTATICS की सभी प्रश्नावली कक्षा 12 के लिए

Home
Ask Doubt
Profile