JEE MAINS & ADVANCED PHYSICS (HINDI) अध्याय 20121:JEE ADVANCED पेपर - 2 (2012) की भाग -I : भौतिक विज्ञान खंड - III : बहुल सही उत्तर प्रकार कक्षा 12 के लिए
| कक्षा 12 | भौतिकी |
| Chapter | JEE ADVANCED पेपर - 2 (2012) |
| JEE MAINS & ADVANCED PHYSICS (HINDI) | भाग -I : भौतिक विज्ञान खंड - III : बहुल सही उत्तर प्रकार |
| माध्यम | हिंदी |
| शैक्षणिक वर्ष | 2023-2024 |
Question 2
एक रबर के गुब्बारे में दो मोल आदर्श हीलियम गैस 30∘ C पर है । गुब्बारा पूरी तरह फैल सकता है और उसके फैलने में कोई ऊर्जा खर्च नहीं होती, ऐसा मान लें । गुब्बारे में गैस का तापमान धीरे-धीरे 35∘ C कर दिया जाता है, तब उसका तापमान ... बढ़ाने में खर्च हुई ऊष्मा लगभग कितनी है ? (R = 8.31 J/mol.K लें)हल देखेंQuestion 3
एक डिस्क अपने केंद्र O पर एकसमान कोणीय चाल ω से घूम रही है । इसके व्यास के एक तरफ आच्छादित व दूसरी तरफ अन-आच्छादित क्षेत्र हैं (चित्र देखिये) । जब डिस्क चित्र में दर्शायी गई अवस्था में है तब दो कंकड़ P और ए एक ही समय पर y-2 तल में R की तरफ एक कोण पर प्रक्षेपित किये जाते हैं । दोनों का वेग डिस्क के सापेक्ष बराबर है । मानें कि (i) डिस्क के 18 चक्कर काटने से पहले ही कंकड़ डिस्क पर वापस आ गिरते हैं, (ii) उनका परास डिस्क की त्रिज्या के आधे से कम है, और (iii) ω वही बना रहता है । तब
हल देखेंQuestion 4
एक छात्र अनुनादी स्तम्भ का प्रयोग कर रहा है । स्तम्भ-नली का व्यास 4 cm और स्वरित्र-द्विभुज की आवृत्ति 512 Hz है । वायु का तापमान 38°C है और उसमें ध्वनि की चाल 336 m/s है । मीटर-स्केल का शून्य स्तम्भ-नली के ऊपरी सिरे के ठीक सामने है । प्रथम अनुनाद की अवस्था में स्तम्भ-नली में पानी के स्तर का पाठ्यांक है-हल देखेंQuestion 5
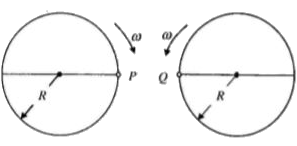
समान त्रिज्या R वाली दो एकसमान डिस्क अपनी धुरी पर एकसमान व स्थिर कोणीय चाल ω से विपरीत दिशा में घूम रही हैं । डिस्क एक ही क्षैतिज तल में हैं । समय t = 0 पर बिंदु P और Q चित्र में दर्शाये अनुसार आमने-सामने हैं । बिंदु P और बिंदु Q की आपेक्षिक चाल vr को एक आवर्तनकाल (T) में देखें । तब vr का समय के साथ परिवर्तन का किस ग्राफ में सर्वोत्तम वर्णन है ?
हल देखेंQuestion 9
1900 के आसपास हुई खोज के अनुसार β-क्षय प्रक्रम वास्तव में न्यूट्रॉन (n) का क्षय होता है । प्रयोगशाला में पाया गया है कि न्यूट्रॉन के क्षय होने पर एक प्रोटान (p) तथा एक इलेक्ट्रान (e−) जनित होते हैं । इसलिये, न्यूट्रॉन क्षय को द्वि-पिंडी क्षय-प्रक्रम मानकर, सैद्धांतिक गणना से यह सिद्ध किया गया कि इलेक्ट्रान की गतिज ऊर्जा का मान स्थिर रहना चाहिये । लेकिन प्रयोगों ने दिखाया कि इलेक्ट्रॉन की गतिज ऊर्जा के मान का संतत स्पेक्ट्रम होता है । त्रि-पिंडी क्षय प्रक्रम मानकर, अर्थात् n→p+e−+v−0, 1930 के आसपास Pauli ने इलेक्ट्रान का देखा गया ऊर्जा स्पेक्ट्रम समझाया । प्रति-न्यूट्रिनों (→ve) को द्रव्यमान-रहित व नगण्य ऊर्जा का मान कर और न्यूट्रान को स्थिर मान कर, संवेग व ऊर्जा संरक्षण के नियम गणना में लगाये गये जिससे इलेक्ट्रान की अधिकतम गतिज ऊर्जा को 0.8×106eV आंका गया । प्रोटान की गतिज ऊर्जा केवल प्रतिक्षेप ऊर्जा है ।
प्रति-न्यूट्रिनों की अधिकतम ऊर्जा हैहल देखेंQuestion 10
1900 के आसपास हुई खोज के अनुसार β-क्षय प्रक्रम वास्तव में न्यूट्रॉन (n) का क्षय होता है । प्रयोगशाला में पाया गया है कि न्यूट्रॉन के क्षय होने पर एक प्रोटान (p) तथा एक इलेक्ट्रान (e−) जनित होते हैं । इसलिये, न्यूट्रॉन क्षय को द्वि-पिंडी क्षय-प्रक्रम मानकर, सैद्धांतिक गणना से यह सिद्ध किया गया कि इलेक्ट्रान की गतिज ऊर्जा का मान स्थिर रहना चाहिये । लेकिन प्रयोगों ने दिखाया कि इलेक्ट्रॉन की गतिज ऊर्जा के मान का संतत स्पेक्ट्रम होता है । त्रि-पिंडी क्षय प्रक्रम मानकर, अर्थात् n→p+e−+v−0, 1930 के आसपास Pauli ने इलेक्ट्रान का देखा गया ऊर्जा स्पेक्ट्रम समझाया । प्रति-न्यूट्रिनों (→ve) को द्रव्यमान-रहित व नगण्य ऊर्जा का मान कर और न्यूट्रान को स्थिर मान कर, संवेग व ऊर्जा संरक्षण के नियम गणना में लगाये गये जिससे इलेक्ट्रान की अधिकतम गतिज ऊर्जा को 0.8×106eV आंका गया । प्रोटान की गतिज ऊर्जा केवल प्रतिक्षेप ऊर्जा है ।
यदि प्रति-न्यूट्रिनों का द्रव्यमान शून्य न होकर,3eV/c2 हो (जहाँ, c प्रकाश की गति है), तब इलेक्ट्रॉन की गतिज ऊर्जा, K, का परास होगा -हल देखेंQuestion 11
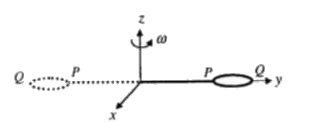
व्यापक रूप में किसी दृढ़ पिंड की गति को हम दो अलग-अलग गतियों के संयुक्त रूप में देख सकते हैं : (i) उसके संहति-केंद्र की किसी अक्ष के परितः गति, और (ii) उसके संहति-केन्द्र से गुजरनेवाले किसी तात्क्षणिक-अक्ष के परितः उसकी गति । यह आवश्यक नहीं है कि दोनों अक्ष स्थिर हों । उदाहरण के लिए हम क्षैतिज तल में रखी एकसमान डिस्क को लेते हैं जो अपनी परिधि पर एक द्रव्यमान-रहित छड़ से दृढ़ता से जुड़ी है (चित्र देखिये) । यह डिस्क-छड़ निकाय उद्गम के परितः ω कोणीय चाल से घर्षण-रहित क्षैतिज तल पर घूम रहा है । तब किसी भी क्षण डिस्क की गति को दो भिन्न गतियों के अध्यारोपण के रूप में देख सकते हैं। (i) डिस्क के संहति-केंद्र का z-अक्ष के सापेक्ष घूर्णन, और (ii) डिस्क का अपने संहति-केंद्र से गुजर रहे ऊर्ध्वाधर तात्क्षणिक-अक्ष पर घूर्णन (जो कि बिंदुओं P और ए के आपस में स्थान बदलने के रूप में दिखता है)। इस उदाहरण में इन दोनों घूर्णनों की कोणीय चाल ω
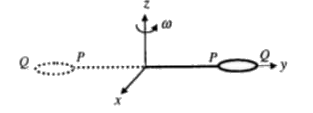
अब चित्र में दर्शाये गये उसी प्रकार के निकाय के दो भिन्न स्वरूपों (cases) पर ध्यान दें । Case (a) : डिस्क का पृष्ठ ऊर्ध्वाधर है और x-z तल के समांतर है, Case (b): डिस्क का पृष्ठ x-z तल से 45∘ कोण बनाता है एवं उसका क्षैतिज व्यास x-अक्ष के समांतर है । दोनों cases में डिस्क बिंदु P पर जड़ित है तथा यह निकाय z-अक्ष के परित: ω कोणीय चाल से घूर्णन करते हैं।
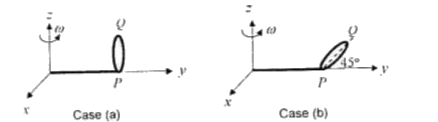
तात्क्षणिक-अक्ष (जो संहति-केंद्र से गुजर रहा है) के बारे में कौन सा प्रकथन सही है ?हल देखेंQuestion 12
व्यापक रूप में किसी दृढ़ पिंड की गति को हम दो अलग-अलग गतियों के संयुक्त रूप में देख सकते हैं : (i) उसके संहति-केंद्र की किसी अक्ष के परितः गति, और (ii) उसके संहति-केन्द्र से गुजरनेवाले किसी तात्क्षणिक-अक्ष के परितः उसकी गति । यह आवश्यक नहीं है कि दोनों अक्ष स्थिर हों । उदाहरण के लिए हम क्षैतिज तल में रखी एकसमान डिस्क को लेते हैं जो अपनी परिधि पर एक द्रव्यमान-रहित छड़ से दृढ़ता से जुड़ी है (चित्र देखिये) । यह डिस्क-छड़ निकाय उद्गम के परितः ω कोणीय चाल से घर्षण-रहित क्षैतिज तल पर घूम रहा है । तब किसी भी क्षण डिस्क की गति को दो भिन्न गतियों के अध्यारोपण के रूप में देख सकते हैं। (i) डिस्क के संहति-केंद्र का z-अक्ष के सापेक्ष घूर्णन, और (ii) डिस्क का अपने संहति-केंद्र से गुजर रहे ऊर्ध्वाधर तात्क्षणिक-अक्ष पर घूर्णन (जो कि बिंदुओं P और ए के आपस में स्थान बदलने के रूप में दिखता है)। इस उदाहरण में इन दोनों घूर्णनों की कोणीय चाल ω
अब चित्र में दर्शाये गये उसी प्रकार के निकाय के दो भिन्न स्वरूपों (cases) पर ध्यान दें । Case (a) : डिस्क का पृष्ठ ऊर्ध्वाधर है और x-z तल के समांतर है, Case (b): डिस्क का पृष्ठ x-z तल से 45∘ कोण बनाता है एवं उसका क्षैतिज व्यास x-अक्ष के समांतर है । दोनों cases में डिस्क बिंदु P पर जड़ित है तथा यह निकाय z-अक्ष के परित: ω कोणीय चाल से घूर्णन करते हैं।
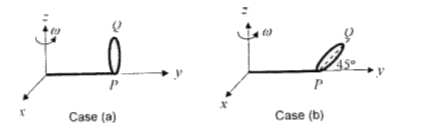
तात्क्षणिक-अक्ष (जो संहति-केंद्र से गुजर रहा है) के परितः घूर्णन की कोणीय चाल के बारे में कौन सा प्रकथन सही है ?हल देखेंQuestion 13
अधिकतर पदार्थों का अपवर्तनांक, n>1 होता है । इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम sinθ1sinθ2=n2n1 के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है । लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती । विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक n=(cv)=±√εrμr होता है, जहाँ c विद्युत-चुम्बकीय तरंगों की निर्वात में चाल तथा v उनकी माध्यम में चाल हैं, εr व μr क्रमश: माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं । आम पदार्थों में εr , व μr , दोनों धनात्मक होते हैं, अर्थात् माध्यम का n धनात्मक है । जब εr व μr दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा । ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-material) कहते हैं । वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते । चूँकि । ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है । तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती ।
सही प्रकथन चुनें ।हल देखेंQuestion 14
अधिकतर पदार्थों का अपवर्तनांक, n>1 होता है । इसलिये जब कोई प्रकाश किरण वायु से किसी प्राकृतिक पदार्थ में प्रवेश करती है तब, Snell's नियम sinθ1sinθ2=n2n1 के अनुसार, अपवर्तित किरण अभिलंब की तरफ झुकती है । लेकिन यह कभी भी अभिलंब के आपतित किरण वाले ओर से बाहर नहीं निकलती । विद्युत-चुम्बकत्व के अनुसार, किसी माध्यम का अपवर्तनांक n=(cv)=±√εrμr होता है, जहाँ c विद्युत-चुम्बकीय तरंगों की निर्वात में चाल तथा v उनकी माध्यम में चाल हैं, εr व μr क्रमश: माध्यम की सापेक्ष विद्युतशीलता व चुंबकशीलता हैं । आम पदार्थों में εr , व μr , दोनों धनात्मक होते हैं, अर्थात् माध्यम का n धनात्मक है । जब εr व μr दोनों ऋणात्मक हों तब हमें n का ऋणात्मक वर्गमूल लेना होगा । ऐसे ऋणात्मक n वाले पदार्थ अब अप्राकृतिक रूप में तैयार किये जा सकते हैं, और उन्हें मैटा-पदार्थ (meta-material) कहते हैं । वे बिलकुल अलग तरह का प्रकाशिक गुणधर्म दर्शाते हैं, परंतु भौतिक नियमों का उल्लंघन नहीं करते । चूँकि । ऋणात्मक है, अपवर्तित प्रकाश की चलने की दिशा में परिवर्तन होता है । तथापि आम पदार्थों की तरह इन मैटा-पदार्थों में भी अपवर्तन पर प्रकाश की आवृत्ति नहीं बदलती ।
वायु (air) से मैटा-पदार्थ पर आपतित प्रकाश-किरण के लिये उपयुक्त किरण-चित्र हैहल देखेंQuestion 17
चित्र में दिखाये निकाय के हिस्से हैं : (i) 3R बाहरी-त्रिज्या की रिंग, जो क्षैतिज सतह पर ω कोणीय चाल से दक्षिणावर्त । बिना फिसले लुढ़क रही है, और (ii) 2R त्रिज्या की भीतरी डिस्क जो ω/2 कोणीय चाल से वामावर्त घूम रही है । घर्षणरहित बॉल-बियरिंग (गोलियाँ) रिंग और डिस्क को एक दूसरे से अलग रखते हैं । निकाय x - z. तल में है । भीतरी डिस्क पर बिंदु P उद्गम से R दूरी पर है और OP क्षैतिज से 30° का कोण बनाता है । तब क्षैतिज सतह के सापेक्ष-
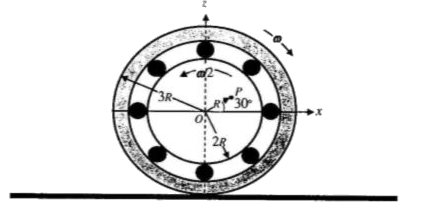हल देखें
