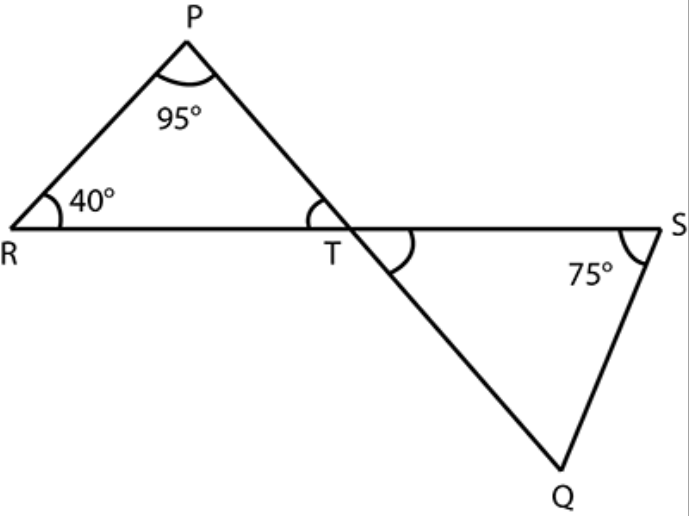
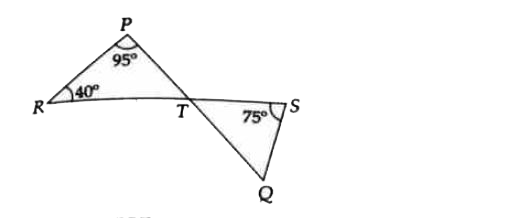
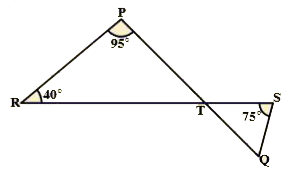
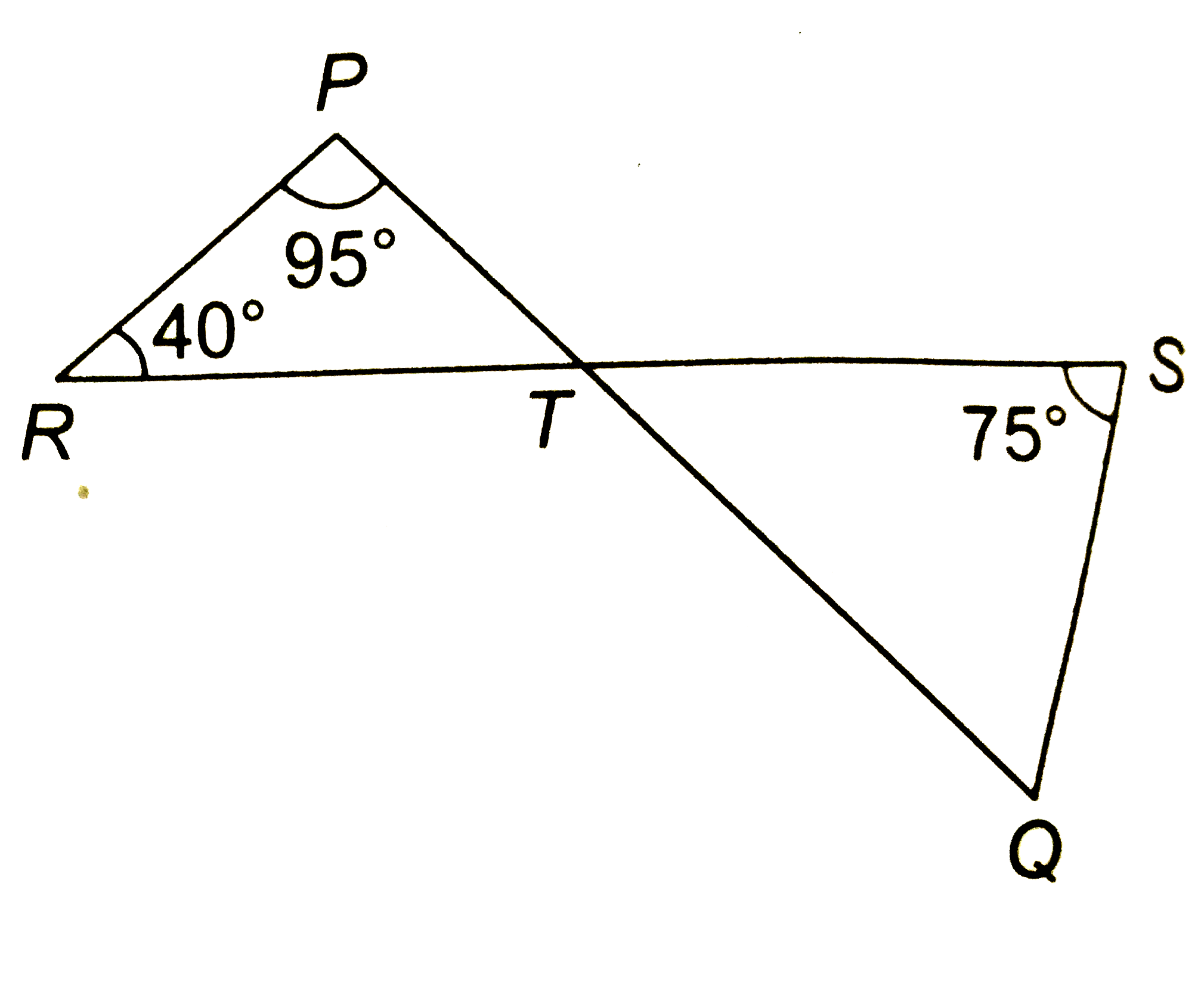
In the figure if lines PQ and RS intersect at point T such that ∠ PRT = 40° ∠ RPT = 95° and ∠TSQ = 75° find ∠SQT.
In the given figure lines PQ and RS intersect at point T such that ∠PRT = 40° ∠RPT = 95° and ∠TSQ = 75°. In ∆PRT ∠PRT + ∠RPT + ∠PTR = 180° [Angle sum property of a triangle] ⇒ 40° + 95° + ∠PTR = 180° ⇒ 135° + ∠PTR = 180° ⇒ ∠PTR = 180° – 135° = 45° Also ∠PTR = ∠STQ [Vertical opposite angles] ∴ ∠STQ = 45°Now in ∆STQ ∠STQ + ∠TSQ + ∠SQT = 180° [Angle sum property of a triangle] ⇒ 45° + 75° + ∠SQT = 180° ⇒ 120° + ∠SQT = 180° ⇒ ∠SQT = 180° – 120° = 60° Hence ∠SQT = 60° Ans.
Related Solutions
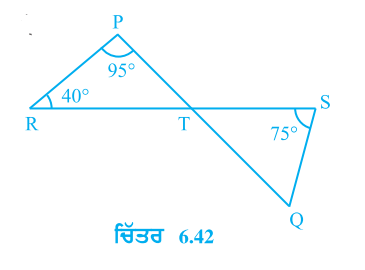
In Fig. 6.42, if lines PQ and RS intersect at point T, such that , find .
View Solutionਚਿੱਤਰ 6.42 ਵਿਚ, ਜੇ ਰੇਖਾਵਾਂ PQ ਅਤੇ RS ਬਿੰਦੂ T 'ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਕੱਟਦੀਆਂ ਹਨ ਕਿ ਅਤੇ ਹੈ, ਤਾਂ ਪਤਾ ਕਰੋ।
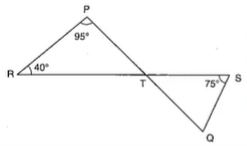
View Solutionआकृति में, यदि रेखाएँ PQ और RS बिंदु T पर इस प्रकार प्रितिच्छेद करती है । की और है, तो ज्ञात कीजिये ।

View SolutionIn figure, if lines and intersect at a point such that and find
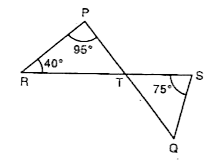
View SolutionIn figure, if lines PQ and RS intersect at point T, such that and. find .
View SolutionIn given figure, if lines PQ and RS intersect at point T, such that and , find
View SolutionIn the given figure lines PQ and RS intersect at point T such that and find
View Solutionಚಿತ್ರದಲ್ಲಿ PQ ಮತ್ತು RS ರೇಖೆಗಳು T ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತಿವೆ. = , = ಮತ್ತು = , ಆದರೆ ಕಂಡುಹಿಡಿಯಿರಿ.
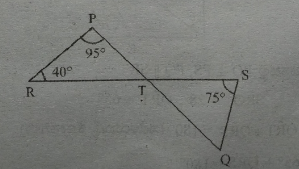
View SolutionIn Fig , if lines PQ and RS intersect at point T, such that
View SolutionIn the given Fig.
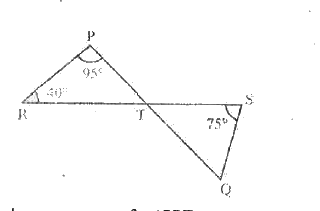
 , if lines PQ and RS intersect at point T, such that , and find .
, if lines PQ and RS intersect at point T, such that , and find .
View SolutionIn the given Fig.
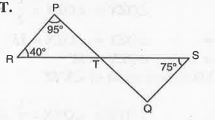
 , if lines PQ and RS intersect at point T, such that , and find .
, if lines PQ and RS intersect at point T, such that , and find .
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that , find .

View Solutionचित्र में, यदि रेखाएँ PQ और RS बिन्दु T पर इस प्रकार प्रतिच्छेद करती हैं की और , तो ज्ञात कीजिए |
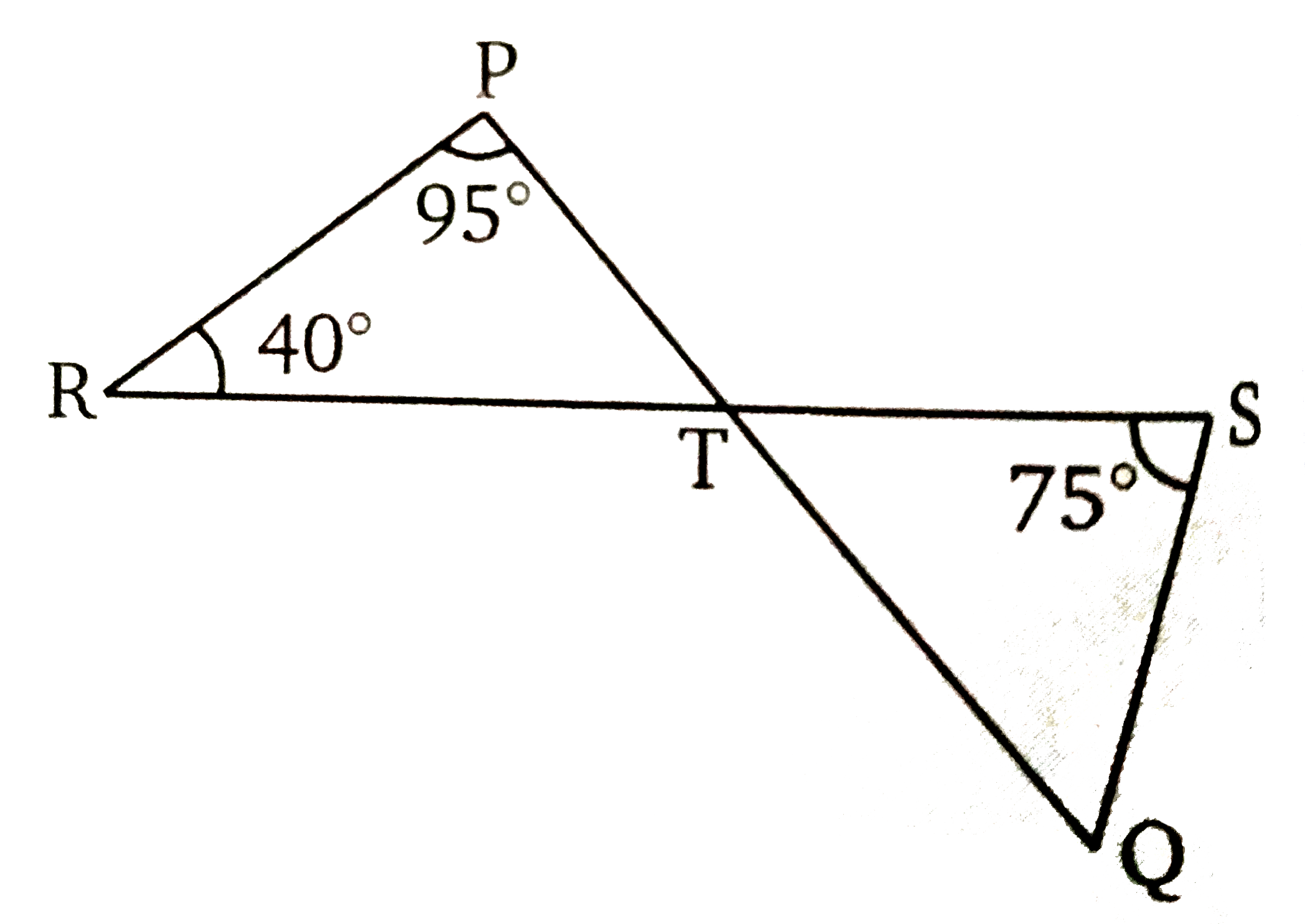
View Solutionआकृति में , यदि रेखाएँ PQ और RS बिंदु T पर इस प्रकार प्रतिच्छेद करती है कि और है , तो ज्ञात कीजिए ।

View SolutionIn the given figure if line segments PQ and RS intersect at point T, such that and , find
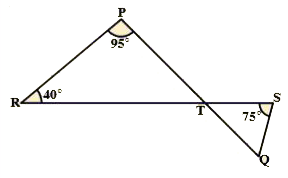
View SolutionIn the given figure if line segments PQ and RS intersect at point T, such that and , find
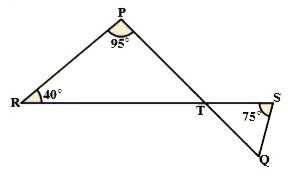
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that and find .

View SolutionIn the given figure if line segments PQ and RS intersect at point T, such that and , find
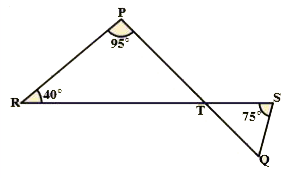
View SolutionIn the given figure if line segments PQ and RS intersect at point T, such that and , find
View Solutionआकृति में, यदि रेखाएं PQ और RS बिंदु T पर इस प्रकार प्रतिच्छेद करती है की और है, तो ज्ञात कीजिय |
View Solution