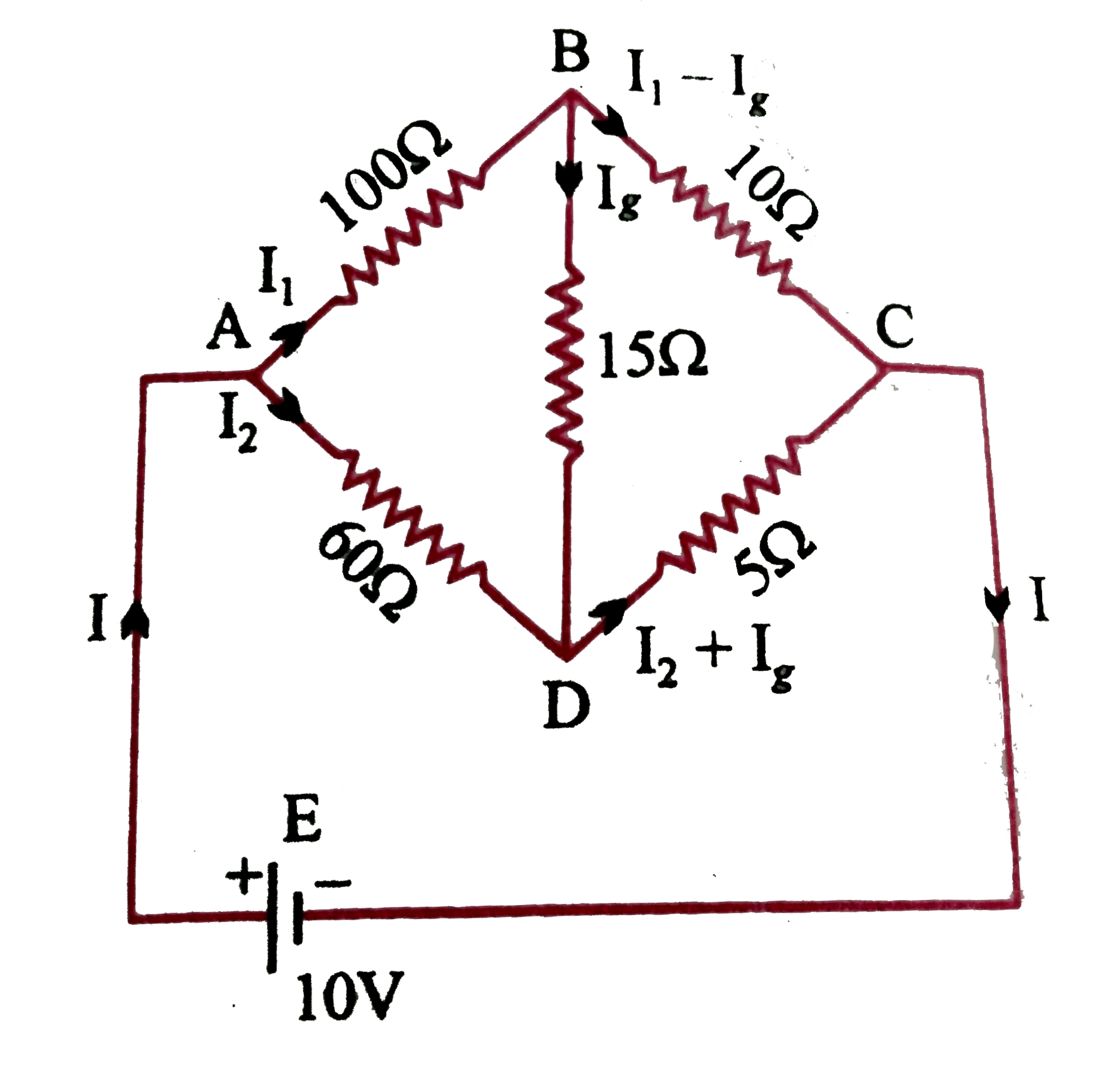
The four arms of a Wheatstone bridge have the following resistances : AB = 100 BC = 10 CD = 4 DA = 50 Ω. A galvanometer of 20 Ω resistance is connected across BD. Use Thevenin’s theorem to compute the current through the galvanometer when a p.d. of 10 V is maintained across AC.
i When galvanometer is removed from Fig. 2.139 a we get the circuit of Fig. 2.139 b. ii Let us next find the open-circuit voltage Voc also called Thevenin voltage Vth between points B and D. Remembering that ABC as well as ADC is a potential divider on which a voltage drop of 10 V takes place we get Potential of B w.r.t. C = 10 × 10/110 = 10/11 = 0.909 V Potential of D w.r.t. C = 10 × 4/54 = 20/27 = 0.741 V ∴ p.d. between B and D is Voc or Vth = 0.909 − 0.741 = 0.168 V iii Now remove the 10-V battery retaining its internal resistance which in this case happens to be zero. Hence it amounts to short-circuiting points A and C as shown in Fig. iv Next let us find the resistance of the whole network as viewed from points B and D. It may be easily found by noting that electrically speaking points A and C have become one as shown in Fig. . It is also seen that BA is in parallel with BC and AD is in parallel with CD. Hence RBD = 10 || 100 + 50 || 4 = 12.79 Ωv Now so far as points B and D are connected the network has a voltage source of 0.168 V and internal resistance Ri = 12.79 Ω. This Thevenin’s source is shown in Fig. vi Finally let us connect the galvanometer initially removed to this Thevenin source and calculate the current I flowing through it. As seen from Fig. I = 0.168/12.79 + 20 = 0.005 A = 5 mA
Related Solutions
The four arms of a Wheatstone bridge (Fig. 3.26) have the following resistances:
.

A galvanometer of 15W resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
View SolutionThe four arms of a Wheatstone bridge have the following resistance :
, and

A galvanometer of resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
View SolutionThe four arms of a Wheatstone bridge (Fig. 3.26) have the following resistances:
.

A galvanometer of 15W resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
View SolutionThe four arms of a Wheatstone bridge have resistances as shown in the figure. A galvanometer of 15 resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.

View SolutionThe four arms as a Wheatstone bridge have the following resistances:
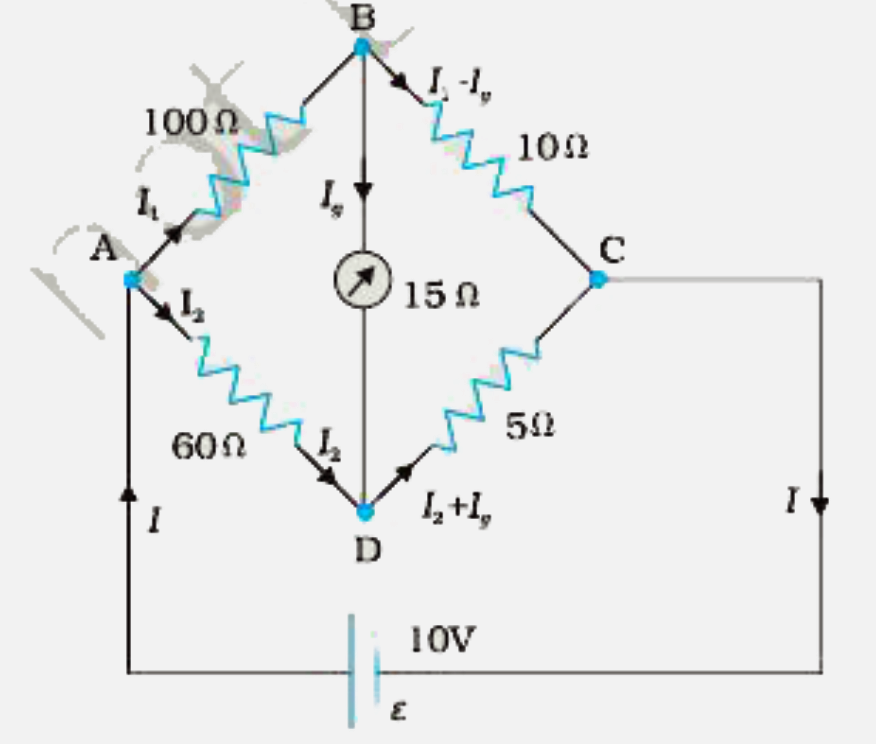
A galvanometer of resistacne is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
View SolutionThe four arms of a Wheatstone bridge (Fig. 3.26) have the following resistances:
.

A galvanometer of 15W resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
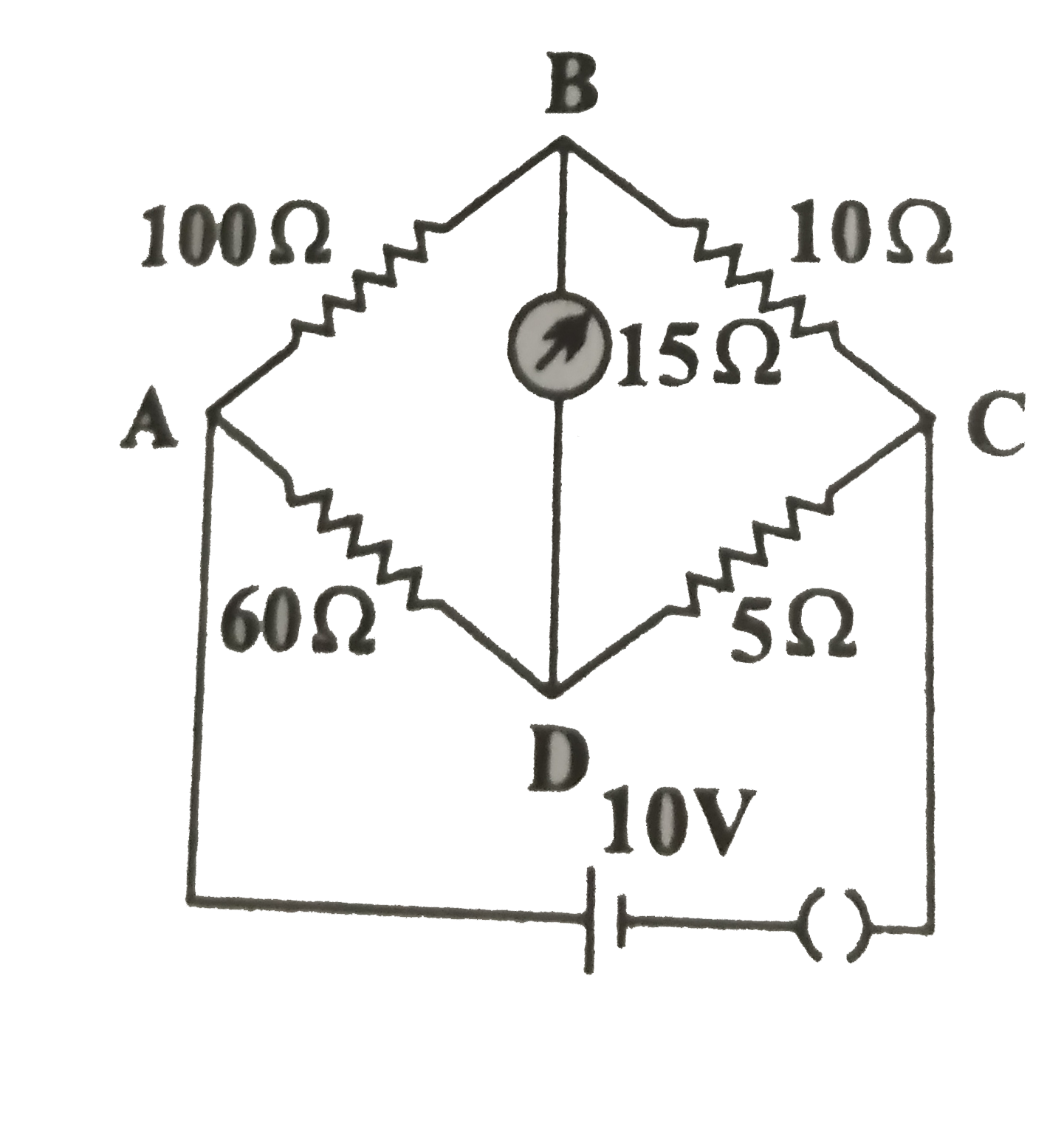
View SolutionThe four arms of a Wheatstone bridge (Fig.) have the following resistances : AB= 100Omega, BC= 10Omega, CD =5 Omega, and DA=60Omega A galvanometer of 15 0 resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 Vis maintained across AC.
View SolutionThe four arma os a Wheatstone bridge have the following resistances:
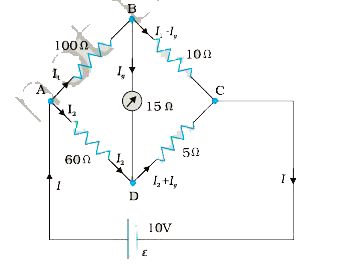
A galvanometer of resistacne is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
View SolutionThe four arms of a Wheastone bridge (Figure) have the following resistance : AB=100Omega, BC=10Omega, CD=5Omega and DA=60Omega A galvanometer of 15Omega resistance is connected across BD. Calculate the current through the galvano - meter when a potential difference of 10 V is maintained across AC,
View Solutionव्हीटस्टोन सेतु की चार भुजाओं (चित्र ) के प्रतिरोध निम्नवत हैं -
तथा |
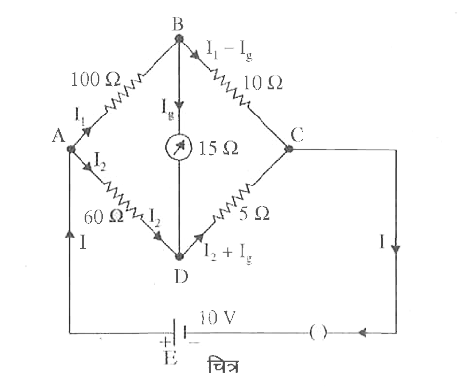
15 प्रतिरोध के एक गैल्वेनोमीटर को BD के बीच जोड़ा गया है। गैल्वेनोमीटर से प्रवाहित होने वाली धारा को परिकलित कीजिए। AC के मध्य 10V विभवान्तर है।
View SolutionThe following resistances of the four arms of a Wheatstone bridge are shown in the figure. AB = 100Omega, BC = 10Omega, CD = 5Omega And DA = 60Omega Huh. 15Omega A galvanometer of resistance is connected to the BD side, then the current flowing through the galvanometer creating a potential difference of 10 volts on the AC side will be.
View SolutionThe resistance of each arm of Wheatstone Bridge is 10 Omega . A resistance of 10 Omega is connected in series with the galvanometer then equivalent resistance across battery will be
View Solutionकिसी व्हीटस्टोन सेतु की चार भुजाओं के प्रतिरोध आरेख में दर्शाए अनुसार हैं। BD के सिरों पर प्रतिरोध का कोई गैल्वैनोमीटर संयोजित है। जब AC के सिरों पर 10V का विभवान्तर स्थापित किया जाता है तो गैल्वैनोमीटर से प्रवाहित धारा परिकलित कीजिए।
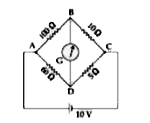
View Solutionव्हीटस्टोन सेतु कि चार भुजाओ के प्रतिरोध निम्न चित्रानुसार है जहाँ तथा प्रतिरोध के एक गैल्वेनोमीटर को के बीच जोड़ा गया है । गैल्वेनोमीटर से प्रवाहित होनी वाली धारा को परिकलित कीजिए । के मध्य विभवांतर है ।
View Solutionव्हीटस्टोन सेतु के चार भुजाओं के प्रतिरोध निम्नवत है- तथा प्रतिरोध के एक धारामापी को BD के बीच जोड़ा गया है। धारामापी में प्रवाहित होने वाली धारा को परिकलित कीजिए। AC के मध्य 10V विभवांतर है।
View SolutionIn a wheatstone bridge the four arms have each resistance of 50 ohm.The galvanometer current is "
View SolutionIn a wheatstone bridge, the resistance of the arms of the bridge are AB = , BC = ,AD = and DC = . The terminals of negligible resistance to A and C. If a galvanometer of resistance is connected between B and D, find the current in the galvanometer.
View Solutionव्हीटस्टोन सेतु की चार भुजाओ ( चित्र 3 .26 ) के प्रतिरोध निम्नवत है :
तथा
View Solutionएक व्हीटस्टोन ब्रिज की प्रत्येक भुजा का प्रतिरोध है। एक का प्रतिरोध , गैल्वेनोमीटर के साथ श्रेणीक्रम में जोड़ा जाता है। तब बैटरी के सिरों का ब्रिज का तुल्य प्रतिरोध होगा
View SolutionCalculate the value of the shunt resistance when connected across a galvanometer of resistance will allow 1/10 th of the current to pass through the galvanometer.
View Solution