सिद्ध कीजिये की समस्त त्रिभुजों के समुच्चय A में, R={T1,T2}:T1,T2 के समरूप है, द्वारा परिभाषित सम्बन्ध R एक तुल्यता सम्बन्ध है। भुजाओं 3, 4, 5 वाले समकोण त्रिभुज T3 पर विचार कीजिये। T1,T2 और T3 में से कौन से त्रिभुज परस्पर संबंधित हैं?
Text Solution
(i) प्रत्येक त्रिभुज अपने आपके समरूप होता हैं|
∴T,T के समरूप हैं प्रत्येक T∫A के लिए अर्थात TRT∀T∫A
अतः R, A पर सवतुल्य सम्बन्ध हैं|
(ii) T1RT2⇒T1,T2 के समरूप हैं|
⇒T2.T1 के समरूप हैं
⇒T2,RT1
∴ R,A पर सम्बंधित सम्बन्ध हैं|
(ii) T1T2 तथा T2T2⇒T1,T2 के समरूप हैं तथा T2,T3 के समरूप हैं| ⇒T1RT3
∴ R,A पर सम्बन्ध हैं|
अतः R,A पर एक तुल्यता सम्बन्ध हैं|
Second part: चूँकि त्रिभुज T1 तथा T2 की भुजाएँ समानुपाती नहीं हैं इसलिए T_(1) cancel(R) T_(2) लेकिन त्रिभुज T1 तथा T3 की भुजाएँ समानुपाती हैं, इसलिए T1RT3 साथ ही T2RT3
|
Topper's Solved these Questions
Knowledge Check
Shown below are the black body radiation curves at temperature T1 and T2(T2>T1). Which of the following plots is correct?
A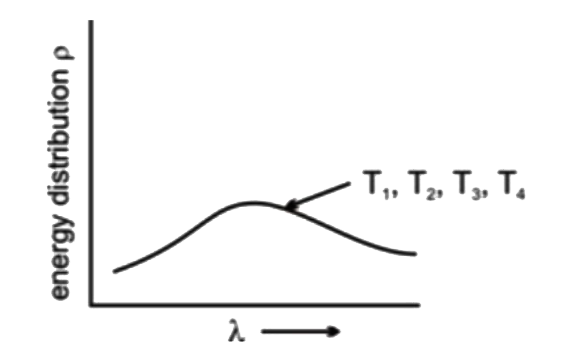 B
B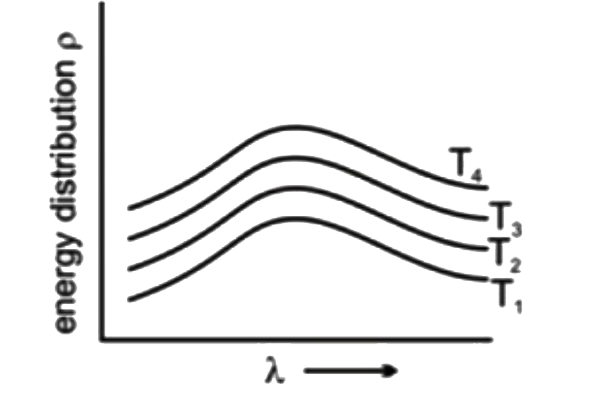 C
C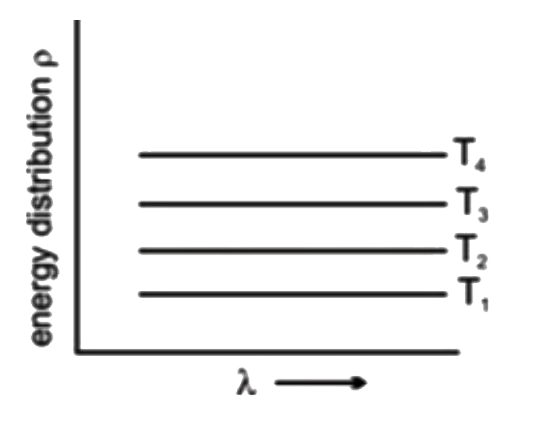 D
D