फलन तथा पर विचार करें जो इस प्रकार परिभाषित है, f(1) = a, f(2) = c, g(a) = apple, g(b) = ball तथा g(c) = cat. दिखाएँ कि f, g तथा gof व्युत्क्रमणीय है। तथा निकालें तथा दिखाएँ कि .
दिया है
तथा
माना कि A = {1,2,3), B = {a,b,c} , C = {apple, ball, cat}

दिया f(1) = a
f(2) = b
f(3) = c
तथा g(a) = apple
g(b) = ball
g(c) = cat
यहाँ इस प्रकार परिभाषित है,
gof(1) = g[f(1)] = g(a) = apple
gof(2) = g[f(2)] = g(b) = ball
gof(3) = g[f(3)] = g(c) = cat

स्पष्टतः f, g, gof एकैकी आच्छादक है और इसलिए तथा का अस्तित्व है।
अब इस प्रकार परिभाषित है,
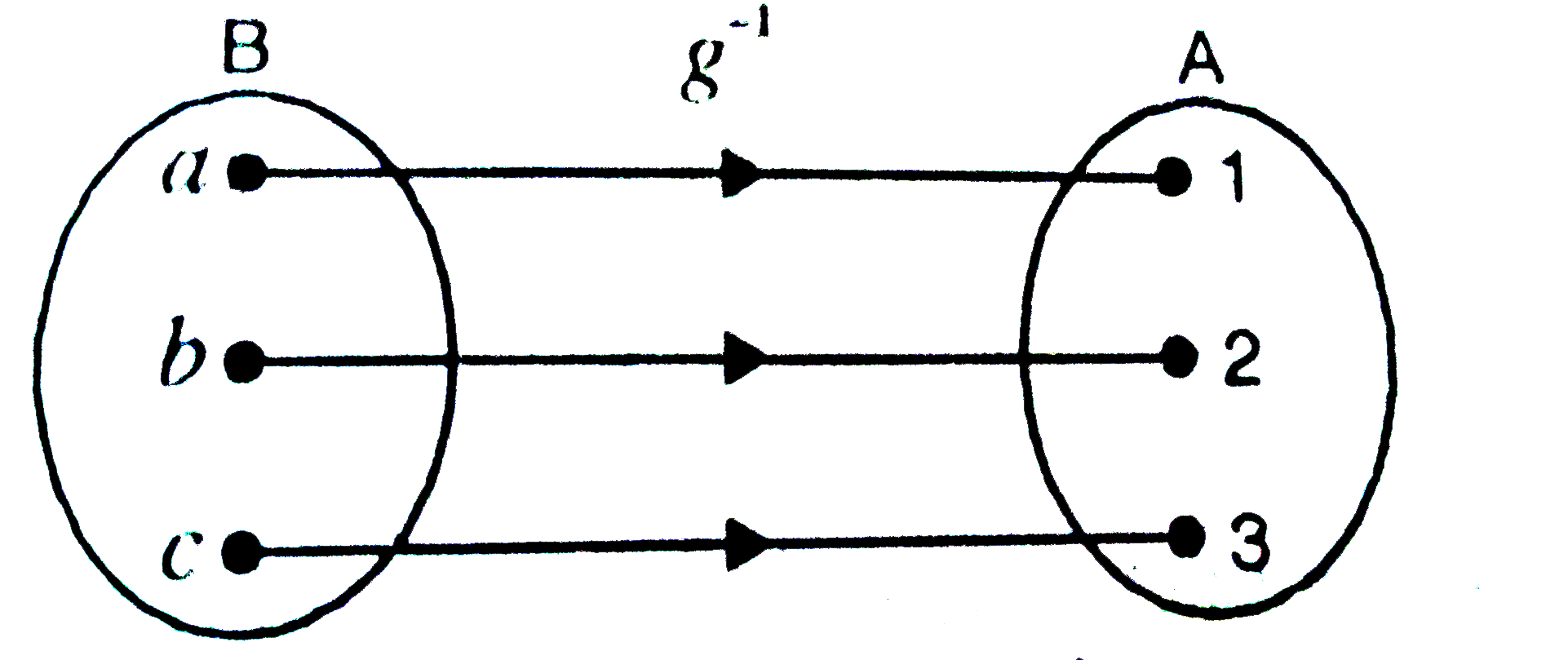
तथा इस प्रकार परिभाषित है,
(apple) (ball) = b and (cat) = c
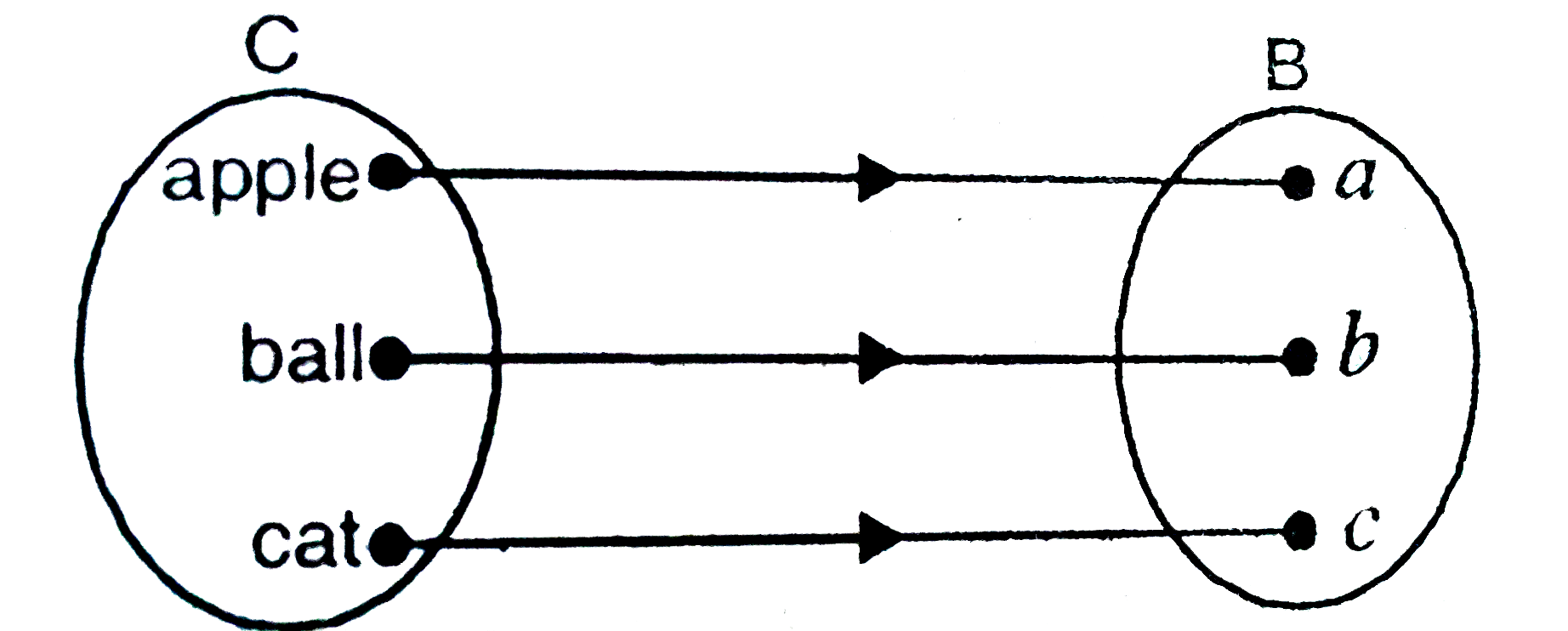
साथ ही इस प्रकार परिभाषित है,
(apple) =1, (ball) = 2, (cat) = 3
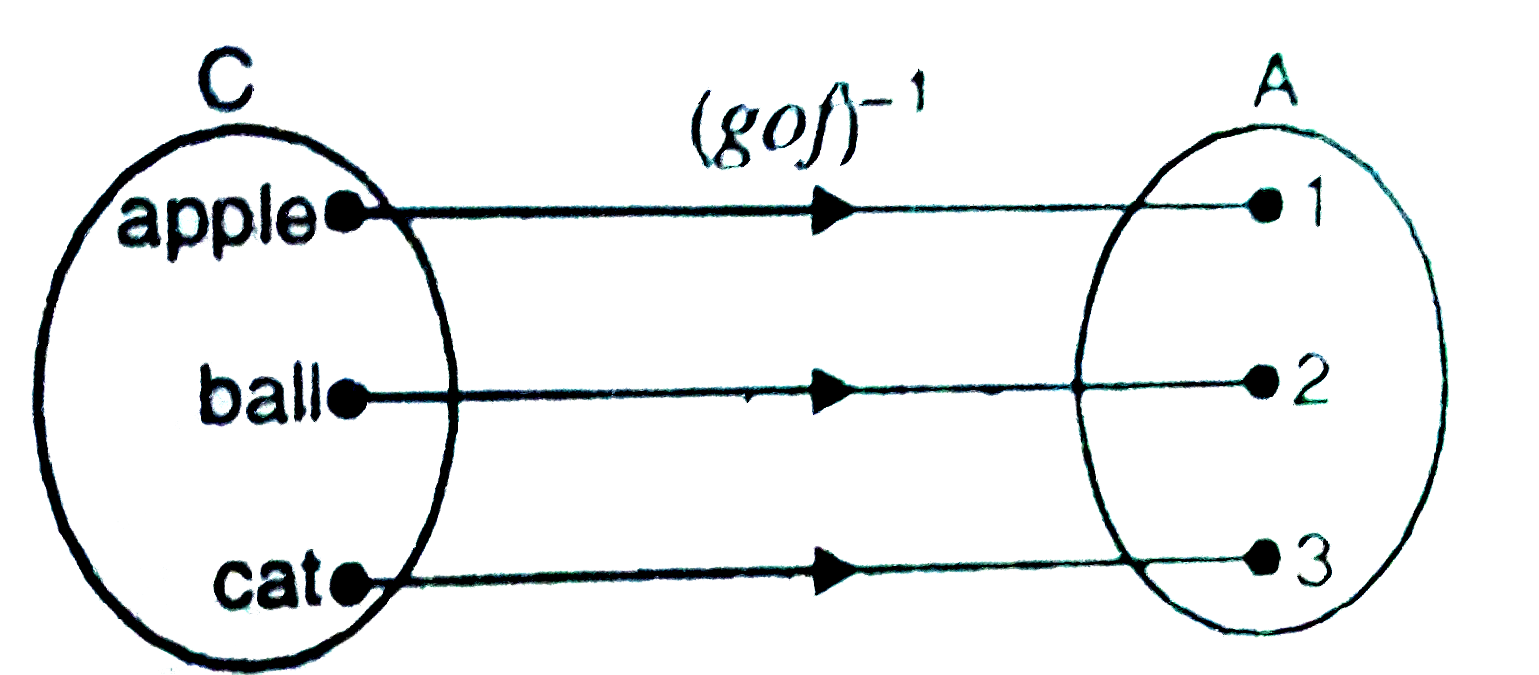
साबित करना है कि
अब (apple) =
तथा
इस प्रकार
स्पष्टतः

तथा का अस्तित्व है, दिखने का दूसरा तरीका :
इस प्रकार ताकि
अतः का अस्तित्व है अर्थात f व्युत्क्रमणीय है
ताकि
अतः का अस्तित्व है अर्थात g व्युत्क्रमणीय है तथा
अतः का अस्तित्व है अर्थात gof व्युत्क्रमणीय है।
Topper's Solved these Questions
- फलन BOOK - KC SINHACHAPTER - फलन EXERCISE - अभ्यास 2.1
29 Videos
- फलन BOOK - KC SINHACHAPTER - फलन EXERCISE - अभ्यास 2.2
12 Videos
- प्रायिकता का गुणन प्रमेय BOOK - KC SINHACHAPTER - प्रायिकता का गुणन प्रमेय EXERCISE - 32.2
24 Videos
- बरनौली परीक्षण और द्विपद बंटन BOOK - KC SINHACHAPTER - बरनौली परीक्षण और द्विपद बंटन EXERCISE - OBJECTIVE QUESTIONS
10 Videos
Similar Questions
माना कि A = {1, 2, 3}, B = {4, 5, 6, 7} तथा माना कि f = {(1, 4), (2, 5), (3, 6)} A से B में एक फलन है। दिखाएँ कि f एकैकी है।
View Solutionमाना कि f = {(1, 2), (3, 5), (4, 1)} तथा g = {(2, 3), (5, 1), (1, 3)} द्वारा प्रदत्त है। fog तथा gof ज्ञात करें।
View Solutionएक न्यायय सिक्का और एक अभिनत पाए को उछाला गया । मान ले A घटना 'सिक्के पर चित प्रकट होता है और B घटना 'पास पर संख्या 3 प्रकट होती है' को निरूपित करते है। परीक्षण कीजिए की घटनाएँ A और B स्वतंत्र है या नहीं ?
View SolutionIn a box containing 100 bulbs , 10 are defective. What is the probability that out of a sample of 5 bulbs, none is defective ?
View Solutionf : { 1,2,3} → {a, b , c} तथा g : {a , b ,c} → {सेब , गेंद , बिल्ली } f (1) = a , f(2) = b , f (3) = c , g (a) = सेब g (b) = गेंद और g(c) = बिल्ली व्दारा परिभाषित फलनों पर विचार कीजिए । सिद्ध कीजिए कि f , g , gof व्युत्क्रमणीय हैं । f−1,g−1तथा(gof)−1 ज्ञात कीजिए तथा दर्शाइये कि -
(gof)−1=f−1og−1 हैं ।
View Solutionf:{1,2,3}→{a,b,c} तथा g:{a,b,c}→{सेब ,गेंद ,बिल्ली}f(1)=a,f(2)=b,f(3)=c,g(a)= सेब , g(b) = गेंद तथा g( c ) = बिल्ली द्वारा परिभाषित फलनों पर विचार कीजिए कि f,g और gof व्यूत्क्रमणीय है । f−1,g−1 तथा (gof)−1 ज्ञात कीजिए तथा प्रमाणित कीजिए कि (gof)−1=f−1og−1 है ।
View Solutionयदि f तथा g इस प्रकार परिभाषित हैं कि f(x)=x2+2 तथा g(x)=1−1x , तो gof तथा fog ज्ञात कीजिए।
View Solutionयदि f तथा g दो फलन निम्न प्रकार से परिभाषित हैं :
f(x)=xx−1 तथा g(x)=1x−3 जहाँ x∈R तो gof तथा fog ज्ञात कीजिए तथा उनके डोमेन भी लिखिए ।
View Solutionयदि फलन f तथा g निम्न प्रकार परिभाषित हो, तो fog तथा gof ज्ञात कीजिए:
f(x)=logx,g(x)=ex
View Solutionयदि फलन f तथा g निम्न प्रकार परिभाषित हो, तो fog तथा gof ज्ञात कीजिए:
f(x)=x3,g(x)=sinx
View Solutionयदि फलन f तथा g निम्न प्रकार परिभाषित हो, तो fog तथा gof ज्ञात कीजिए:
f(x)=cosx,g(x)=|sinx|
View Solutionयदि फलन f तथा g निम्न प्रकार परिभाषित हो, तो fog तथा gof ज्ञात कीजिए:
f(x)=ex,g(x)=x+2
View SolutionConsider as f(1)=a,f(2)=b,f(3)=c,
g:[a,b,c]→ {apple, ball, cat}
Defined as f(1)=a,f(2)=b,f(3)=c,
g(a) = apple, g(b) = ball, g(c ) = cat
Show that f, g and gof are invertible.
Find f−1,g−1 and (gof)−1 and show that :
(gof)−1=f−1og−1.
View SolutionConsider f:{1,2,3}→{a,b,c}andg:{a,b,c}→{apple, ball, cat} defined as f(1)=a,f(2)=b,f(3)=c,g(a) = apple,g(b)= ball and g (c )= cat. Show that f, g and gof are invertible. Find out f−1,g−1and(gof)−1 and show that (gof)−1=f−1og−1.
View SolutionConsider f:{1,2,3}→{a,b,c}andg:{a,b,c}→{apple, ball, cat} defined as f(1)=a,f(2)=b,f(3)=c,g(a) = apple,g(b)= ball and g (c )= cat. Show that f, g and gof are invertible. Find out f−1,g−1and(gof)−1 and show that (gof)−1=f−1og−1.
View Solution
