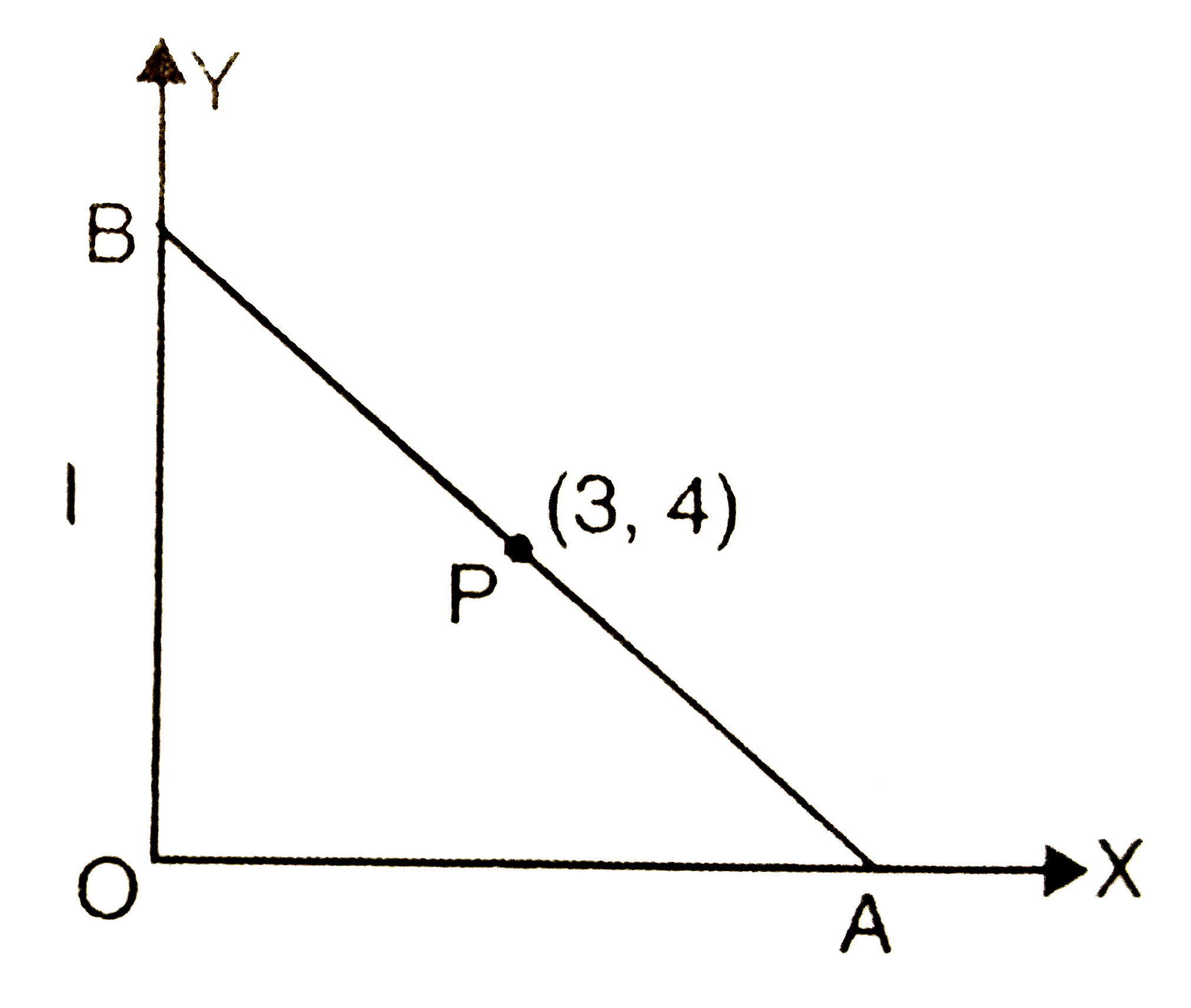
बिंदु (3,4) से जाती हुई सरल रेखा का समीकरण निकालें जो प्रथम पाद से न्यूनतम क्षेत्रफल का त्रिभुज काटता है|
माना की बिंदु P(3,4) से जाती हुई सरल रेखा AB है|
P(3,4) से जाती हुई किसी रेखा का समीकरण होगा,
y−4=m(x−3) ...(1)
(1 ) में y =0 रखने पर, x=3−4m मिलता है|
अतः रेखा x अक्ष को A(3−4m,0) पर काटता है|
तथा x =0 रखने पर ,y =4 -3m
अतः रेखा y अक्ष के B(0,4−3m) पर काटता है|
अब ΔOAB का क्षेत्रफल A=12(3−4m)(4−3m)
m के सापेक्ष अवकलित करने पर हमें मिलता है,
dAdm=12(4m2)(4−3m)+12(3−4m)(−3)
=8−6mm2+3⋅4−3m2m=16−9m22m2 ...(3)
A के महत्तम या न्यूनतम मान के लिए
dAdm=0⇒9m2=16⇒m=±43
साथ ही d2Adm2=16m3
जब m=43 तो d2Adm2<0 ∴A महत्तम है|
जब m=−43 तो d2Adm2>0 ∴A न्यूनतम है|
अब ΔAOB का क्षेत्रफल न्यूनतम होने के लिए m=−43
∴ (1 ) से रेखा का अभीष्ट समीकरण है, y−4=−43(x−3)
⇒3y−12=−4x+12 ⇒4x+3y=24
(##KCS_HIN_MAT_XII_P1_C18_SLV_026_S02.png" width="80%">
Topper's Solved these Questions
- उच्चतम और निम्नतम BOOK - KC SINHACHAPTER - उच्चतम और निम्नतम EXERCISE - प्रश्नावली 18.1
69 Videos
- आव्यूहBOOK - KC SINHACHAPTER - आव्यूहEXERCISE - OBJECTIVE QUESTIONS
23 Videos
- त्रिविमीय ज्यामिति दो रेखाओ के बीच का कोण BOOK - KC SINHACHAPTER - त्रिविमीय ज्यामिति दो रेखाओ के बीच का कोण EXERCISE - अभ्यास 28.1
18 Videos
Similar Questions
निम्नलिखित फलन के सभी स्थानीय उच्चतम मान और न्यूनतम बिंदुओं , यदि कोई हो तो ज्ञात कीजिए तथा संगत उच्चतम और निम्नतम मान भी ज्ञात कीजिए| f(x)=x3−6x2+9x+15
View SolutionX और y के दिए गए मानों में से कौन-सा जोड़ा निम्न जोड़े को समान बनाता है [3x+75y+12−3x][0y−28 4]
View Solutionयदि एक रेखा x ,y तथा z -अक्ष कि धनात्मक दिशा के साथ क्रमशः 90∘,60∘,30∘ का कोण बनती है तो इसकी दिक्-कोसाइन ज्ञात कीजिए.
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखाओ x=−3 तथा x=5 से समान दूरी पर है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए ,जो रेखाये x−y−6=0 तथा 7x−5y=36 के प्रतिच्छेद बिंदु को मूलबिंदु से मिलती है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो रेखा 7x−5y+14=0 के समान्तर है तथा रेखाओ 2x+3y+7=0 और 3x−4y−15=0 के प्रतिच्छेद बिंदु से होकर जाती है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु (−1,5) से होकर जाती है ओर यह बिंदु उसके द्वारा 3:2 अक्षो के बीच कटे हुए भाग को 3:2 के अनुपात में विभाजित करता है
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिंदु(1,2) से होकर जाती है जिसके द्वारा अक्षो से बने त्रिभुज का क्षेत्रफल 92 वर्ग इकाई है
View Solutionसरल रेखा x−12=y−21=z+3−3 के समांतर उस रेखा के समीकरण ज्ञात कीजिए जो मूल बिंदु से होकर जाती है।
View Solutionउस समतल का समीकरण ज्ञात कीजिए, जो अक्षों से समान अन्तःखण्ड काटता है तथा बिंदु (2, 3, 4) से होकर जाता है |
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (3,-4) से होकर जाती है और अक्षों से बराबर परन्तु विपरीत चिन्हो के अन्तः खण्ड काटती है ।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (1,2) से होकर जाती है और y -अक्ष से ऐसा अन्तः खण्ड काटती है जो कि x -अक्ष पर काटे अन्तः खण्ड को दो गुना है।
View Solutionउस रसाल रेखा का समीकरण ज्ञात कीजिए जो अक्षो पर समान अन्तः खण्ड काटे तथा रेखा अक्षो से घिरे त्रिभुज का क्षेत्रफल 8 वर्ग मात्रक हो।
View Solutionबिंदु (1,2,3) से गुजरने वाली तथा दिक् अनुपात 4,5,6 वाली सरल रेखा का समीकरण ज्ञात कीजिए।
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (a,b,c) से होकर जाती है तथा Y-अक्ष के समान्तरहै।
View Solutionसमतल का समीकरण जो अक्षो से इकाई लम्बाई का अन्तः खंड काटता है -
View Solution
