[Find the value of ] ∫π0|cosx−sinx|dx का मान ज्ञात करे |
cosx−sinx=0⇒cosx=sinx⇒tanx=1=tan.Π4
∴x=nπ+π4, जहाँ n=0,±1,±2,… जिसमे से केवल π4,0 और π के बीच है ।
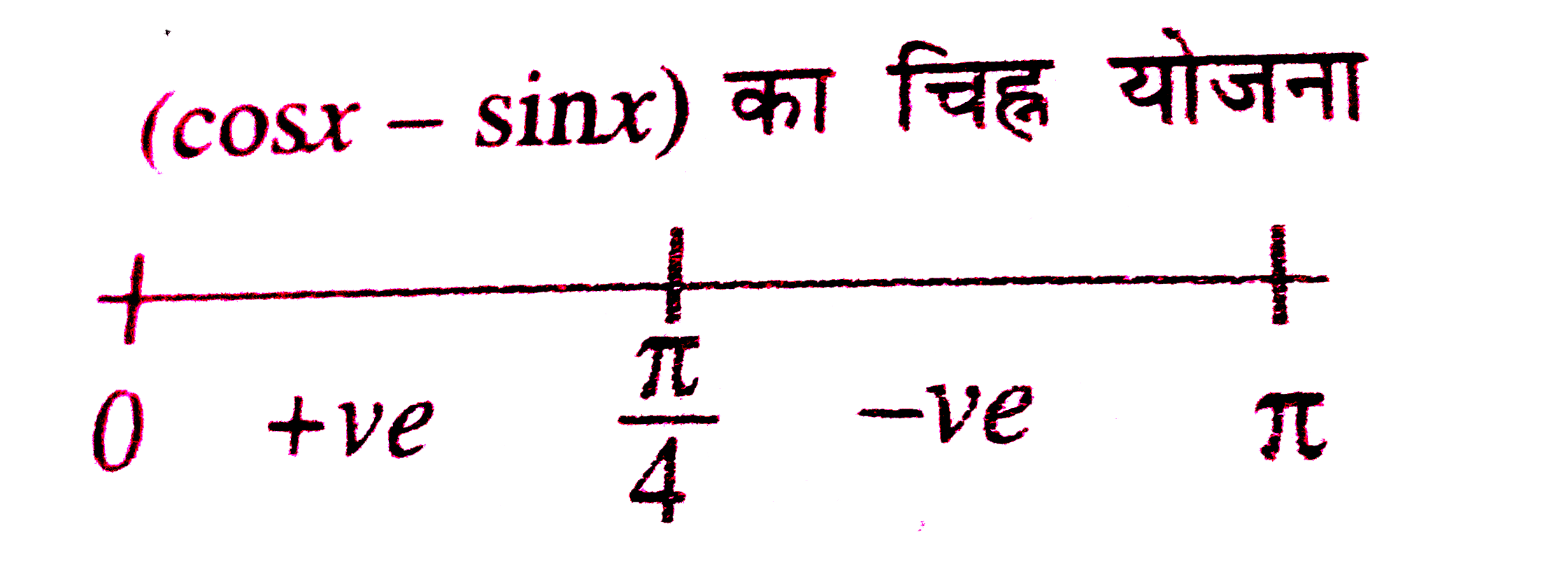
अब I=∫π0|cosx−sinx|dx
=∫π/40|cosx−sinx|dx+∫ππ/4|cosx−sinx|dx
=∫π/40(cosx−sinx)dx−∫ππ/4(cosx−sinx)dx
=[sinx+cosx]π/40−[sinx+cosx]ππ/4
=[(sin.π4+cos.π4)−(sin0+cos0)]
−[(sinπ+cosπ)−(sin.π4+cos.π4)]
=[(1√2+1√2−1)]−[(0−1)−(1√2+1√2)]
√2−1−(−1−√2)=√2−1+1+√2=2√2
Topper's Solved these Questions
- निश्चित समाकलों के गुणधर्म BOOK - KC SINHACHAPTER - निश्चित समाकलों के गुणधर्म EXERCISE - अभ्यास 21.1
65 Videos
- निश्चित समाकलों के गुणधर्म BOOK - KC SINHACHAPTER - निश्चित समाकलों के गुणधर्म EXERCISE - अभ्यास 21.2
26 Videos
- द्वितीय कोटि का अवकलज BOOK - KC SINHACHAPTER - द्वितीय कोटि का अवकलज EXERCISE - OBJECTIVE QUESTIONS
5 Videos
- प्रतिलोम त्रिकोणमितीय फलन BOOK - KC SINHACHAPTER - प्रतिलोम त्रिकोणमितीय फलन EXERCISE - अभ्यास 4.1
76 Videos
Similar Questions
निम्नलिखित को ज्ञात करे ।
(i) ∫2−2|x|dx
View Solutionयोगफल कि सीमा के रूप में निम्नलिखित समाकलों के मान ज्ञात कीजिये ।
(i) ∫20xdx
View SolutionIf x=a(cosθ+θsinθ),y=a(sinθ−θcosθ), then d2ydx2=
View Solutionमान निकालें :
sin−1(√32)
View SolutionEvaluate : ∫π20(sinx+cosx)dx
View SolutionEvaluate: ∫π20|sinx−cosx|dx
View Solutionint_ (0) ^ ((pi) / (2)) (sin x) / (sin x + cos x) dx = int_ (0) ^ ((pi) / (2)) (cos x) / (sin x + cos x) dx = int_ (0) ^ ((pi) / (2)) (dx) / (1 + cot x) = int_ (0) ^ ((pi) / (2)) (dx) / ( 1 + time x) = (pi) / (4)
View SolutionThe value of int_(0)^(2 pi)|cos x-sin x|dx is
View Solution∫xsin3x2cosx2dx का मान ज्ञात कीजिए।
View Solution∫π/20sin4xcos4x+sin4xdx का मान ज्ञात कीजिए।
View Solution(i) ∫π0xdx1+sinx का मान ज्ञात कीजिये।
(ii) ∫π/20sinx−cosx1+sinxcosxdx का मान ज्ञात कीजिये।
View Solution∫π/20sin2xsinx+cosxdx का मान ज्ञात कीजिये।
View Solutionमान ज्ञात कीजिए ∫π/20cosx(1+sinx)(2+sinx)dx.
View Solution∫π/20sin4x(sin4x+cos4x)dx का मान ज्ञात कीजिएः
View Solution∫π/20sinx−cosx1+sinxcosxdxका मान ज्ञात कीजिएः
View Solutionlimx→πsin(π−x)π(π−x) का मान ज्ञात कीजिए ।
View Solution
