ज्ञात करे[ Evalute] ∫3/2−1|xsinπx|dx
यहाँ |xsinπx| आता है इसलिए सर्वप्रथम x हम πx का अंतराल [−1,32] में चिन्ह योजना लिखते है ।
अब , xsinπx=0⇒x=0 ,sinπx=0
⇒x=0 या πx=nπ
⇒x=0 याx=n,n=0,±1,±2....
⇒x=0 या x=0,1अंतराल (−1,32) में
यहाँ 0 दो बार आता है ।
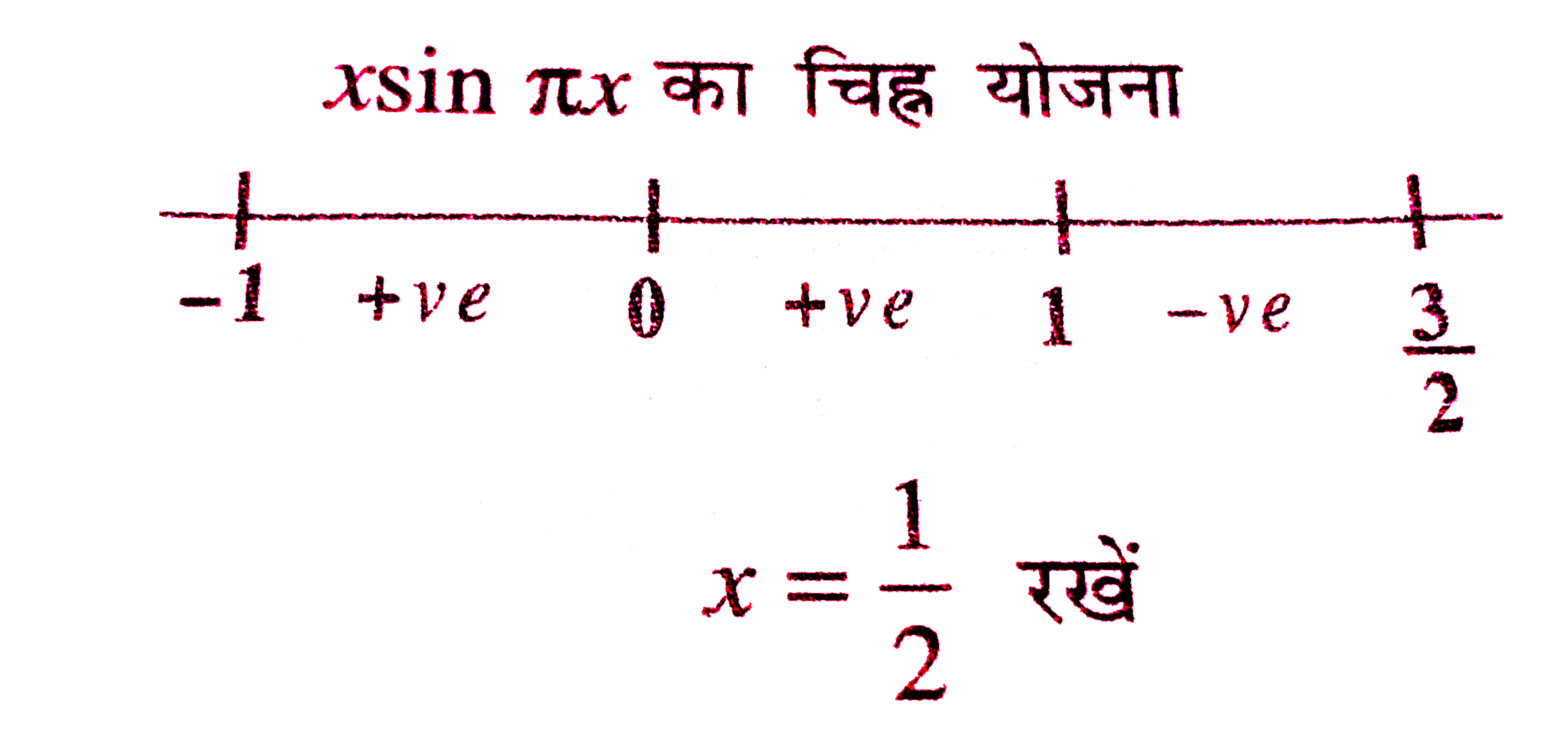
अब ∫3/2−1|xsinπx|dx=∫1−1|xsinπx|dx+∫3/21|xsinπx|dx
=∫1−1xsinπxdx+∫3/21(−xsinπx)dx=∫1−1xsinπxdx−∫3/21xsinπxdx
=2∫10xsinπxdx−∫3/21xsinπxdx [∵xsinπx एक सम फलन है । ]
अब ∫xsinπ x dx=−xπcosπx+1x∫cosπ x dx=−xπcosπx+1x2sinπx
∴∫3/21|xsinπx|dx
=2[−xπcosπx+1π2sinπx]10−[−xπcosπx+1π2sinπx]3/21
=2[(1πcosπ+1π2sinπx)−(0)]
−[(−32πcos.3π2+1π2sin.3π2)−(−1πcosπ+1π2sinπ)]
=2[(1π+0)]−[0+1π2.(−1)−(1π+0)]=2π+1π2+1π=3π+1π2
Topper's Solved these Questions
- निश्चित समाकलों के गुणधर्म Book:KC SINHAChapter:निश्चित समाकलों के गुणधर्म Exercise:अभ्यास 21.1
Explore 65 Videos
- निश्चित समाकलों के गुणधर्म Book:KC SINHAChapter:निश्चित समाकलों के गुणधर्म Exercise:अभ्यास 21.2
Explore 26 Videos
- द्वितीय कोटि का अवकलज Book:KC SINHAChapter:द्वितीय कोटि का अवकलज Exercise:OBJECTIVE QUESTIONS
Explore 5 Videos
- प्रतिलोम त्रिकोणमितीय फलन Book:KC SINHAChapter:प्रतिलोम त्रिकोणमितीय फलन Exercise:अभ्यास 4.1
Explore 76 Videos
Similar Questions
निम्नलिखित को ज्ञात करे ।
(i) ∫2−2|x|dx
View Solutionयोगफल कि सीमा के रूप में निम्नलिखित समाकलों के मान ज्ञात कीजिये ।
(i) ∫20xdx
View SolutionIf x=a(cosθ+θsinθ),y=a(sinθ−θcosθ), then d2ydx2=
View Solutionमान निकालें :
sin−1(√32)
View Solution∫32_(−1)|xsin(πx)|dx==
View SolutionEvalute the following integrals
∫11+sinx dx
View SolutionEvalute the following integrals
∫sinx1+sin xdx
View SolutionEvalute the following integrals
∫2cos3x+3sin3xsin2xcos2x dx
View SolutionEvalute the following integrals
∫√1+sin2xdx,x∈[−π2,π2]
View SolutionEvalute the following integrals
∫11+sin2x dx
View SolutionEvalute the following integrals
∫sinxsin(a+x) dx
View SolutionEvalute the following integrals
∫14sin2x+3sin x cos x +2cos2x dx
View SolutionEvalute the following integrals
∫12+3 sin x dx
View SolutionEvalute the following integrals
∫exsin2x dx
View SolutionEvalute the following integrals
∫sin−1 x dx on (-1, 1)
View SolutionEvalute the following integrals
∫x3−1x2 dx
View Solution
