ताश के 52 पत्तो की एक भली-भाँति फेंटी हुई गड्डी में से दो पत्ते उत्तरोत्तर बिना प्रतिस्थापना के निकाले जाते है। इक्को के निकालने की संख्या के लिए प्रसरण का परिकलन कीजिए।
माना कि Ai, iवे खिंचाव में इक्का आने की घटना को सूचित करता है, जहाँ I = 1, 2 पुनः माना कि X दो खिंचाव में इक्का आने की संख्या को सूचित करता है। तब X के संभावित मान 0, 1, 2 है।
अब P(X=0) = दो लगातार खिंचाव में कोई इक्का नहीं आने घटना
=P(¯¯¯A1∩¯¯¯A2)=P(¯¯¯A1)P(¯¯¯A2/¯¯¯A1)=4852×4751=564663
P(X = 1) = दो लगातार खिंचाव में एक इक्का आने की घटना
=P[(A1∩¯¯¯A2)∪(¯¯¯A1∩A2)]
=P(A1∩¯¯¯A2)+P(¯¯¯A1∩A2) [∵A1∩¯¯¯A2 और (¯¯¯A1∩A2) परस्पर अपवर्जी घटनाएँ है।]
=P(A1)P(¯¯¯A2/A1)+P(¯¯¯A1)P(A2/¯¯¯A1)
=452×4851+4852×451=96663
P (X=2) = प्रत्येक खिंचाव में एक इक्का आने की घटना
=P(A1∩A2)=P(A1)P(A2/A1)=452×351=3663
अतः X के लिए अभीष्ट प्रायिकता वितरण निम्नलिखित है :
X=(xi)012P(X)=(pi)564663966633663
∴Σpixi=0×564663+1×96663+2×3663=102663
तथा Σpix2i=564663×0+96663×1+3663×4=108663
अतः var.(X)=Σpix2i−(Σpixi)2
=108663−(102663)2=108×663−102×102(663)2=61200663×663=4002873
Topper's Solved these Questions
- यादृच्छिक चर और प्रायिकता बंटन BOOK - KC SINHACHAPTER - यादृच्छिक चर और प्रायिकता बंटन EXERCISE - अभ्यास 34.1 Type I.
7 Videos
- यादृच्छिक चर और प्रायिकता बंटन BOOK - KC SINHACHAPTER - यादृच्छिक चर और प्रायिकता बंटन EXERCISE - अभ्यास 34.1 Type II.
16 Videos
- बरनौली परीक्षण और द्विपद बंटन BOOK - KC SINHACHAPTER - बरनौली परीक्षण और द्विपद बंटन EXERCISE - OBJECTIVE QUESTIONS
10 Videos
- रैखिक प्रोग्रामनBOOK - KC SINHACHAPTER - रैखिक प्रोग्रामनEXERCISE - OBJECTIVE QUESTIONS
5 Videos
Similar Questions
X012P(X)0.20.60.2
View Solutionदो सिक्को के एक साथ उछाल में यादृच्छिक चर पटो की संख्या X का प्रायिकता बंटन ज्ञात कीजिए।
View SolutionIn a box containing 100 bulbs , 10 are defective. What is the probability that out of a sample of 5 bulbs, none is defective ?
View SolutionThe corner pont sof the feasible region determined by the followign system of linear inequalities :2x+y≤10,x+3y≤15,xy≥0 are (0,0),(5,0),(3,4) and (0,5). Let Z=px+qy where p,q≥0. Conditions on p and q so that the maximum of Z occurs at both (3,4) and (0,5) is
View Solution52 पत्तो की एक भाँति फेंटी गई गड्डी में एक पत्ता खो जाता है। शेष पत्तो से दो पत्ते निकाले जाते है नो ईंटके पत्ते है । खो गए पत्ते के ईंट का पत्ता होने की प्रायिकता है ?
View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
View Solutionताश के 52 पत्तो की एक सुनिश्चित गड्डी में से एक पत्ता यदृच्छया निकाला जाता है | यदि
E : निकाला गया पत्ता हुकुम का है |
F : निकाला गया पत्ता इक्का है , तो E तथा F घटनाएँ है -
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionदो अंको की एक संख्या में इकाई स्थान का अंक दहाई स्थान के अंक से 3 अधिक है यदि दोनों अंकों का जोड़ 11 हो तो संख्या निकालिए।
View Solutionअच्छी प्रकार से फेटी हुई 52 ताशों की एक गड्डी में से 1 बादशाह प्राप्त करने की प्रायिकता ज्ञात कीजिए।
View Solution1 की भूमिका#!# एक संख्या का ऋणात्मक #!# व्युत्क्रम #!#परिमेय संख्याओं के लिए गुणन की वितरकता
View Solutionवायु के आधिक्य में सोडियम के दहन से एक उच्च ऑक्साइड प्राप्त होता है । उत्पाद में ऑक्सीजन की ऑक्सीकरण अवस्था क्या है ? ऋणात्मक चिन्ह की उपेक्षा कीजिए ।
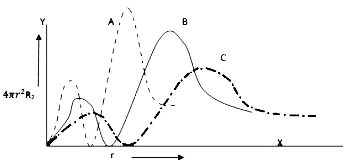
View Solutionनिम्नलिखित में से कौन सा, 2s कक्षक के लिए इलेक्ट्रॉन के पाये जाने की अरीय प्रायिकता का सही मिलान है
View SolutionM के लिए विद्यमान त्रिविम समावयवियों की कुल संख्या है:
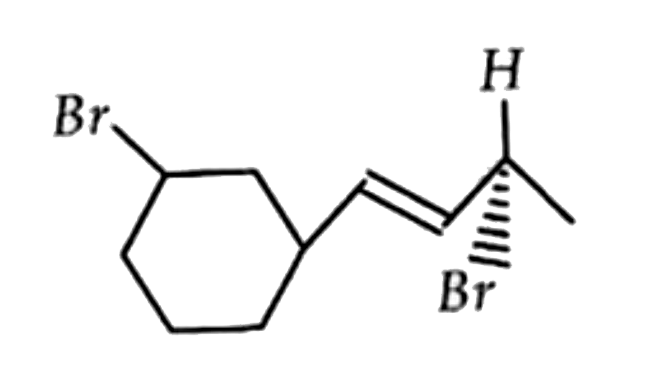
View Solutionअणु के लिए संभव त्रिविम समावयवी की संख्या है
View Solutionसीरियम (Z = 58) लैंथेनॉइडों का एक सदस्य है। निम्नलिखित में से सीरियम के बारे में गलत कथनों की पहचान कीजिए।
View Solution
