निम्नलिखित का गुणनखंड निकाले :
a2+b2+2(ab+bc+ca)
a2+b2+2(ab+bc+ca)
=a2+b2+2ab+2bc+2ca+c2−c2
=a2+b2+c2+2ab+2bc+2ca−c2
=(a+b+c)2−c2
=(a+b+c+c)(a+b+c−c)
=(a+b+2c)(a+b)
दूसरी विधि : a2+b2+2(ab+bc+ca)
=a2+b2+2ab+2bc+2ca
=(a+b)2+2c(b+a)
=(a+b)(a+b+2c)
Topper's Solved these Questions
- BOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - साधित उदाहरण19videos
बीजीय सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - अभ्यास -4.123videos
बीजीय सर्वसमिकाएँ
- BOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - दीर्घ उत्तरीय प्रश्न3videos
प्रायिकता या सम्भावित
- BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - वस्तुनिष्ठ प्रश्न15videos
यूक्लिड की ज्यामितीय का परिचय
Similar Questions
निम्नलिखित में से प्रत्येक का गुणनखंड कीजिए
27y3+125z302:16View Solutionउपयुक्त सर्वसमिकाओ का उपयोग कर निम्नलिखित गुणनफल ज्ञात कीजिए:
(x+3)(x+3)08:21View Solution70 विद्यार्थी के प्राप्ताकों का विवरण नीचे तालिका में दिया गया है।
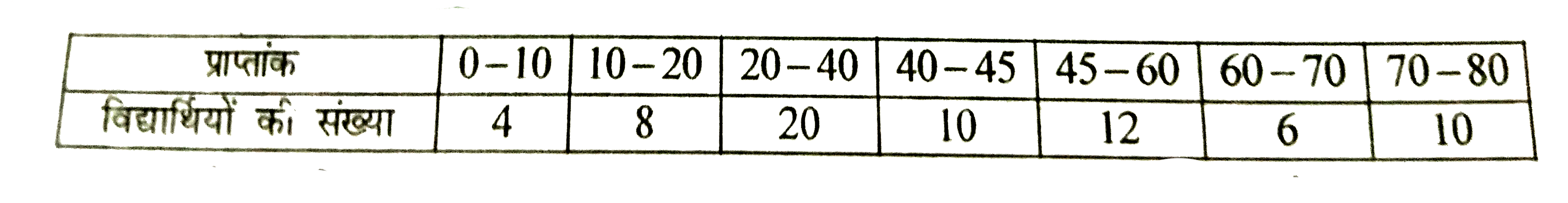
एक विद्यार्थी द्वारा निम्नलिखित वर्ग-अन्तराओं के बीच प्राप्तांकों की प्रायिकता ज्ञात करें।
(i) 0-20 (ii) 0-60View Solutionएक बिंदु से होकर कितनी रेखाएँ खींची जा सकती हैं ?
06:08View Solutionshow that the determinant
∣∣ ∣ ∣∣a2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2∣∣ ∣ ∣∣
is always non- negative.06:21View Solution∣∣ ∣ ∣∣ a2 bcc2+caa2+ab b2 ca abb2+bc c2∣∣ ∣ ∣∣=4a2b2c2
02:30View Solution∣∣ ∣ ∣∣(a+b)2cabcca(b+c)2abbcab(c+a)2∣∣ ∣ ∣∣=
08:23View Solution∣∣ ∣ ∣∣a2+x2abcaabb2+x2bccabcc2+x3∣∣ ∣ ∣∣= का भाजक है
03:05View Solutionপ্রমাণ করো যে, ∣∣ ∣ ∣∣abca2b2c2bccaab∣∣ ∣ ∣∣=(a−b)(b−c)(c−a)(ab+bc+ca)
01:16View SolutionIf ab+bc+ca=0, then the value of 1a2−bc+1b2−ca+1c2−ab will be :
07:05View Solutionयदि a,b,c ∈ R तब सारणिक △∣∣ ∣ ∣∣a2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2∣∣ ∣ ∣∣ अऋणांत्मक होगा पुनः सारणिक के शून्य होने के सार्थ बताये
07:02View Solutionshow that the determinant
∣∣ ∣ ∣∣a2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2bc+ca+abbc+ca+abbc+ca+aba2+b2+c2∣∣ ∣ ∣∣
is always non- negative.03:09View SolutionIf ab + bc + ca = 0, then the value of 1a2−bc+1b2−ca+1c2−ab will be:
02:30View SolutionProve that ∣∣ ∣ ∣∣abca2b2c2bccaab∣∣ ∣ ∣∣=(a−b)(b−c)(c−a)(ab+bc+ca)
01:16View SolutionProve that : ∣∣ ∣ ∣∣abca2b2c2bccaab∣∣ ∣ ∣∣=(a−b)(b−c)(c−a)(ab+bc+ca)
02:39View Solutionshow that the determinant |{:(a^(2)+b^(2)+c^(2),,bc+ca+ab,,bc+ca+ab),(bc+ca+ab,,a^(2)+b^(2)+c^(2),,bc+ca+ab),(bc+ca+ab,,bc+ca+ab,,a^(2)+b^(2)+c^(2)):}| is always non- negative.
02:08View Solution

