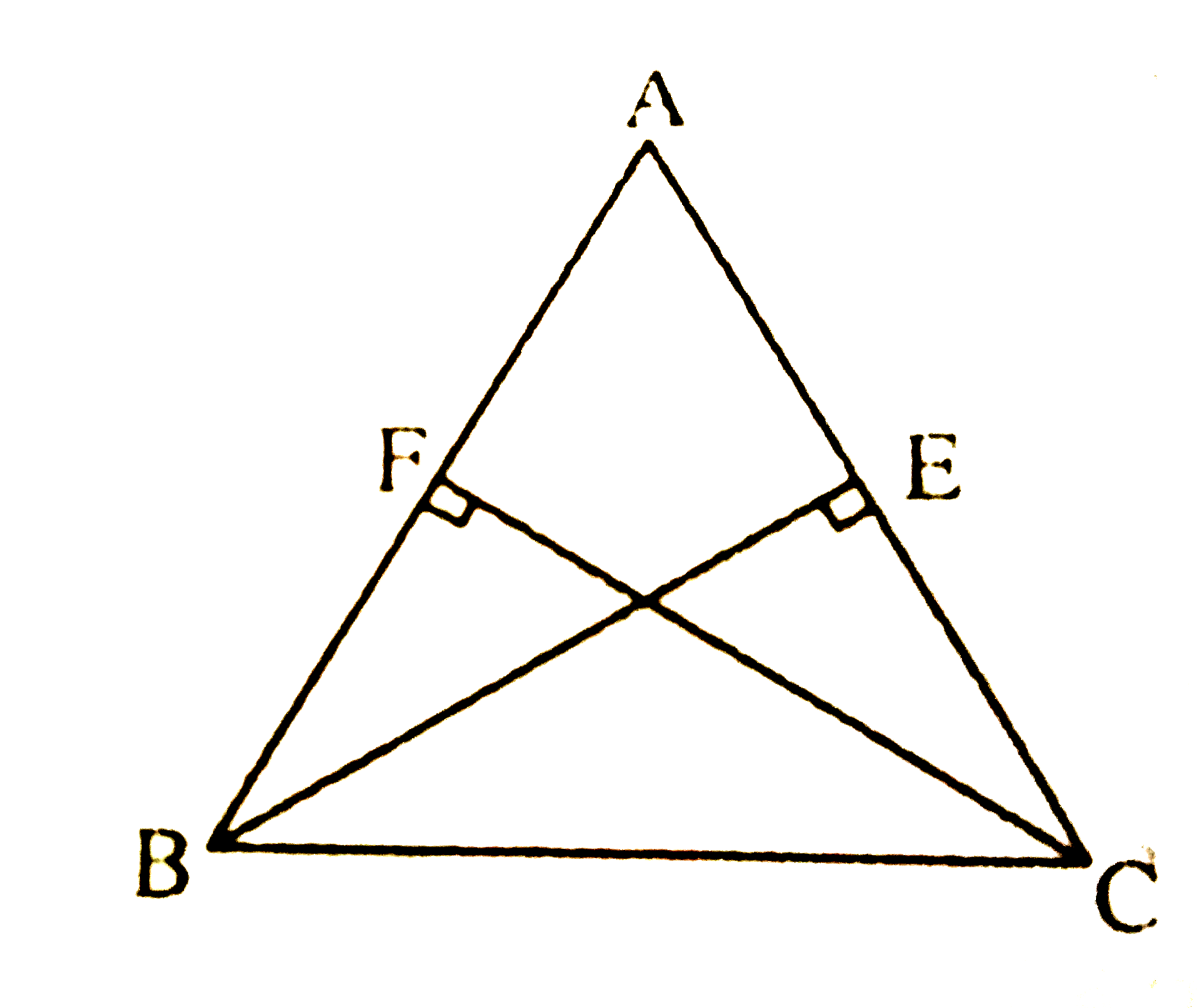
BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं | RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है |
दिया है : ABC एक त्रिभुज है जिसमें तथा BE⊥AC तथा CF⊥AB तथा BE=CF
सिद्ध करना है कि ΔABC समद्विबाहु है अर्थात AB = AC.
प्रमाण : ΔBEC तथा ΔCFB में,
∠BEC=∠CFB=90∘
BC=BC [उभयनिष्ठ]
तथा BE=CF [दिया है]
अत: ΔBEC≅ΔCFB [RHS सर्वांगसमता नियम से]
∴ ∠ECB=∠FBC
⇒ ∠C=∠B
⇒ AB=AC
Topper's Solved these Questions
- त्रिभुजों की सर्वांगसमता BOOK - KC SINHACHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास 9.1 (अतिलघु उत्तरीय प्रश्न )
36 Videos
- त्रिभुजों की सर्वांगसमता BOOK - KC SINHACHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - अभ्यास 9.1 लघु उत्तरीय प्रश्न
11 Videos
- ज्यामितीय बनावट ( रचनाएँ ) BOOK - KC SINHACHAPTER - ज्यामितीय बनावट ( रचनाएँ ) EXERCISE - उदाहरण
11 Videos
- दो चरों वाले रैखिक समीकरण BOOK - KC SINHACHAPTER - दो चरों वाले रैखिक समीकरण EXERCISE - वस्तुनिष्ट प्रश्न
15 Videos
Similar Questions
यदि किसी त्रिभुज की दो भुजाएँ और उनके .............. कोण, दूसरे त्रिभुज की तदनुरूपी दोनों भुजाओं तथा उनके अंतर्गत कोण के बराबर हों तो दोनों त्रिभुज सर्वांगसम होते हैं |
View Solutionदो त्रिभुजों के सर्वांगसम होने के लिए भुजा-भुजा-भुजा प्रतिबंध को लिखें |
View Solutionएक △ABC बनाये जिसमे BC या (a) =6.6सेमि, CA+AB या (b+c) =10.2 सेमि तथा ∠B=60∘
View Solutionएकघातीय समीकरण ax+by+c=0 के वास्तविक हलो की संख्या है
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है । यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2)है , तो त्रिभुज की शेष दो भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि ΔABC एक समद्विबाहु त्रिभुज है यदि
∣∣ ∣ ∣∣1111+cosA1+cosB1+cosCcos2A+cosAcos2B+cosBcos2C+cosC∣∣ ∣ ∣∣=0
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
View Solutionसदिशों के प्रयोग द्वारा उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A(2,3,5),B(3,5,8) और C(2,7,8) हैं |
View Solutionएक समकोण समद्विबाहु त्रिभुज के कर्ण का समीकरण 3x+4y=4 है। यदि इसके सम्मुख शीर्ष के निर्देशांक (2,2) हो तो त्रिभुज की शेष दो भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,5), (6,3) और (5,10)
View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(1,1), (-1,-1) और (−√3,√3)
View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,0), (5,5√3) और (−5,5√3)
View Solutionत्रिभुज के शीर्षलम्ब
View Solutionएक त्रिभुज की दो भुजाओं की मापों का योग
View Solution
