ΔABC और ΔDEF में AB=DE,AB∣∣DE,BC=EF और BC∣∣EF है। शीर्षों A,B,C को क्रमशः शीर्षों D,E,F से जोड़ा जाता है। दर्शाइए कि
(i) चतुर्भुज ABED एक समांतर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है।
(iii) AD∣∣CF और AD=CF है।
(iv) AC=DF है।
(v) चतुर्भुज ACFD एक समांतर चतुर्भुज है।
(vi) ΔABC≅ΔDEF है।
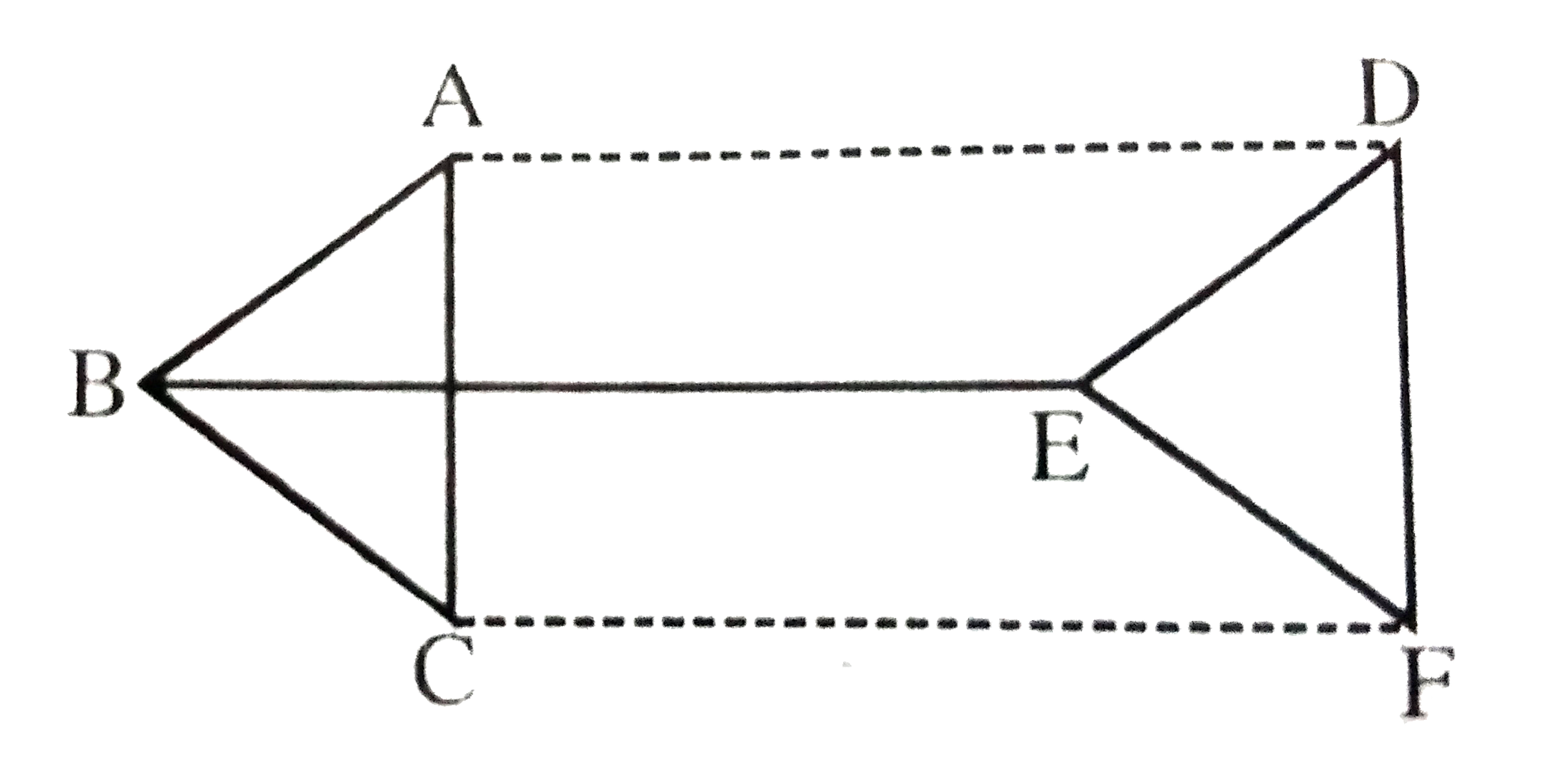
(i)दिया है :AB∣∣DE तथा AB=DE
∴ABED एक समांतर चतुर्भुज है।
अतः AD∣∣BE तथा AD=BE …..ii
∵BC∣∣EF तथा BC=EF
(ii) ∴BEFC एक समांतर चतुर्भुज है।
∵BCFE एक समांतर चतुर्भुज है।
अतः BE∣∣CF तथा BE=CF
(iii) समीकरण (i) और (ii) से
∵AD∣∣CF तथा AD=CF
(iv) (iii) में हम सिद्ध कर चुके है। कि AD∣∣CF तथा AD=CF
∴ACFD एक समांतर चतुर्भुज है। ………….iii
(v) अतः ACFD एक समांतर चतुर्भुज है।
AC∣∣DF तथा AC=DF
(v) अब ΔABC तथा ΔDEF में
AC=DF [ ∵ACFD एक समांतर चतुर्भुज है]
AB=DE [ ∵ABED एक समांतर चतुर्भुज है]
तथा BC=EF[ ∵BCFE एक समांतर चतुर्भुज है]
अतः ΔABC≅De<ADEF [SSS सर्वांगसमता नियम से]
Topper's Solved these Questions
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - अतिलघु उत्तरीय प्रश्न (समांतर चमुर्भुज, आयत, वर्ग तथा समचतुर्भुज से संबंधित परिभाषाओं, प्रमेयों तथा उपप्रमेयों के सीधे प्रयोग पर आधारित प्रश्नः)
16 Videos
- समांतर चतुर्भुजBOOK - KC SINHACHAPTER - समांतर चतुर्भुजEXERCISE - लघु उत्तरीय प्रश्न
4 Videos
- वृत्त BOOK - KC SINHACHAPTER - वृत्त EXERCISE - वस्तुनिष्ठ प्रश्न
17 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - KC SINHACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - वस्तुनिष्ट प्रश्न
7 Videos
Similar Questions
रिक्त स्थानों को भरें:
कोई समांतर चतुर्भुज एक समचतुर्भुज होगा यदि और केवल यदि उसके...................... एक-दूसरे पर लम्ब हो।
View Solutionकिसी समांतर चतुर्भुज ABCD में ∠D=110∘ तो ∠A एवं ∠B की माप अंशों में लिखें।
View Solutionवृत्त पर किन्ही दो बिन्दुओं को मिलाने वाली रेखाखंड को क्या कहते है ?
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View SolutionIn ΔABC and ΔDEF, AB= DE, AB || DE, BC= EF and BC|E|F. Vertices A, B and C are joined to vertices D, E and F respectively. Show that
AD|C|F and AD = CF
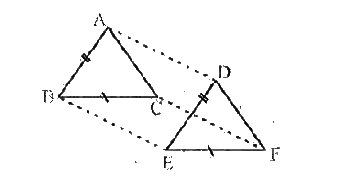
View SolutionIn ΔABCandΔDEF,AB=DE,AB||DE,BC=EFandBC||EF Vertices A,B and C are joined to vertices D , E and F respectively show that
quadrilateral ABED is a parallelogram
quadrilateral BEFC is a parallelogram
AD∣∣CFandAD=CF
quadrilateral ACFD is a parallelogram
AC=DF
ΔABC≈ΔDEF.
View Solutionनिम्नलिखित के उत्तर दीजिए और उनके कारण भी दीजिए :
(i ) क्या AB = BC है?
(ii ) क्या AB = DC है?
(iii ) क्या DE = AF है?
(iv ) क्या EF = AB है?
(v ) क्या BC = EF है?
(vi ) क्या AB = DC = EF है?
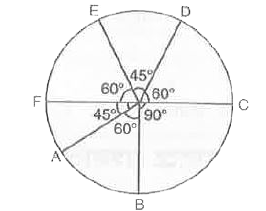
View SolutionRevision|चतुर्भुज#!#समांतर चतुर्भुज#!#महत्वपूर्ण प्रश्न
View SolutionThe length of two sides of a parallelogram are 3cm and 10 cm. What is the sum of the squares of diagonals of the parallelogram ? एक समांतर चतुर्भुज के दो भुजाओं की लंबाई 3 सेमी और 10 सेमी है। समांतर चतुर्भुज के विकर्णों के वर्गों का योग क्या होगा ?
View SolutionABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=160∘. What is the measure of the ∠BAC ?
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इसे घेरने वाले वृत्त का व्यास है और ∠ADC=160∘ है | कोण BAC का माप क्या है ?
View SolutionA circle inscribed in a triangle ABC touches its sides AB, BC and AC at the points D, E and F, respectively. If AB = 18cm, BC = 15cm and AC = 13 cm then the value of of AD+BE+CF is: एक त्रिभुज ABCमें अंकित एक वृत्त क्रमशः AB, BC और AC के भुजाओं D, E और F को स्पर्श करता है। यदि AB = 18 सेमी, BC = 15 सेमी और AC = 13 सेमी है तो AD+ BE+ CF का मान है:
View Solutionचतुर्भुज |चतुर्भुज का कोण योग गुण |चतुर्भुज के प्रकार |समांतर चतुर्भुज के गुण|प्रमेय|सारांश
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE||BC and AD/BD=3/4 . The ratio of the area of triangle ABC to the area of trapezium DECB is: त्रिभुज ABC में, AB और AC भुजाओं पर 2 बिंदु क्रमशः D और E इस तरह है कि DE||BC और AD/BD=3/4 है| triangle ABC क्षेत्रफल का समलंब चतुर्भुज DECB के क्षेत्रफल से अनुपात है :
View Solutionसमांतर चतुर्भुज कअ क्षेत्रफल
View Solutionसमांतर चतुर्भुज के गुण
View Solution
