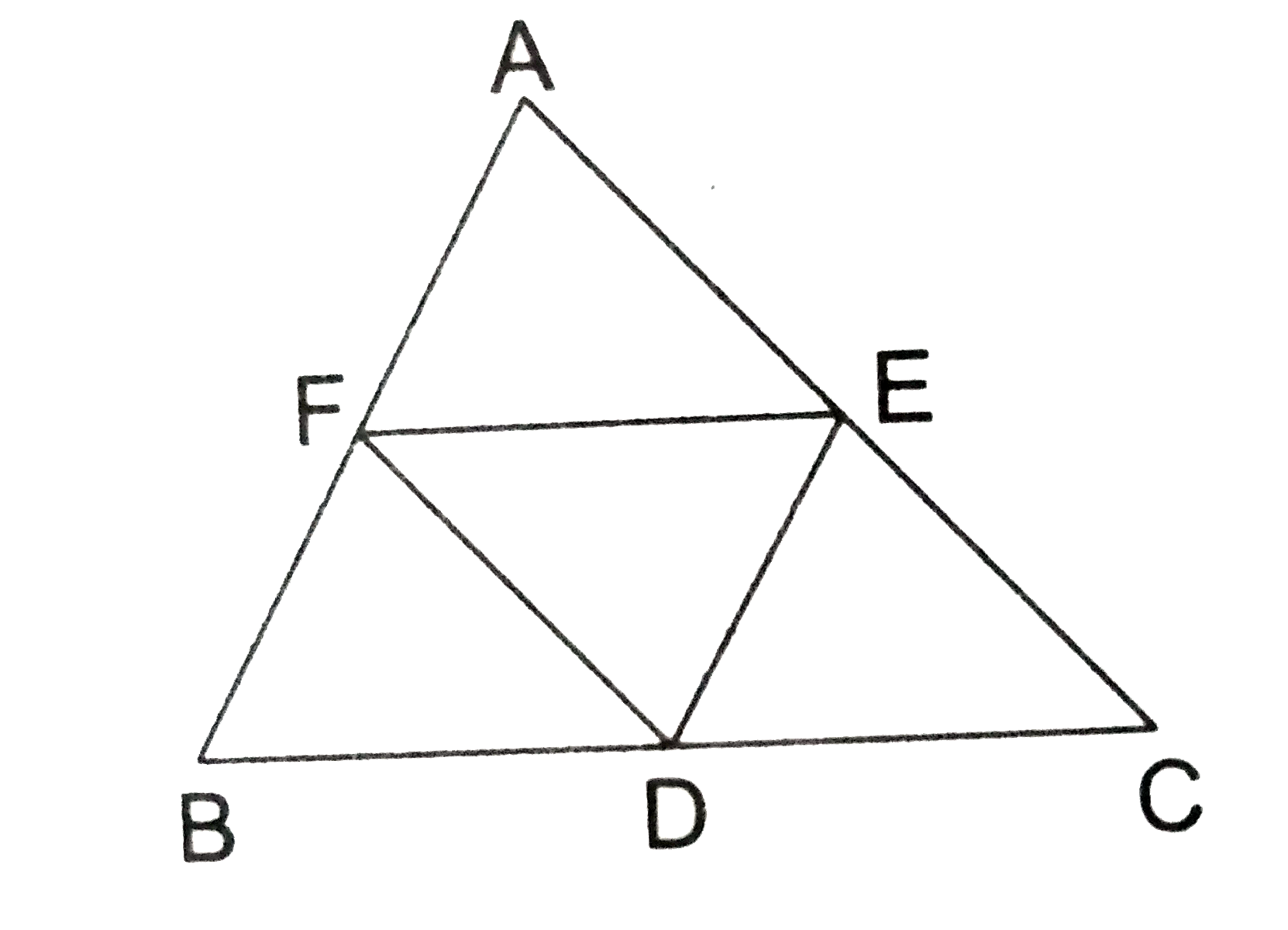
D,E और F क्रमशः त्रिभुज ABC की भुजाओं BC ,CA और AB के मध्य बिंदु है| दर्शाइए की ltBrgt BDEF एक समांतर चतुर्भुज है |
(ii) ar(DEF)=14ar(ABC)
ar(BDEF)=12ar(ABC)
∵F,AB का और E,AC का मध्य बिंदु है
∴EF∣∣BC और EF=12BC=BD
इसी प्रकार DE∣∣AB और DE=12AB=BF
अतः BDEF एक समांतर चतुर्भुज है|
अतः (i ) सिद्ध हो गया|
(ii) इसी प्रकार यह साबित किया जा सकता है की FDCE तथा क्षेत्र AFDE में से प्रत्येक एक समांतर चतुर्भुज है|
अब BDEF एक समांतर चतुर्भुज है और इसका विकर्ण समांतर चतुर्भुज को बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करता है|
∴ar(ΔBDF)=ar(ΔDEF) ...(i)
उसी प्रकार समांतर चतुर्भुज FDCE में ar(ΔEDC)=ar(ΔDEF) ...(ii)
तथा समांतर चतुर्भुज AFDE में ar(ΔAFE)=ar(ΔDEF) ...(iii)
अब समीकरण (i ) ,(ii ) और (iii ) से,
ar(ΔAFE)=ar(ΔDEF)=ar(ΔBDF)=ar(ΔEDC)
लेकिन ar(ΔAFE)+ar(ΔDEF)+ar(ΔBDF)+ar(EDC)=ar(ABC)
∴ 4[ar(ΔDEF)]=ar(ΔABC)
∴ ar(ΔDEF)=14ar(ΔABC)
(iii) ar (समांतर चतुर्भुज BDEF ) ar=(ΔDEF)+ar(ΔFEB)
=2ar(ΔDEF)=2⋅14ar(ΔABC)
=12ar(ΔABC)
(##KCS_HIN_MAT_IX_C11_SLV_006_S01.png" width="80%">
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:KC SINHAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 11.1
Explore 24 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:KC SINHAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:वस्तुनिष्ट प्रश्न
Explore 7 Videos
- समांतर चतुर्भुजBook:KC SINHAChapter:समांतर चतुर्भुजExercise:वस्तुनिष्ठ प्रश्न
Explore 9 Videos
- हीरोन का सूत्र Book:KC SINHAChapter:हीरोन का सूत्र Exercise:वस्तुनिष्ठ प्रश्न
Explore 13 Videos
Similar Questions
रिक्त स्थान को भरें :
(i) सर्वांगसम आयतों के क्षेत्रफल ...........होते है|
(ii) किसी समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का .....होता है
(iii) समलम्ब का क्षेत्रफल उसके समांतर भुजाओं के बीच की दुरी तथा समांतर भुजाओं के योग के गुणनफल का ......होता है|
(iv) सर्वांगसम त्रिभुजों के क्षेत्रफल ........होते है|
(v) एक ही आधार तथा एक ही समांतर रेखाओं के मध्य बने त्रिभुज क्षेत्रफल में ...........होते है|
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
View Solutionयदि किसी ΔABC में BC=a,CA=b AB=c हो तो ΔABC की अर्धपरिमिति है
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
View Solutionत्रिभुज ABC की भुजाओं BC , CA तथा AB के मध्य-बिंदु क्रमशा D , E तथा F है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है जिसका क्षेत्रफल ΔABC का आधा है। साथ ही, सिद्ध कीजिए कि ar(ΔDEF)=14ar(ΔABC) तथा ar(।।gmBDEF)=12ar(ΔABC)
View Solutionयदि दो त्रिभुज ABC और DEF इस प्रकार है कि ABDE=BCEF=CAFD=25 तो ar(ΔABC):ar(ΔDEF)=
View SolutionD, E और F क्रमशः त्रिभुज ABC की भुजाओं BC, CA और AB के मध्य-बिन्दु है। दर्शाइए कि :
(i) BDEF का समान्तर चतुर्भुज है।
(ii) ar(DEF)=14ar(ABC)
(iii) ar(BDEF)=12ar(ABC)
View SolutionD, E तथा F, ΔABC कि क्रमश : भुजाओ BC, CA तथा AB के मध्यबिंदु है। सिद्ध कीजिए कि BDEF एक समांतर चतुर्भुज है तथा इसका क्षेत्रफल ΔABC के क्षेत्रफल का आधा है।
यह भी दिखाइए कि ar(DEF)=14ar(ABC).
View SolutionD,E and F are respectively the mid-points of the sides BC, CA and AB of △ABC show that
(i) BDEF is a parallelogram.
(ii) ar (DEF) = 14 ar (ABC)
(iii) ar(BDEF)=12 ar (ABC)
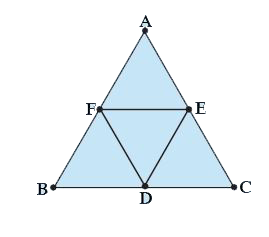
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
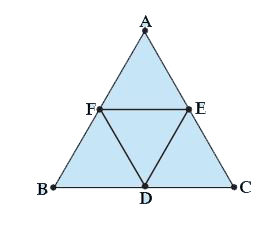
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
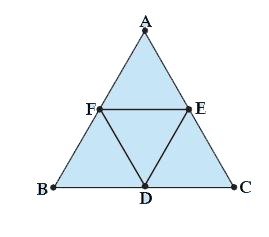
View SolutionIn the figure, ΔABC, D, E, F are the midpoints of sides BC, CA and AB respectively. Show that
(i) BDEF is a parallelogram
(ii) ar(ΔDEF)=14ar(ΔABC)
(iii) ar(BDEF)=12ar(ΔABC)
View SolutionD, E and F are the midpoints of triangles ABC BC, CA and AB respectively. ar (DEF) =1/4 ar (ABC)
View SolutionD, E ਅਤੇ F ਕ੍ਰਮਵਾਰ ਤ੍ਰਿਭੁਜ ABC ਦੀਆਂ ਭੁਜਾਵਾਂ BC,CA ਅਤੇ AB ਦੇ ਮੱਧ-ਬਿੰਦੂ ਹਨ।ਦਰਸਾਉ ਕਿ:- ar(BDEF)=12ar(ABC)
View SolutionIn triangle ABC ,P is a point on BC such that BP : PC = 1 : 2 and Q is the mid point of BP. then, ar(triangle ABQ) :ar (triangle ABC) is equal to: त्रिभुज ABC में, P, BC पर स्थित ऐसा बिंदु है कि BP : PC = 1 : 2 है और Q, BP का मध्य बिंदु है | तो ar(triangle ABQ) :ar (triangle ABC) का मान क्या होगा ?
View Solution
