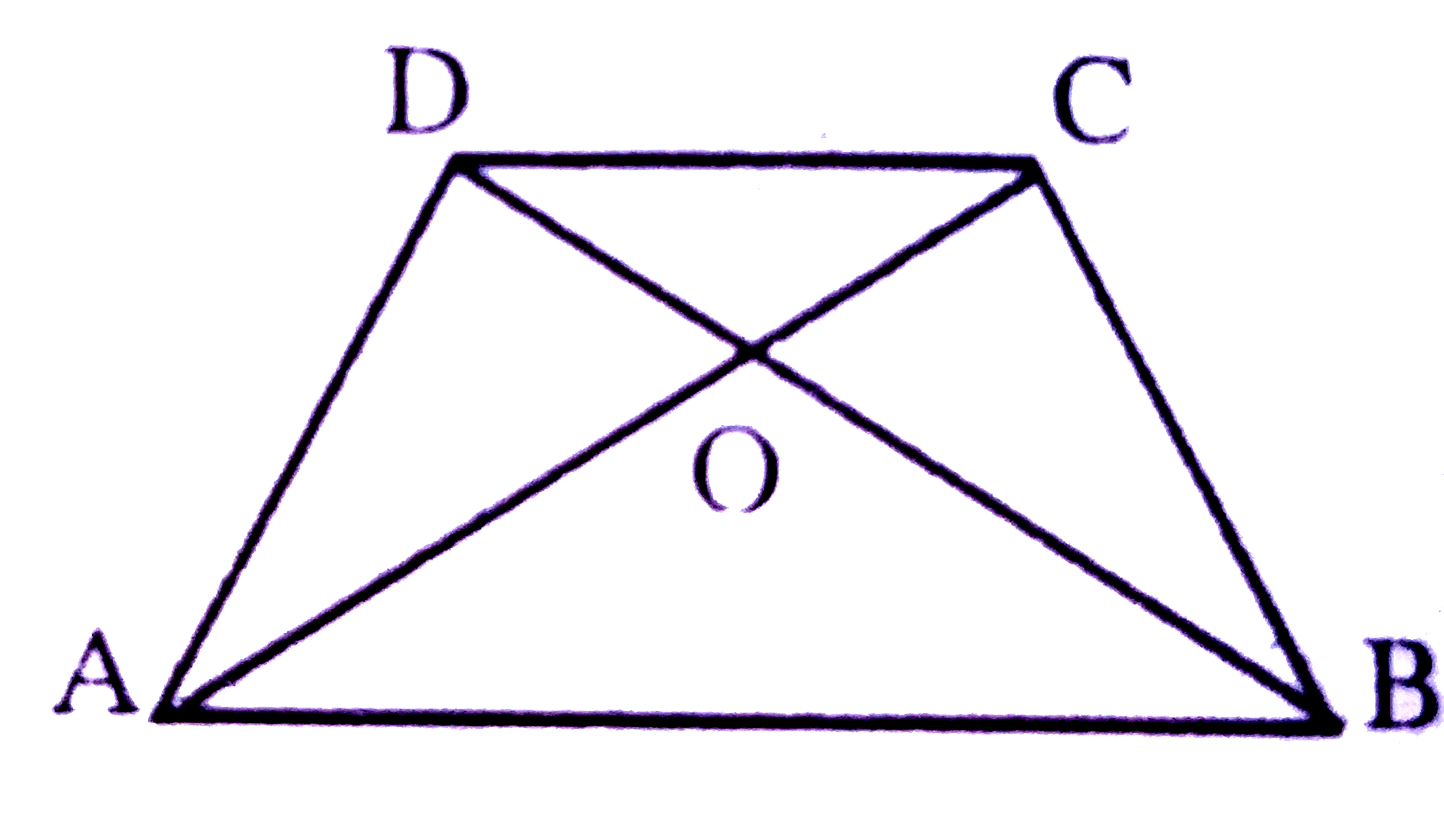
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते है की
है| सिद्ध कीजिए की ABCD एक समलम्ब है|
ABCD एक चतुर्भुज है जिसके विकर्ण AC तथा BD ,O बिंदु पर काटते है|
प्रमाण : यहाँ
दोंनो तरफ जोड़ देने से ltBrgt जोड़ने से हमे मिलता है
ltBrgt या
या
अब और एक ही आधार AB पर स्थित है तथा ltBrgt ltBrgt अतः और की ऊंचाई बराबर है अर्थात वे दोनों एक ही समांतर रेखाओं के बीच स्थित है ltBrgt
अतः ABCD एक समलम्ब चतुर्भुज है|
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:KC SINHAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 11.1
Explore 24 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:KC SINHAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:वस्तुनिष्ट प्रश्न
Explore 7 Videos
- समांतर चतुर्भुजBook:KC SINHAChapter:समांतर चतुर्भुजExercise:वस्तुनिष्ठ प्रश्न
Explore 9 Videos
- हीरोन का सूत्र Book:KC SINHAChapter:हीरोन का सूत्र Exercise:वस्तुनिष्ठ प्रश्न
Explore 13 Videos
Similar Questions
रिक्त स्थान को भरें :
(i) सर्वांगसम आयतों के क्षेत्रफल ...........होते है|
(ii) किसी समचतुर्भुज का क्षेत्रफल उसके विकर्णों की लम्बाइयों के गुणनफल का .....होता है
(iii) समलम्ब का क्षेत्रफल उसके समांतर भुजाओं के बीच की दुरी तथा समांतर भुजाओं के योग के गुणनफल का ......होता है|
(iv) सर्वांगसम त्रिभुजों के क्षेत्रफल ........होते है|
(v) एक ही आधार तथा एक ही समांतर रेखाओं के मध्य बने त्रिभुज क्षेत्रफल में ...........होते है|
View Solutionसमचतुर्भुज के विकर्णों का गुणनफल समचतुर्भुज के क्षेत्रफल का कितना गुना होता है ?
View Solutionचतुर्भुज के चारों कोणों का योग कितना समकोण होता है?
View Solutionयदि किसी ΔABC में BC=a,CA=b AB=c हो तो ΔABC की अर्धपरिमिति है
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a trapezium ABCD with ABCD intersect each where at O. Prove that ar (AOD)=ar(BOC).
View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View Solutionएक समलंब ABCD , जिसमें AB ।। DC है , के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते है । दर्शाइए कि ar(AOD)=ar(BOC) है
View Solutionचतुर्भुज ACBD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते है कि ar(AOD)=ar(BOC) है सिद्ध कीजिए कि ABCD एक समलंब है
View Solutionएक समलम्ब ABCD जिससे AB∣∣DC है के विकर्ण AC और BD परस्पर O प्रतिछेद करते है |दर्शाइए की ar(AOD)=ar(BOC) है|
View Solutionएक चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि ar(AOD) = ar(BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब है।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View SolutionDiagonals AC and BD of a trapezium ABCD with AB∣∣DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
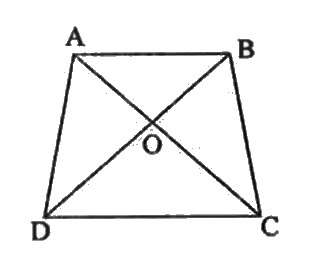
View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC interseet each other ar at O. Prove that ar (AOD) = BOC.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC) . Prove that ABCD is a trapezium.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
View Solution
