निम्नलिखित रैखिक समीकरण युग्मों में कौन संगत/असंगत है ? यहदि संगत है तब उनके हल आलेखीय विधि से ज्ञात करें।
(i) x+y=52x+2y=10 (ii) 2x+y−6=02x−2y−4=0 (iii) 2x−2y−2=04x−4y−5=0 (iv) x−y=83x−3y=16
(i)दत्त समीकरण है: x+y=5………….i
और 2x+2y=10………..ii
यहां a1=1,b1=1,c1=5
a2=2,b2=2,c2=10
अब a1a2=12,c1c2=510=12 चूंकि a1a2=b1b2=c1c2
अतः दत्त समीकरणों द्वारा निरूपित रेखायें संपाती है और इसलिए दत्त समीकरण निकाय संगत है और उसका अनन्ततः अनेक हल हैं।
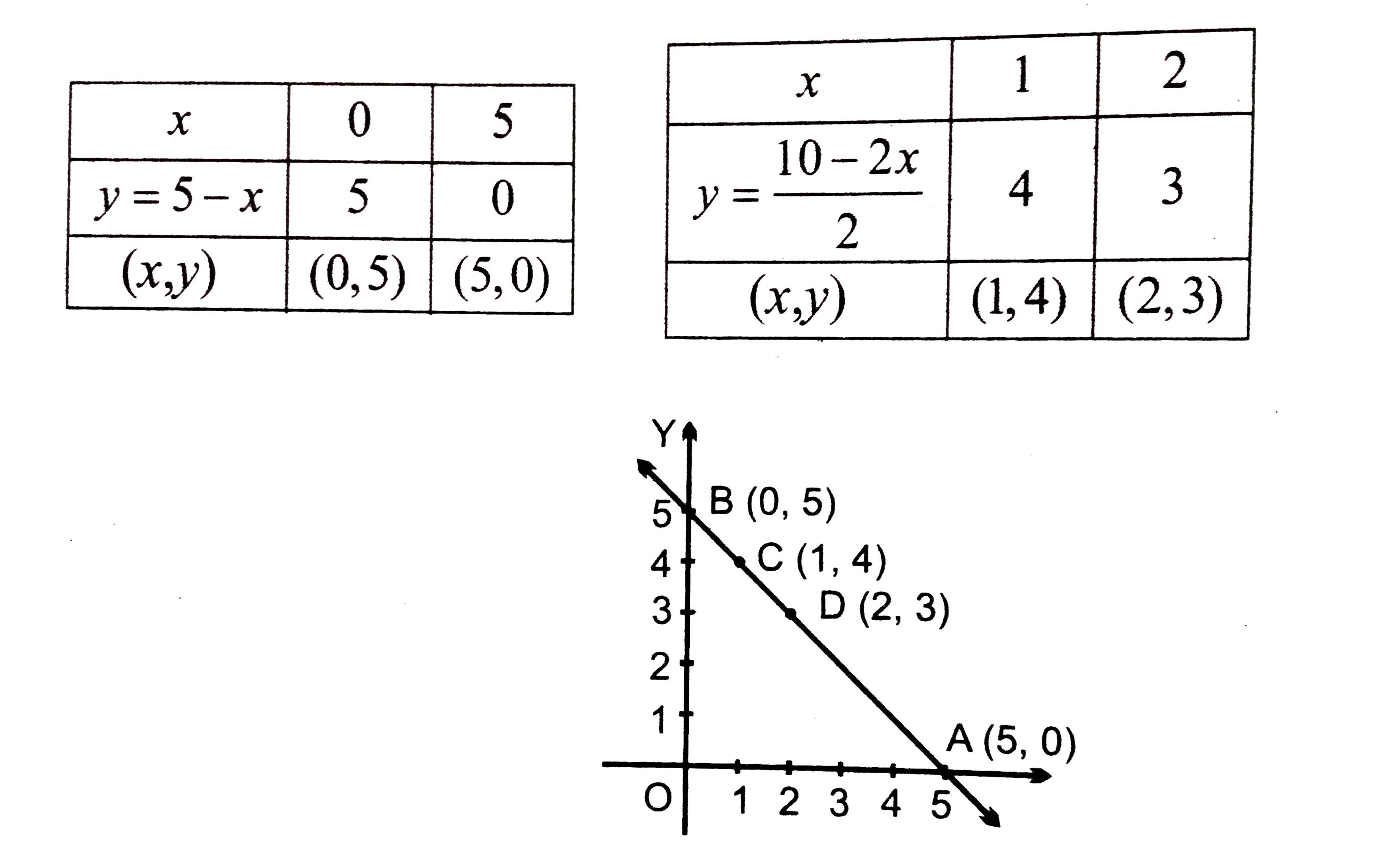
मान लें A≡(0,5),B≡(5,0),C≡(1,4),D≡(2,3)
समीकरण (i) और (ii) को निरूपित करनेवाली रेखाओं के आलेख AB और CD है जो संपाती है।
संपाती रेखा पर स्थित प्रतयेक बिंदु के नियामक एक हल होगा।
(ii) दत्त समीकरण है 2x+y=6……………iii
और 4x−2y=4…….iv
यहां a1=2,b1=1,c1=6
a2=4,b2=−2,c2=4
अब a1a2=24=12,b1b2=1−2=−12,c1c2=64=32
चूंकि a1a2≠b1b2 अतः दत्त रैखिक समीकरण युग्म संगत है और इसका अद्वितीय हल है।
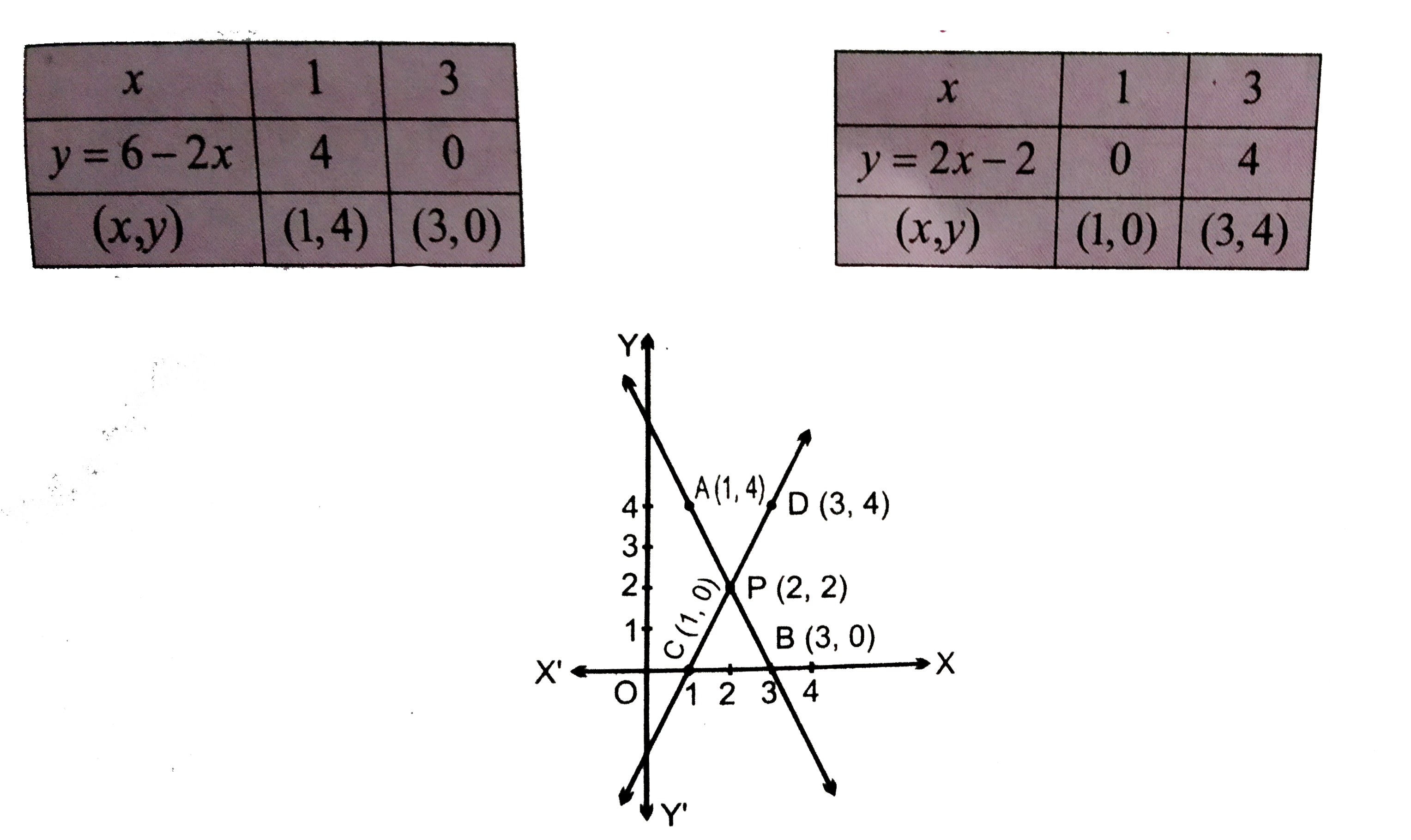
समीकरण (iii) और (iv) को निरूपित करनेवाली रेखाओं के आलेख AB और CD है। ये रेखायें बिंदु P(2,2) पर मिलती है।
अतः दत्त समीकरण युग्म के हल हैं :x=2,y=2
(iii) दत्त समीकरण है 2x−2y=2……….v
और 4x−4y=5 …………..vi
यहां a1=2,b1=−2,c1=2
a2=4,b2−4,c2=5
अब a1a2=24=12,b1b2=−2−4=12,c1c2=25
चूंकि a1a2=b1b2≠c1c2 अतः दत्त समीकरण युग्म असंगत है अर्थात इसका कोई हल नहीं है।
(iv) दत्त समीकरण है x−y=8…………..vii
और 3x−3y=16………..viii
यहां a1=1,b1=−1,c1=8
a2=3,b2=−3,c2=16
अब a1a2=13,b1b2=−1−3=13,c1c2=816=12
चूंकि a1a2=b1b2≠c1c2 अतः दत्त समीकरण युग्म असंगत है अर्थात इसका कोई हल नहीं है।
Topper's Solved these Questions
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - 3.1 दीर्घ उत्तरीय प्रश्न
27 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - 3.1 लघु उत्तरीय प्रश्न
2 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - वस्तुनिष्ठ प्रश्न
28 Videos
- द्विघात समीकरण BOOK - KC SINHACHAPTER - द्विघात समीकरण EXERCISE - वस्तुनिष्ट प्रशन
37 Videos
Similar Questions
सुधा अपने सखियों के साथ बाजार गई। वे गोकलगप्पा और दहीबड़ा खाना चाहती थी। उनके द्वारा ली गई गोलगप्पा की प्लेटों की संख्या, दहीबड़ा की प्लेटों की संख्या की आधी है। गोलगप्पा के एक प्लेट की कीमत 10रू0 तथा दहीबड़ा के एक प्लेट की कीमत 5रू0 थे, उसने 60 रू0 खर्च किए। इस स्थिति (कथन) का बीजीय तथा आलेखीय निरूपण करें।
View Solutionजांच करें कि x और y के कौन मान युग्म समीकरण 4x+3y+24=0 के हल है?
(i) x=0,y=8 (ii) x=−6,y=0 (iii) x=1,y=−2
(iv)x=−3,y=4 (v) x=1,y=−2 (vi) x=−4,y=2
View SolutionΔABC में DE∣∣BC और ADDB=53 तब AEAC=
View Solutionयदि a और b समीकरण x2−ax+b=0 के मूल है तब
View SolutionWhich of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i) x + y = 5, 2x + 2y = 10
(ii) x - y = 8, 3x - 3y =16
(iii) 2x + y - 6 = 0, 4x - 2y - 4 = 0
(iv) 2x - 2y - 2 = 0, 4x - 4y - 5 = 0
View Solutionsolve: (2) / (2x + y) - (1) / (x-2y) + (5) / (9) = 0 and (9) / (2x + y) - (6) / (x-2y ) + 4 = 0
View SolutionThe lines x+2y+3=0,x+2y−7=0,and2x−y−4=0 are the sides of a square. The equation of the remaining side of the square can be (a) 2x−y+6=0 (b) 2x−y+8=0 (c) 2x−y−10=0 (d) 2x−y−14=0
View SolutionEquation of the diameter of the circle x^(2)+y^(2)-2x+4y=0 which passes through the origin is x+2y=0 b.x-2y=0 c.2x+y=0 d.2x-y=0
View SolutionFind the intercepts cuts on X-axis and Y -axis from the following lines :
(i)3x+4y=12 (ii)2x−5y=8
(iii)x+2y+3=0 (iv)2x−y+3=0
View Solutionनिम्न रैखिक समीकरणों के युग्मों में से कौन -से युग्म संगत/असंगत है , यदि संगत है तो ग्राफिय विधि से हल कीजिए :
(i) x+y=5,2x+2y=10
(ii) x−y=8,3x−3y=16
(iii) 2x+y−6=0,4x−2y−4=0
(iv) 2x−2y−2=0,4x−4y−5=0
View SolutionThe line 3x + 2y = 6 will divide the quadrilateral formed y the lines x + y = 5, y – 2x = 8, 3y + 2x = 0 & 4y – x = 0 in
View Solutionरेखाओ x = 0, y = 0, 2x + 3y = 5 से बने त्रिभुज के परिवृत का समीकरण है
View Solutionनिम्नलिखित समीकरण युग्मों को एवं के मान के लिए हल करें|
x+2y+1=0
2x−3y−12=0
View Solutionx = 2, y = -1 निम्न में से कौन - कौन सा रैखिक समीकरण का हल हैं।
(i) x+2y=0
(ii) x+2y=4
(iii) 2x+y=0
(iv) 2x+y=3
View SolutionWhich of the following pairs of linear equations are consistent / inconsistent? If consistent, obtain the solution graphically :(i) x+y=5, 2x+2y=10(ii) xy=8, 3x3y=16(iii) 2x+y6=0, 4x2y−4=0
View Solution
