सिध्द करे कि किसी त्रिभुज का क्षेत्रफल इसकी भुजाओ के मध्य बिन्दुऔ से बने त्रिभुज के क्षेत्रफल का चार गुण
माना कि ABC एक त्रिभुज है |
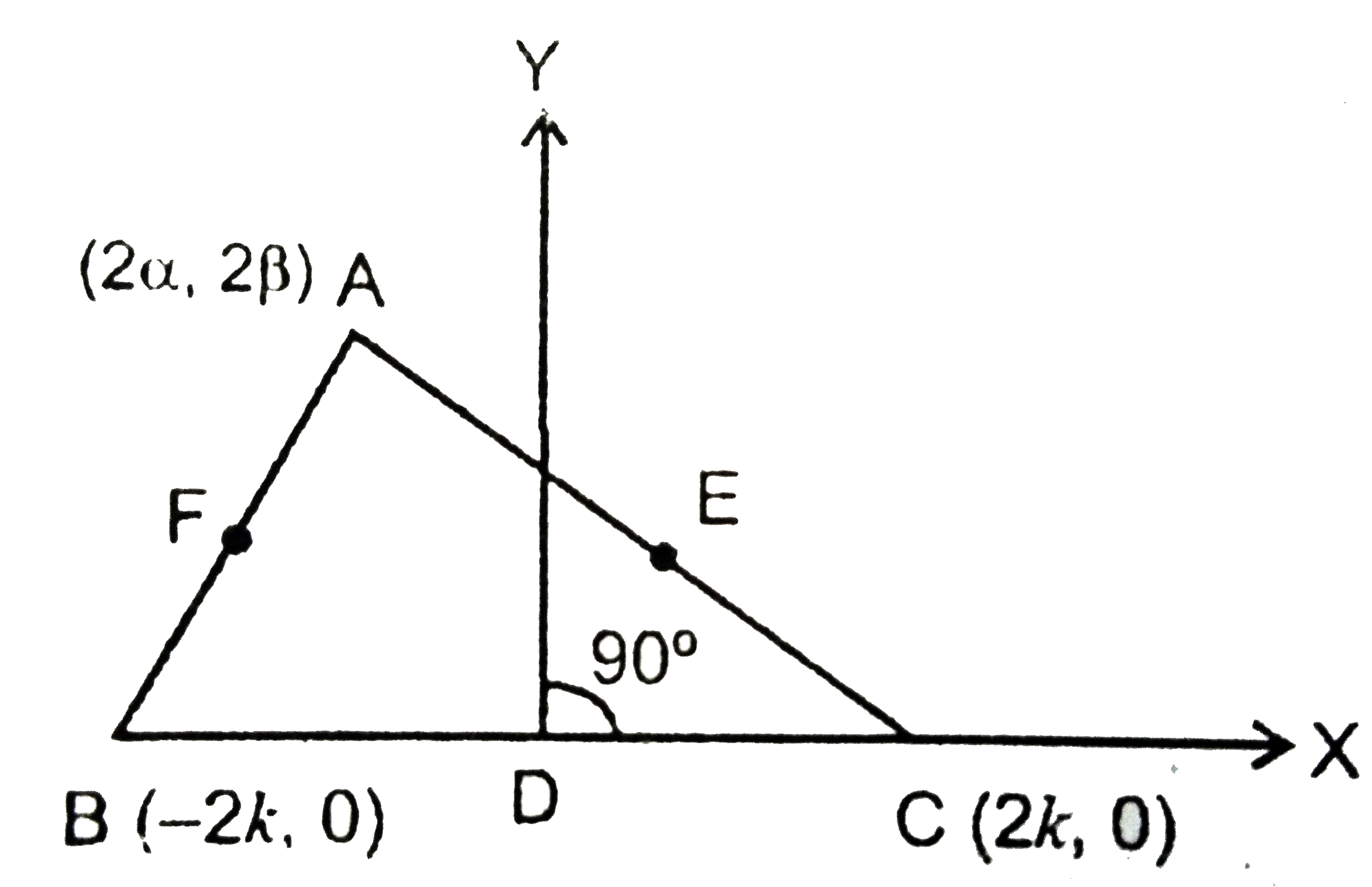
माना कि D,BC का मध्य बिन्दु है तथा BC = 4k D मूल बिन्दु तथा DC को x -अक्ष माना |
तब B≡(−2k,0),C≡(2k,0)
माना कि A≡(2α,2β)
माना कि E और F क्रमश : AC और AB के मध्य बिन्दु है |
अब ΔABC का क्षेत्रफल =∣∣∣12[2α(0−0)−2k(0−2β)+2k(2β−0)]∣∣∣
=12|8kβ|=4|kβ|
पुन :D(0,0)E≡(α+k,β),F≡(αk,β)
अतः ΔDEF का क्षेत्रफल =∣12[0(β−β)+(α+k)(β−0)+(α−k)(0−β))]∣∣∣
(i) और (ii) से स्पष्ट है कि ΔABC का क्षेत्रफल = 4×ΔDEF का क्षेत्रफल
Topper's Solved these Questions
- निर्देशांक ज्यामिति Book:KC SINHAChapter:निर्देशांक ज्यामिति Exercise:प्रश्नावली 7.1 (अतिलघु उत्तरीय प्रश्न )
Explore 13 Videos
- निर्देशांक ज्यामिति Book:KC SINHAChapter:निर्देशांक ज्यामिति Exercise:प्रश्नावली 7.1 (लघु उत्तरीय प्रश्न )
Explore 5 Videos
- द्विघात समीकरण Book:KC SINHAChapter:द्विघात समीकरण Exercise:वस्तुनिष्ट प्रशन
Explore 37 Videos
- पृष्ठीय क्षेत्रफल और आयतन Book:KC SINHAChapter:पृष्ठीय क्षेत्रफल और आयतन Exercise:वस्तुनिष्ट प्रश्न(Objective Questions)
Explore 30 Videos
Similar Questions
निम्नलिखित बिन्दुए किस चतुर्थेाश में स्थित है |
(10,−3)
View Solutionयदि किसी आयत के तीन शीर्ष (−2,0),(2,0),(2,1) है तो चौथे शीर्ष के नियामक ज्ञात कीजिए |
View Solutionयदि a और b समीकरण x2−ax+b=0 के मूल है तब
View Solutionएक खोखला धातुई गोला जिसकी बाह्य त्रिज्या 6cm और अन्तः त्रिज्या 4cm है को पिघलाया जाता है और इसे एक शंकु जिसके आधार की त्रिज्या 6cm है, के रूप में ढाला जाता है, तो शंकु की ऊँचाई है:
View Solutionकिसी त्रिभुज कि भुजाओ के मध्य बिन्दुओ के निर्देशांक क्रमशः (2,1),(−5,7) तथा (−5,5) है त्रिभुज कि भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionत्रिभुज का क्षेत्रफल | उदाहरण
View Solutionसारणिक के अनुप्रयोग | त्रिभुज का क्षेत्रफल | उदाहरण
View Solutionत्रिभुज का क्षेत्रफल | उदाहरण
View Solutionहीरोन के सूत्र के प्रयोग से किसी त्रिभुज का क्षेत्रफल ज्ञात करना
View SolutionRevision|त्रिभुज का क्षेत्रफल#!#हीरोन के सूत्र द्वारा#!#महत्वपूर्ण प्रश्न
View SolutionRevision|हीरोन के सूत्र पर आधारित महत्वपूर्ण प्रश्न#!#त्रिभुज का क्षेत्रफल तथा चतुर्भुज का क्षेत्रफल
View SolutionRevision |त्रिभुज का क्षेत्रफल #!#बिंदुओं के संरेख होने का प्रतिबंध
View SolutionRevision|त्रिभुज का क्षेत्रफल
View Solutionत्रिभुज का क्षेत्रफल
View Solutionभूमिका |त्रिभुज का क्षेत्रफल |समबाहु त्रिभुज का क्षेत्रफल |समद्विबाहु त्रिभुज का क्षेत्रफल |सारांश
View Solutionत्रिभुज का क्षेत्रफल |समबाहु त्रिभुज का क्षेत्रफल |समद्विबाहु त्रिभुज का क्षेत्रफल |हीरोन का सूत्र |उदाहरण|सारांश
View Solution