(i) यदि cosθ=q√p2+q2,तो सिद्ध करें कि (√p2+q2p+qp)2=√p2+q2+q√p2+q2−q
R.H.S. =1+q√p2+q21−q√p2+q2=1+cosθ1−cosθ[अंश और हर को √p2+q2 से भाग देने पर ]
=1+cosθ1−cosθ×1+cosθ1+cosθ=(1−cosθ)21−cos2θ=(1+cosθ)2sin2θ
=(1+cosθsinθ)2=(1sinθ+cosθsinθ)2=(cosecθ+cotθ)2 ....(i)
∵cosθ=q√p2+q2=bh
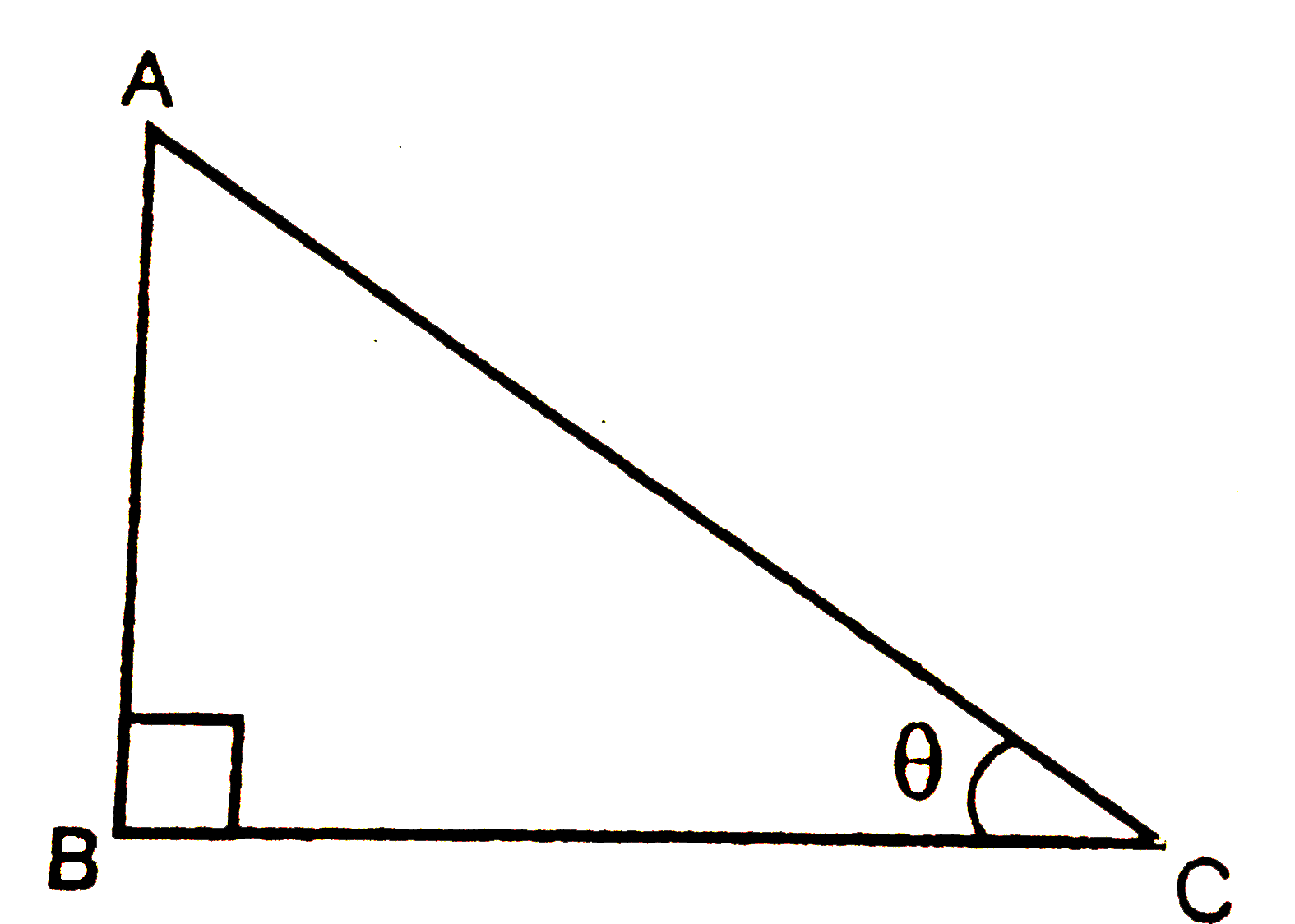
हम समकोण त्रिभुज ABC खींचते है , जिसमें
∠ACB=θ,BC=q,AC=√p2+q2
अब AB=√AC2−BC2=√(√p2+q2)2−q2=√p2+q2−q2=p
∴cosecθ=hp=ACAB=√p2+q2p और cotθ=bp=qp
समीo (i) R.H.S. = (√p2+q2p+qp) = L.H.S.]
Topper's Solved these Questions
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - लघु उत्तरीय प्रश्न
87 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - वस्तुनिष्ठ प्रश्न
3 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- त्रिकोणमिति के कुछ अनुप्रयोग BOOK - KC SINHACHAPTER - त्रिकोणमिति के कुछ अनुप्रयोग EXERCISE - वस्तुनिष्ठ प्रश्न
14 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - वस्तुनिष्ठ प्रश्न
28 Videos
Similar Questions
यदि tanA=ba,जहाँ a और b वास्तविक संख्याएँ है , तो sin2A का मान ज्ञात करें ।
View Solutionयदि tanθ=512, तब निम्नलिखित में sinθ का मान कौन है ?
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि एक मीनार के पाद से 100 m दूर स्थित बिंदु पर मीनार का उन्नयन कोण60∘ है , तो मीनार कि ऊँचाई है :
View SolutionΔABC में DE∣∣BC और ADDB=53 तब AEAC=
View Solutionif x=(sqrt(p^(2)+q^(2))+sqrt(p^(2)-q^(2)))/(sqrt(p^(2)+q^(2))-sqrt(p^(2)-q^(2))), then q^(2)x^(2)-2p^(2)x+q^(2)=?
View SolutionIf x=(sqrt(p^(6)+q^(2))+sqrt(p^(2)-q^(2)))/(sqrt(p^(2)+q^(2))-sqrt(p^(2)-q^(2))) then q^(2)x^(2)-2p^(2)x+q^(2)=?
View SolutionIf x=√p+q+√p−q√p+q−√p−q find the value of qx2−2px+q
View Solutionlim_(x rarr0)(sqrt(4^(2)+p^(2))-p)/(sqrt(x^(2)-q^(2)-q))
View SolutionAT what angle two forces (P +Q) and (P-Q) act so that resultant is (i) sqrt(2 P^2 + Q^2) (ii) sqrt(2 P^2 + Q^2) (iii) sqrt(2 P^2 + Q^2) .
View Solutionयदि qcosθ=√q2−p2,तो सिद्ध करें कि qsinθ=p
View Solutionif : p⋅cosθ=√p2+q2.sinθ,then:q⋅sinθ=
View SolutionIf the ratio of A.M. of two numbers x and y to their G.M. is p : q, show that,
x:y=(p+√p2−q2):(p−√p2−q2)
View Solutionlimx→0√x2+q2−q√x2+p2−p
View SolutionLet θ=π24 and 1tan2θ−tan2θ=√p+√q(p>q)p,q∈N then the value of √p−q is
View Solution
