10 cm त्रिज्या वाले एक शंकु को उसके अक्ष के मध्य बिन्दु से आधार के समान्तर एक तल खींचकर दो भागों से बाँटा जाता है। दोनों भागों के आयतनों कि तुनला करें। |
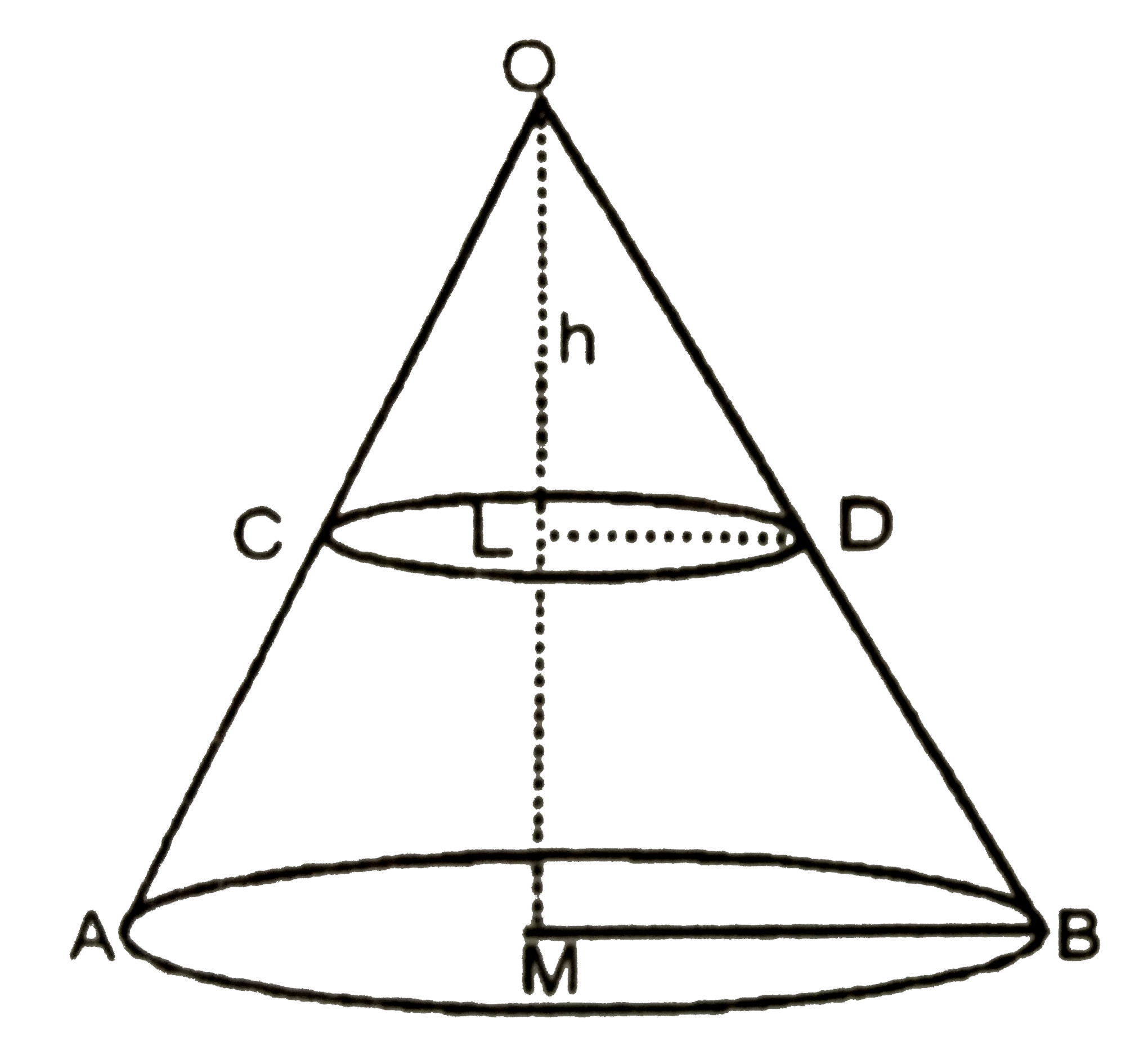
माना कि OAB एक शंकु है और OM इसका अक्ष है और माना कि L, OM का मध्य बिन्दु है |
माना कि OM=h cm
तब OL=LM=h2 cm और MB=10 cm
अब, ΔOLD~ΔOMB
∴ OLOM=LDMB ⇒ (h/2)h=LD10 cm
⇒ LD=5 cm
तल CD, शंकु को दो भागों में बाँटती है,
यथा (i) 5 cm त्रिज्या और h/2 cm ऊँचाई वाला एक लघुतर शंकु,
(ii) शंकु के छिन्नक लिए :
छिन्नक के ऊपरी सिरे की त्रिज्या r = 5 cm
निचले सिरे की त्रिज्या R = 10 cm
छिन्नक की ऊँचाई =h2 cm
छोटे शंकु का आयतन =(13×π×5×h2) cm3=(25πh6) cm3
शंकु के छिन्नक का आयतन =13×πh2.[(10)2+(5)2+10×5]cm3=(175πh6) cm3
अभीष्ट आयतनों का अनुपात =25πh6:175πh6=25:175=1:7.
Topper's Solved these Questions
- पृष्ठीय क्षेत्रफल और आयतन BOOK - KC SINHACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - 13.1
7 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - KC SINHACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - 13.2
18 Videos
- निर्देशांक ज्यामिति BOOK - KC SINHACHAPTER - निर्देशांक ज्यामिति EXERCISE - वस्तुनिष्ठ प्रश्न
36 Videos
- प्रायिकता या सम्भावितBOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - वस्तुनिष्ठ प्रश्न
54 Videos
Similar Questions
8cm भुजा वाले दो घन बराबर से जोड़ दिए गए है। परिणामी धनाभ के पृष्ट क्षेत्रफल एवं आयतन ज्ञात करे।
View Solutionएक शंक्वाकार खिलौना, 7 cm व्यास बाले अर्द्धगोले पर अध्यारोंपित है। खिलौने की कुल ऊँचाई 14.5 cm है । खिलोने का आयतन ज्ञात करे। [π=227 मान लें]
View Solutionबिन्दु (−3,−5) किस चतुर्थेाश में स्थित है |
View Solutionदो सिक्के उछालने में दो पट आने के प्रायिकता है:
View Solutionएक नली में 12 सेमी.3/से. कि दर से बालू उंडेली जा रही है। उंडेली गई बालू से एक शंकु का निर्माण इस प्रकार होता है कि शंकु कि ऊंचाई सदैव आधार कि त्रिज्या का 16 वा भाग होती ह। बालू के शंकु कि ऊंचाई में किस गति से वृद्धि हो रही है जबकि ऊंचाई 4 सेमी. है ?
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solution1 से 11 तक के पूर्णांकों में से यादृच्छया दो पूर्णांकों को चुना गया है | दोनों पूर्णांकों के विषय होने कि प्रायिकता ज्ञात करो यदि यह ज्ञात है कि दोनों पूर्णांकों का योग सम है |
View SolutionY-अक्ष के समान्तर तथा समतलों x+y+z=1 और 2x+3y−z+4=0 के प्रतिच्छेदन से होकर जाने वाला समतल निम्न में से किस बिन्दु से भी होकर जाता है ?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionवृक्क नलिका के विभिन्न भागों के कार्य
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solutionएक बिन्दु की रेखा से लम्बवत दूरी |दो समांतर रेखाओ के मध्य दूरी
View Solutionकिसी ठोस के विभिन्न भागों से देखना
View Solutionदो रेखाओ के मध्य कोण |बिन्दु से रेखा पर लंब
View Solution
