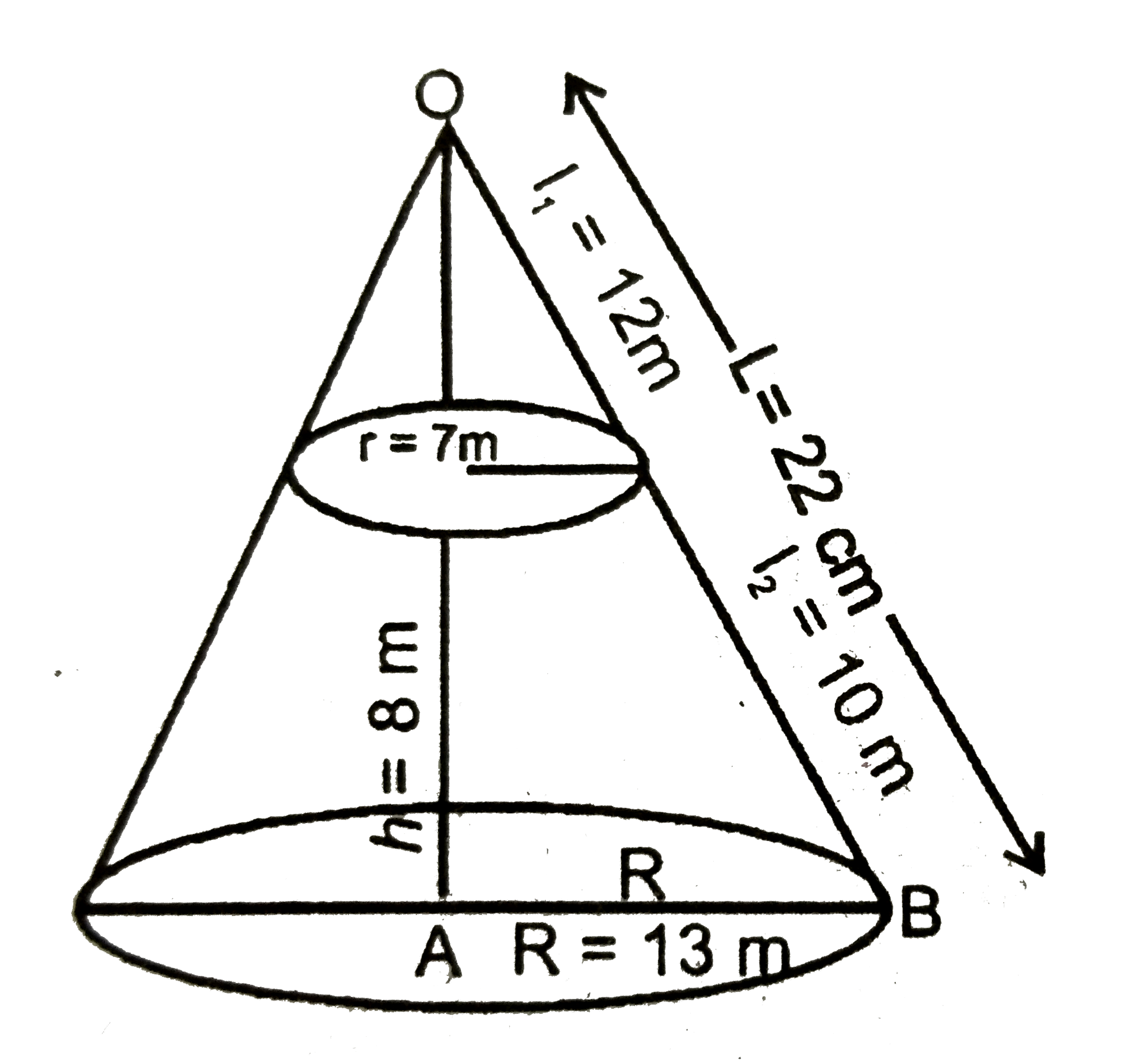
एक टेन्ट, एक शंकु के छिन्नक के आकार का है जिसका ऊपरी सिरा शंक्वाकार है। छिन्नक के आधार एवं शीर्ष के व्यास क्रमश : 14 m एवं 26 m हैं। यदि टेन्ट के छिन्नक की ऊंचाई 8 m और शंक्वाकार भाग की तिरछी ऊँचाई 12 m है, तो टेन्ट को बनाने का क्षेत्रफल ज्ञात कीजिए। (छिन्नक के ऊपरी सतह और शंकु के आधार की त्रिज्याओं को समान मानें)
शंकु के छिन्नक की ऊपरी त्रिज्या r=142=7 m
शंकु के छिन्नक की निचली त्रिज्या R=262=13 m
छिन्नक की ऊँचाई h = 8 m , शंकु की तिरछी ऊँचाई l1=12 m
शंकु के छिन्नक की तिरछी ऊँचाई
l2=√h2+(R−r)2=√(8)2+(13−7)2
=√64+36=√100=10 m
कैनवस का क्षेत्रफल = (शंकु के छिन्नक के वक्र सतह का क्षे०) + (ऊपरी शंकु के वक्र सतह का क्षे०)
= वृहत शंकु की वक्र सतह का क्षे० =πRL [R=13 mऔर L=l1+l2=12+10=22 m]
=227×13×22=62927=898.86 m2 (लगभग)
Topper's Solved these Questions
- पृष्ठीय क्षेत्रफल और आयतन BOOK - KC SINHACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - 13.1
7 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - KC SINHACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - 13.2
18 Videos
- निर्देशांक ज्यामिति BOOK - KC SINHACHAPTER - निर्देशांक ज्यामिति EXERCISE - वस्तुनिष्ठ प्रश्न
36 Videos
- प्रायिकता या सम्भावितBOOK - KC SINHACHAPTER - प्रायिकता या सम्भावितEXERCISE - वस्तुनिष्ठ प्रश्न
54 Videos
Similar Questions
8cm भुजा वाले दो घन बराबर से जोड़ दिए गए है। परिणामी धनाभ के पृष्ट क्षेत्रफल एवं आयतन ज्ञात करे।
View Solutionएक शंक्वाकार खिलौना, 7 cm व्यास बाले अर्द्धगोले पर अध्यारोंपित है। खिलौने की कुल ऊँचाई 14.5 cm है । खिलोने का आयतन ज्ञात करे। [π=227 मान लें]
View Solutionबिन्दु (−3,−5) किस चतुर्थेाश में स्थित है |
View Solutionदो सिक्के उछालने में दो पट आने के प्रायिकता है:
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionशंकु का छिन्नक | उदाहरण
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionयदि किसी वृत्त के व्यास का एक सिरा (3,4) और केन्द्र (2,3) हो, तो दूसरे सिरे के निर्देशांक ज्ञात कीजिए।
View SolutionBoards 2021|शंकु के छिन्नक को समझे#!#Revision
View Solutionशंकु का छिन्नक|छिन्नक का पृष्ठीय क्षेत्रफल एवं आयतन#!#उदाहरण
View Solutionशंकु का छिन्नक|पृष्ठीय क्षेत्रफल एवं आयतन#!#उदाहरण
View SolutionRevision#!#शंकु का छिन्नक
View SolutionThe radii of two circular faces of the frustum of a cone of height 21 cm are 3 cm and 2 cm respectively. What is the volume of the frustum of the cone in cubic cm? (Take π=227)
21 सेमी ऊंचाई वाले शंकु के छिन्नक के दो वृताकार फलकों की त्रिज्या क्रमशः 3 सेमी और 2 सेमी है। घन सेमी में शंकु के छिन्नक का आयतन कितना होगा ?
View SolutionThe volume of a right circular cone is equal to that of a sphere, whose radius is half the radius of the base of the cone. What is the ratio of the radius of the base to the height of the cone ?
एक लम्ब वृत्तीय शंकु का आयतन उस गोले के आयतन के बराबर है, जिसकी त्रिज्या शंकु के आधार की त्रिज्या से आधी है | शंकु के आधार की त्रिज्या और शंकु की ऊंचाई में क्या अनुपात है ?
View SolutionThe radii of two circular faces of frustum of a cone are 5 cm and 4 cm. If the height of the frustum is 21 cm, what is its volume in cubic cm? (Take π=227)
एक शंकु के छिन्नक के दो वृत्ताकर फलकों की त्रिज्या 5 सेमी और 4 सेमी है। यदि छिन्नक की ऊंचाई 21 सेमी है, तो घन सेमी में इसका आयतन कितना होगा ?
View Solution
