एक कलश (पात्र) में 25 गेंदे हैं, जिनमे से 10 गेंदों पर चिन्ह X अंकित हैं और शेष 15 पर चिन्ह Y अंकित हैं। कलश में से एक गेंद याद्रीच्या निकली जाती हैं और उस पर अंकित चिन्ह का नॉट (लिख) करके उसे कलश में प्रतिस्थापित कर दिया जाता हैं। यदि इस प्रकार से 6 गेंदे निकली जाती हों, तो निम्नलिखित प्रायिकताएँ ज्ञात कीजिये।
(i) सभी पर चिन्ह X अंकित हो।
(ii) 2 से अधिक पर चिन्ह Y नहीं अंकित होता।
(iii) कम से कम 1 गेंद पर चिन्ह Y अंकित हो।
(iv) X तथा Y चिन्हों से अंकित गेंदों कि संख्याएं समान हों।
X चिन्ह से अंकित गेंदों कि संख्या का माध्य भी ज्ञात कीजिये।
n=6 परिक्षण के लिए यह प्रयोग एक बरनॉली परिक्षण हैं। माना यहाँ चिन्ह X अंकित गेंदों का कलश में से निकलना सफलता हैं।
p=1025=25⇒q=1−25=35
∴ Z बंटन, n=6, p=25 तथा q=35 वाला एक द्विपद बंटन हैं।
∴P(Z=r)=(nCr).prqn−r=(6Cr)(25)&r(35)6−r
(i) P( सभी चिन्ह X अंकित वाले है) = P(6 सफलताएं)
=(6C6p6q0)=(25)6
(ii) P(2 से कम पर चिन्ह X अंकित न हो)
=P (न्यूनतम 4 सफलताएं)
=P(4)+P(5)+P(6)
=15×(25)4925+6×(25)5×35+1×(25)6×1
=(25)4[275+3625+425]=(25)4[135+36+425]
=(25)4×17525=7(25)4
(iii) P(कम-से-कम 1 गेंद पर चिन्ह 'Y' अंकित हो)
=P(न्यूनतम 1 न्यूनतम 1 असफलता)
=P(अधिकतम 5 सफलताएं)
=1−P(6)=1−(6C6)p6q0
=1−1×(25)6×1=1−(25)6
(iv) अभीष्ट प्रायिकता =P (तीन सफलताएं तथा तीन असफलताएं)
=P(3)=6C3p3q3=6C3(25)3(35)3
=20×(25)3×(35)3=20×8125×27125=8643125
अभीष्ट माध्य =np=6×25=2.4
Topper's Solved these Questions
- प्रायिकता BOOK - NOOTAN HINDICHAPTER - प्रायिकता EXERCISE - प्रशनावली 13.5
15 Videos
- प्रतिलोम त्रिकोणमितीय फलन BOOK - NOOTAN HINDICHAPTER - प्रतिलोम त्रिकोणमितीय फलन EXERCISE - विविध प्रश्नावली
17 Videos
- रैखिक प्रोग्रामन BOOK - NOOTAN HINDICHAPTER - रैखिक प्रोग्रामन EXERCISE - प्रश्नावली (विविध प्रश्नावली )
10 Videos
Similar Questions
एक पासे को 6 बार उछाला जाता है। यदि 'पासे पर सम संख्या प्राप्त होना' एक सफलता है तो निम्नलिखित की प्रायिकताएँ क्या होगी?
(i) तथ्यत: 5 सफलताएं?
(ii) न्यूनतम 5 सफलताएं?
(iii) अधिकतम 5 सफलताएं?
View Solutioncos−1(cos13π6)
View Solutionएक आहारविद दो भोज्यों P और Q का उपयोग करते हुए एक विशेष आहार तैयार करता है । भोज्य P का प्रत्येक पैकेट (जिसमे 30 ग्राम अंतव्रिष्ट है) में कैल्शियम के 6 मात्रक और विटामिन A के 6 मात्रक अंतव्रिष्ट हैं जबकि उसी मात्रक के भोज्य Q के पैकेट में कैल्शियम तत्व के 3 मात्रक, लौह-तत्व के 20 मात्रक, कोलेस्ट्रोल के 4 मात्रक और विटामिन A के 3 मात्रक अंतव्रिष्ट हैं । आहार में कम-से कम 240 मात्रक कैल्शियम, लौह-तत्व के कम-से-कम 460 मात्रक और कोलेस्ट्रोल के अधिक-से-अधिक 300 मात्रक अपेक्षित हैं । आहार में विटामिन A के मात्रा का अधिकतमीकरण करने के लिए प्रत्येक भोज्य के कितने पैकेटों का उपयोग होना चाहिए? आहार में विटामिन A की अधिकतम मात्रा क्या है?
View Solutionएक थैले में 10 गेंदे है जिनमे से प्रत्येक पर से तक के अंको में से अंक लिखा है। यदि थैले से 4 गेंदे उत्तरोत्तर पुनः वापस रखते हुए निकाली जाती है , तो इसी क्या प्रायिकता है कि उनमे से किसी गेंद अंक 0 नहीं लिखा हो ?
View Solutionयदि वक्र y=x3+ax−b के बिन्दु (1,−5) पर खींची गई स्पर्श रेखा , −x+y+4=0 रेखा पर लम्बवत हैं , तो निम्न में से कोण-सा एक बिन्दु वक्र पर स्थित हैं ?
View Solutionएक थैले में 1 से 20 तक अंकित गोलियाँ हैं। यदृच्छया एक गोली निकाली जाती है। एक अभाज्य संख्या अंकित गोली प्राप्त करने की प्रायिकता ज्ञात कीजिए।
View Solutionगंदले जल को एक पात्र में लेकर कुछ देर के लिए स्थिर रख देते हैं। अशुद्धियाँ पात्र की तल पर बैठ जाती है। इसके बाद स्वच्छ जल को अलग कर लेते हैं। इस प्रक्रिया को ..... कहते हैं।
View Solutionदाब बढ़ाने पर गैसें सिकुड़ जाती हैं।
View Solutionरेजाणीपानी में भीतर की चिनाई किस लकड़ी से जाती हैं?
View Solutionनिम्नलिखित शब्दों में से शुद्ध रूप शब्द के क्रमांक पर चिन्ह लगाइये।
View SolutionSOCl_2+HOHto[X]+[Y] निम्नलिखित में से कौन सा कथन गलत है/हैं? (I) उत्पादों में से एक गैस है जिसमें sp3d संकरण होता है। (II) दोनों उत्पाद प्रबल अम्ल होते हैं। (III) उत्पादों में से एक में Ppi-dpi बंध होता है। (IV) उत्पाद में से एक NH_3 के साथ अभिक्रिया करने पर श्वेत धूम देता है।
View Solutionनिम्नलिखित में से कितनी संरचनाएं एरोमैटिक हैं:
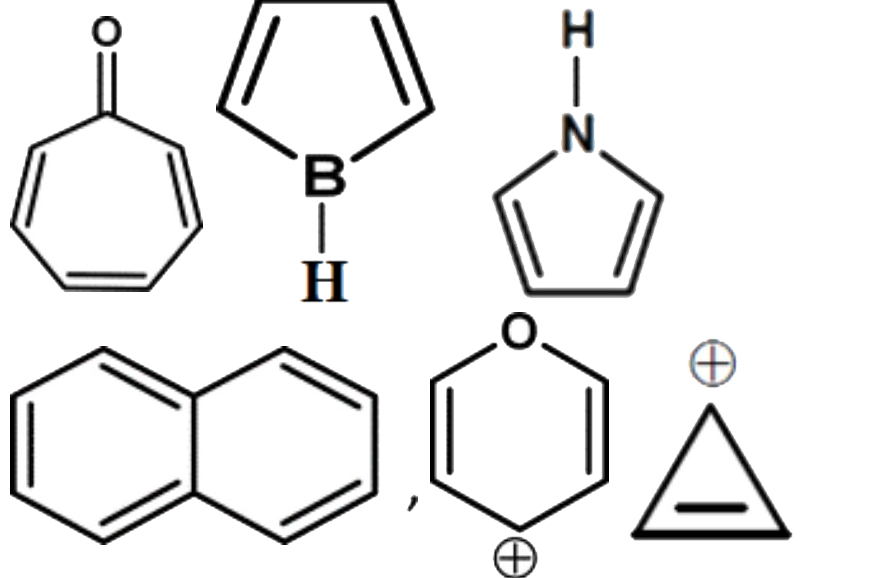
View Solutionएक अम्लीय जलीय विलयन में Mn^(2+), N i^(2+), Cu^(2+) और Hg^(2+) आयनों के मिश्रण में से H_2S पारित करने पर अवक्षेप प्राप्त होता हैं।
View SolutionX और Y तत्वों द्वारा निर्मित एक यौगिक एक घनीय संरचना में क्रिस्टलीकृत होता है। जिसमें परमाणु X घन के कोनों पर होते हैं और परमाणु Y दो गैर-आसन्न फलक केंद्रों पर होते हैं। यौगिक का सूत्र है
View Solutionनिम्नलिखित में से किस स्पीशीज में अधिकतम परमाणु एक ही तल में स्थित हो सकते हैं?
View Solutionनिम्नलिखित में से कितने प्रकाशिक सक्रिय हैं?
View Solution
