$\int \frac{x {tan}^{- 1} x}{{(1 + x^{2})}^{3 / 2} d x}$ का मान ज्ञात कीजिए ।

Video Solution

Text Solution

Verified by Experts

माना $x = tan θ$
$\Rightarrow θ = {tan}^{- 1} तथा d x = {sec}^{2} θ d θ$
$∴ \int \frac{x {tan}^{- 1} x}{{(1 + x^{2})}^{3 / 2}} d x = \int \frac{tan θ . θ}{{(1 + {tan}^{2} θ)}^{3 / 2}} . {sec}^{2} θ d θ$
$= \int \frac{θ tan θ}{{sec}^{3} θ} . {sec}^{2} θ d θ$
$\int \frac{θ tan θ}{sec θ} . d θ = \int θ I sin I I θ d θ$
$θ \int sin θ d θ - \int {\frac{d}{d θ} θ \int sin θ d θ} d θ$
$= θ (- cos θ) - \int (- cos θ) d θ$
$= - θ cos θ + \int cos θ d θ = - θ cos θ + sin θ + c$
$= cos θ (- θ + tan θ) + c$ ...(1)

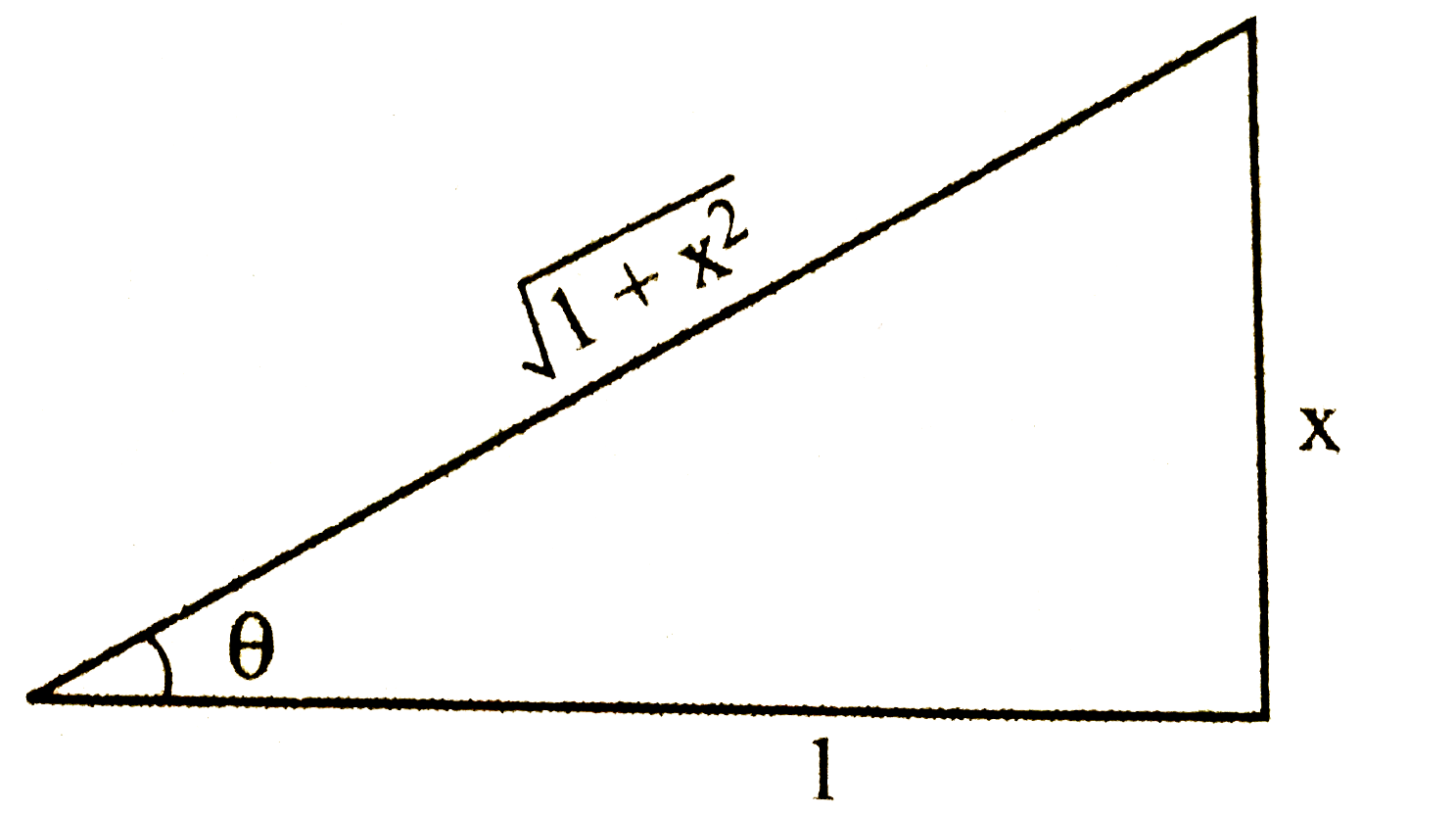
$\Rightarrow चूंकि x = tan θ तब θ = {tan}^{- 1} x$
$∴ cos θ = \frac{1}{\sqrt{1 + x^{2}}}$
ये मान समीकरण (1) में रखने पर,
$\int \frac{x {tan}^{- 1} x d x}{{(1 + x^{2})}^{3 / 2} = \frac{1}{\sqrt{1 + x^{2}}} . (- {tan}^{- 1} x + x) + c}$

|

Updated on:21/07/2023

Class 12 MATHS INTEGRALS

Topper's Solved these Questions

Similar Questions

BALAJI PUBLICATION-खण्डश: समाकलन -स्वमूल्यांकन परीक्षण

Home
Ask Doubt
Profile