आलेख व्दारा निम्न रैखिक प्रोग्रामन समस्या का हल ज्ञात कीजिए
निम्न अवरोधों के अन्तर्गत
2x+3y≤6
3x−2y≤6
y≤1
x,y≥0
z=8x+9y का अधिकतम मान ज्ञात कीजिए ।
सर्वप्रथम व्यवरोधों को समीकरणों में परिवर्तित करते हुए पाँच प्रतिबंध रेखाओं का ग्राफ खींचते हैं ।
2x + 3y = 6 में y = 0 ⇒ x = 3 तथा x= 0 ⇒ y = 2
∴ बिंदुओं (3, 0) व (0, 2) को मिलाने वाली रेखा 2x + 3y = 6 का ग्राफ प्राप्त करते हैं ।
इसी प्रकार बिंदुओं (2, 0) और (0, -3) को मिलाने वाली रेखा 3x−2y=6 का ग्राफ प्राप्त करते हैं जोकि 3x -2y = 6 में x = 0 ⇒ y = -3 तथा y = 0 ⇒ x = 2 रखने पर प्राप्त होते हैं
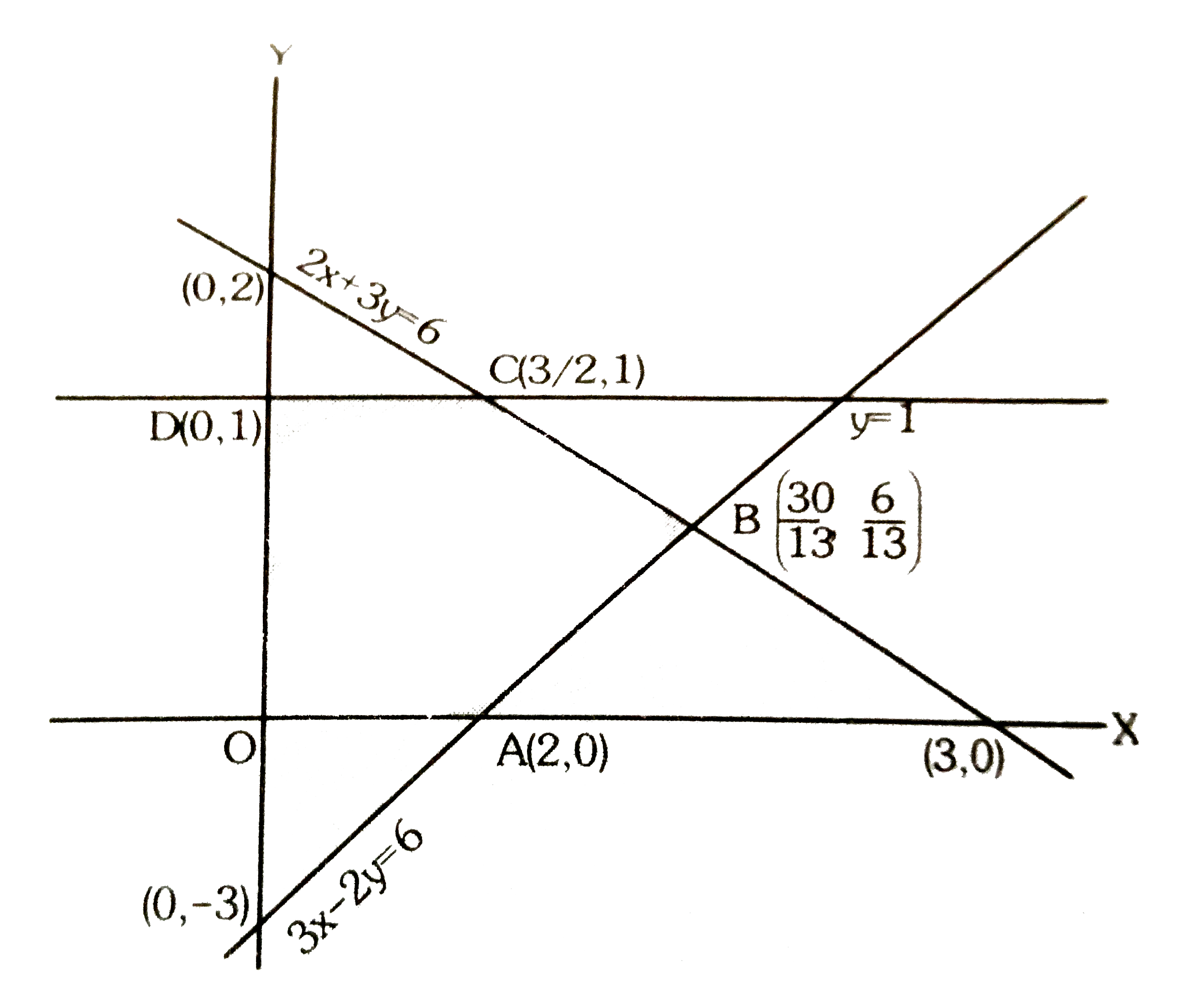 इस प्रकार हमें बंद उत्तल बहुभुज OABCD प्राप्त होता हैं जिसके शीर्ष O,A,B,C,D हैं ।
इस प्रकार हमें बंद उत्तल बहुभुज OABCD प्राप्त होता हैं जिसके शीर्ष O,A,B,C,D हैं ।
अतः उद्देश्य फलन z = 8x + 9y का महत्तम मान बहुभुज OABCD के कम - से - कम किसी एक शीर्ष पर होगा ।
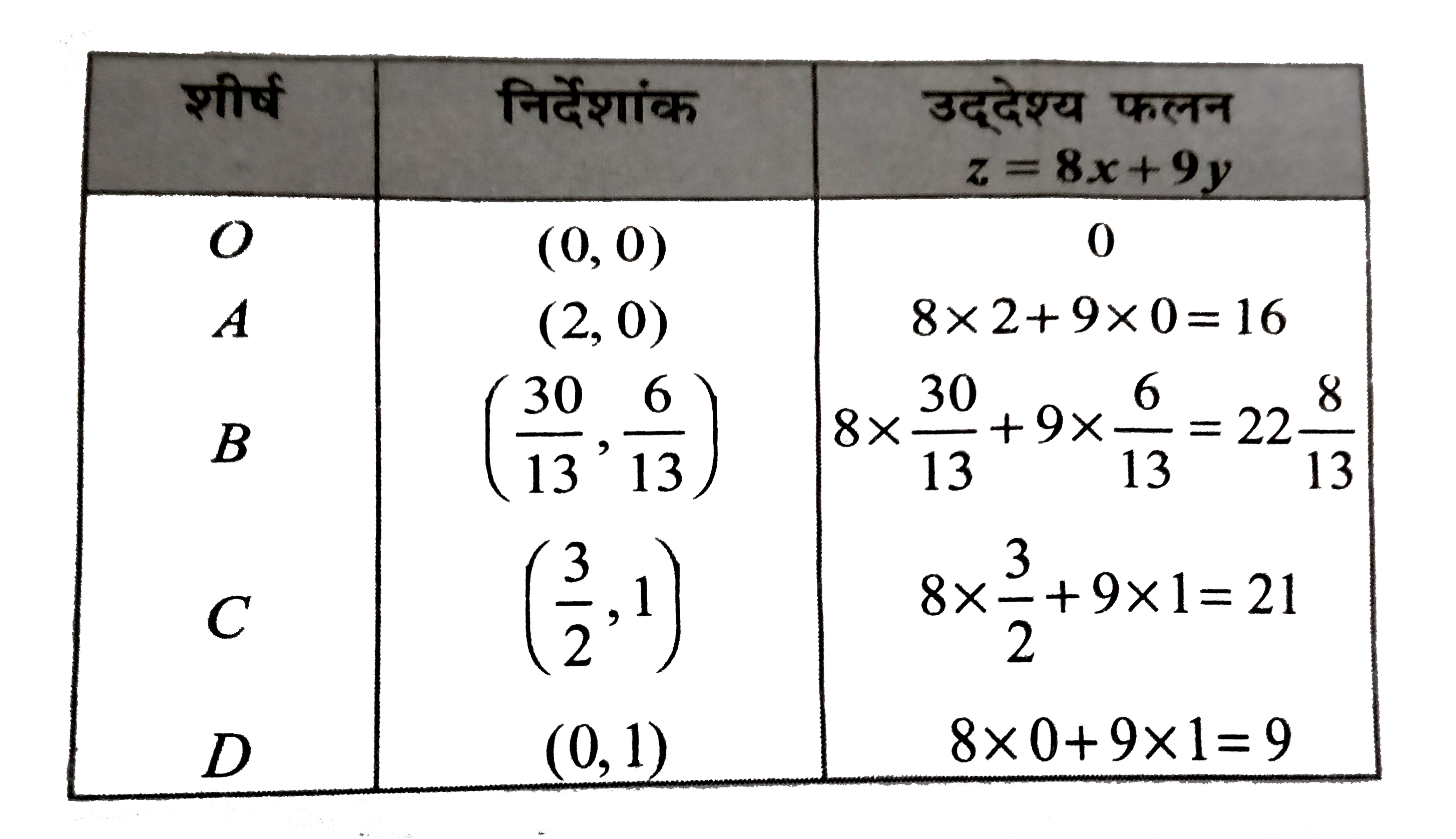
अतः इन पाँचो मानों में से z = 8x + 9y का महत्तम मान 22×813 , बिंदु B(3013613) पर प्राप्त होता हैं ।
इस प्रकार दिये गये प्रतिबंधों के आधीन z = 8x + 9y का महत्तम मान 22×813 हैं , और यह तब प्राप्त होता हैं जब x=3013,y=613 हैं ।
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - बहुविकल्पीय प्रश्न
13 Videos
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - अभ्यास प्रश्न 23.1
8 Videos
- प्रायिकता क्रमश:BOOK - BALAJI PUBLICATIONCHAPTER - प्रायिकता क्रमश:EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- संबंध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - संबंध एवं फलन EXERCISE - अभ्यास प्रशन 1.3
7 Videos
Similar Questions
रैखिक प्रोग्रामन समस्या निम्न व्यवरोधों के अन्तर्गत x1+2x2≤2000,x1+x2≤1500,x2≤600 और x1,x2≥0 हैं तो कौन - सा बिंदु घिरा हुए धन भाग में नही हैं ?
View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
3x1+2x2≤12
5x1≤1
x1+x2≥8
−x1+x2≥4
तथा x1,x2≥0
अधिकतम z=x1+12x2
View Solutionएक प्रश्न-पुस्तिका में 300 सरल सत्य/असत्य प्रश्न, 200 कठिन सत्य/असत्य प्रश्न, 500 सरल बहुविकल्पीय प्रश्न तथा 400 कठिन बहुविकल्पीय प्रश्न है | यदि प्रश्न-पुस्तिका से एक प्रश्न का चयन यदृच्छया किया जाता है | सिद्ध कीजिए कि इस प्रश्न के सरल होने की प्रायिकता 59 है जबकि यह एक बहुविकल्पीय प्रश्न है |
View Solutionवास्तविक संख्याओं के समुछ्य R में प्राचित्रण f(x)=sinx,x∈R तथा g(x)=x2,x∈R द्वारा परिभाषित है सिद्ध कीजिय की gof≠fog
View SolutionThe value of |[a,a+d,a+2d] , [a+d,a+2d,a+3d] , [a+2d,a+3d,a+4d]|+|[b
View Solutionनिम्न व्यवरोधों के अन्तर्गत Z=3x+2y का न्यूनतमीकरण कीजिए
x+y≥8,3x+5y≤15 तथा x,y≥0
View Solutionव्यवरोधों 2x+y≤6,x≤2,x≥0,y≥0के अन्तर्गत Z=11x+7y का अधिकतम मान निर्धारित कीजिए |
View SolutionThe correct order of size among Br^(+), Br, Br^(-)
View Solutionनिम्न असामिकाओ का आलेखीय विधि से हल ज्ञात कीजिए-
|x|≤3
View Solutionनिम्नलिखित असमिकाओं के निकाय के हलों का डोमेन ज्ञात कीजिए :
x≥2,x+2y≤2,x−y+1≤0.
View Solutionनिम्न फलनों के उच्चिष्ठ का निम्निष्ठ मान ज्ञात कीजिए -
(x−1)2ex
View Solutionनिम्न समतलो के मध्य कोण ज्ञात कीजिए -
x+y−2z=3 और 2x−2y+z=5
View Solutionनिम्न समस्या को हल कीजिए :
Z=6x−2y का अधिकतम मान ज्ञात कीजिए जबकि
2x−y≤2,x≤3,x≥0,y≥0
View Solutionनिम्न रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल कीजिए।
निम्नतम Z=200x+500y
व्यवरोध x+2y≥10
3x+4y≤24
तथा x≥0,y≥0
View Solutionनिम्न रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल कीजिए।
अधिकतम Z=y+34x
व्यवरोध x−y≥0
−x2+y≤1
तथा x≥0,y≥0
View Solutionनिम्न रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल कीजिए।
अधिकतम Z=2x+3y
व्यवरोध 4x+6y≤60
2x+y≤20
तथा x≥0,y≥0
View Solution
