एक उत्पादन के कारखाने में तीन मशीनें I, II और III लगी हैं । मशीन I और II अधिकतम 12 घण्टे तक चलाए जाने की क्षमता रखती हैं । जबकि मशीन III प्रतिदिन कम - से - कम 5 घण्टे चलनी चाहिए । निर्माणकर्ता केवल दो प्रकार के सामान M और N का उत्पादन करता हैं । जिनमें प्रत्येक के उत्पादन में तीनों मशीनों की आवश्यकता होती हैं । M और N के प्रत्येक उत्पाद के एक नग उत्पादन में तीनों मशीनों के संगत लगा समय (घण्टों में ) निम्नलिखित सारणी में दिया गया हैं -

वह उत्पाद M पर 600 रुपये प्रति नग और उत्पाद N पर 400 रुपये प्रति नग की दर से लाभ कमाता हैं । मानते हुए कि उसके सभी उत्पाद बिक जाते हैं , जिनका उत्पादन किया गया हैं , तब ज्ञात कीजिए कि प्रत्येक उत्पादन के कितने नगों का उत्पादन किया जाये जिससे लाभ का अधिकतमीकरण हो अधिकतम लाभ क्या होगा ?
मान लीजिए कि उत्पाद M और N के नगों की संख्या क्रमशः x और y हैं ।
उत्पादन पर कुल लाभ = (600x + 400y ) रुपये
इस समस्या का गणितीय रुप निम्न हैं -
z = 600x + 400y का अधिकतम मान ज्ञात कीजिए ।
जहाँ व्यवरोध निम्नलिखित हैं -
x+2y≤12 (मशीनों पर व्यवरोध ) ...(1)
2x+y≤12 (मशीन पर व्यवरोध) ....(2)
x+54y≥5 (मशीनों पर व्यवरोध) ...(3)
x≥0,y≥0 ....(4)
असमिकाओं (1) से (4) तक के ग्राफ व्दारा घिरा सुसंगत क्षेत्र ABCDE (छायांकित) हैं । स्पष्ट है कि सुसंगत क्षेत्र परिबध्द हैं , कोणीय बिंदुओं A , B, C, D और E के निर्देशांक क्रमशः (5,0) , (6,0),(4,4) , (0,6) और (0,4) हैं ।

इन कोणीय बिंदुंओं पर z = 600x + 400y का मान निम्नलिखित हैं -
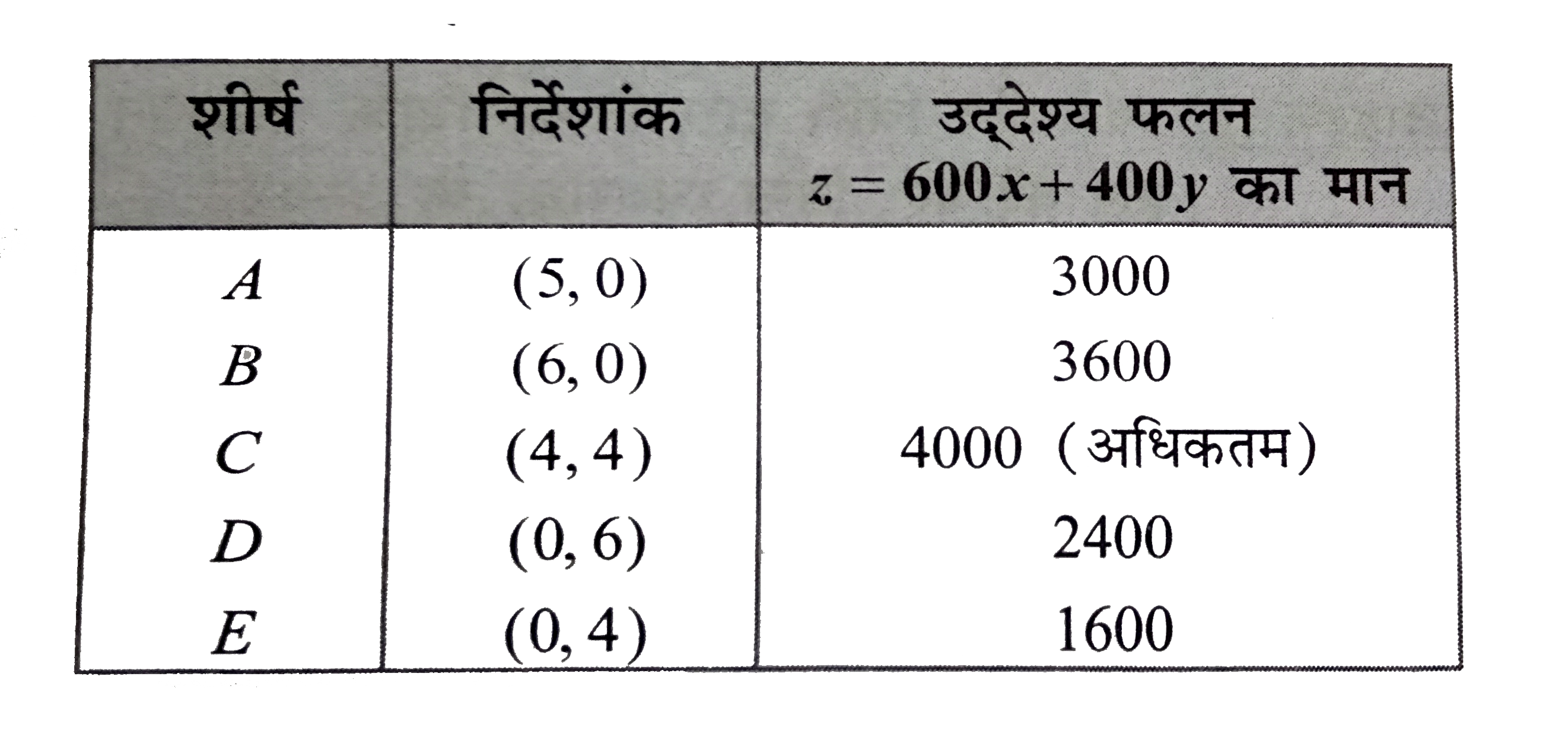
अतः बिंदु (4,4) पर z का अधिकतम मान हैं । अतः उत्पादक को अधिकतम 4000 रुपये लाभ कमाने के लिए प्रत्येक उत्पाद के 4 नगों का उत्पादन करना चाहिए ।
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - बहुविकल्पीय प्रश्न
13 Videos
- रैखिक प्रोग्रामनBOOK - BALAJI PUBLICATIONCHAPTER - रैखिक प्रोग्रामनEXERCISE - अभ्यास प्रश्न 23.1
8 Videos
- प्रायिकता क्रमश:BOOK - BALAJI PUBLICATIONCHAPTER - प्रायिकता क्रमश:EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
- संबंध एवं फलन BOOK - BALAJI PUBLICATIONCHAPTER - संबंध एवं फलन EXERCISE - अभ्यास प्रशन 1.3
7 Videos
Similar Questions
रैखिक प्रोग्रामन समस्या निम्न व्यवरोधों के अन्तर्गत x1+2x2≤2000,x1+x2≤1500,x2≤600 और x1,x2≥0 हैं तो कौन - सा बिंदु घिरा हुए धन भाग में नही हैं ?
View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
3x1+2x2≤12
5x1≤1
x1+x2≥8
−x1+x2≥4
तथा x1,x2≥0
अधिकतम z=x1+12x2
View Solutionएक प्रश्न-पुस्तिका में 300 सरल सत्य/असत्य प्रश्न, 200 कठिन सत्य/असत्य प्रश्न, 500 सरल बहुविकल्पीय प्रश्न तथा 400 कठिन बहुविकल्पीय प्रश्न है | यदि प्रश्न-पुस्तिका से एक प्रश्न का चयन यदृच्छया किया जाता है | सिद्ध कीजिए कि इस प्रश्न के सरल होने की प्रायिकता 59 है जबकि यह एक बहुविकल्पीय प्रश्न है |
View Solutionवास्तविक संख्याओं के समुछ्य R में प्राचित्रण f(x)=sinx,x∈R तथा g(x)=x2,x∈R द्वारा परिभाषित है सिद्ध कीजिय की gof≠fog
View Solutionएक निर्माणकर्ता का मानना है की पुरुष और महिला मजदूरों की दक्षता समान होती है| अतएव वह उन्हें एक ही दर से मजदूरी देता है| उसके पास 30 मात्रक (units ) मजदूर और 17 मात्रक पूंजी है| जिसका वह A और B दो प्रकार के माल के उत्पादन में प्रयोग करते है|A के एक मात्रक उत्पादन में 2 मजदूर और 3 मात्रक पूंजी आवश्यकता है, जबकि B के एक मात्रक उत्पादन में 3 मजदूर और 1 मात्रक पूंजी आवश्यक है| A के एक मात्रक का मूल्य रु 100 तथा B के एक मात्रक का मूल्य रु 120 है | वह अपने साधनो का उपयोग किस प्रकार करें ताकि अधिकतम आय हो? क्या आप निर्माणकर्ता के इस दृष्टिकोण (विचार) से सहमत है की पुरुष और महिला मजदूरों की क्षमता समान होती है अतएव उन्हें एक ही दर से मजदूरी देनी चाहिए?
View Solutionएक टी. वी बनाने के कारखाने में मशीने A,B और C कुल उत्पादन का क्रमशः 30 % और 50 % टी .वी बनाती है। इन मशीनो के उत्पादन का क्रमशः 7% , 5 % और 2% टी . वी खराब (त्रुटिपूर्ण ) पायी जाती है। टी .वी के कुल उत्पादन में से एक टी वी यदृच्छया जाँच के लिए निकाला गया है और वह खराब (त्रुटिपूर्ण ) पाया गया है। इसकी प्रायिकता ज्ञात कीजिए कि वह मशीन A द्वारा बनाया गया है।
View Solutionचलों जानते हैं संयोग और प्रायिकता के बारे में....
View SolutionThe table shows the production of different types of cars (in thousands). यह तालिका अलग-अलग प्रकार के कारों का उत्पादन ( हज़ार में) दर्शाती है | What is the ratio of the total production of cars of type A in 2014 and type C in 2013 taken together to the total production of cars of type B in 2016 and type E in 2015 taken together? 2014 में A प्रकार की कारों और 2013 में C प्रकार की कारों के कु ल उत्पादन का 2016 में B प्रकार की कारों और 2015 में E प्रकार की कारों के कुल उत्पादन के साथ अनुपात ज्ञात करें |
View Solutionलीथियम की तुलना में सोडियम और पोटैशियम जल के साथ अत्यधिक तीव्रता से अभिक्रिया करते हैं,
View SolutionNO_2 और N_2O_4 नाइट्रोजन डाइऑक्साइड के दो रूप हैं। एक गैसीय अवस्था में मौजूद होता है जबकि दूसरा द्रव अवस्था में। NO_2 और N_2O_4 रूपों की प्रकृति है:
View Solutionघन आधारित एकक कोष्ठिका में कितने परमाणु हैं, जिसके प्रत्येक कोने पर एक परमाणु है और घन के प्रत्येक काय विकर्ण पर दो परमाणु हैं?
View Solutionनिम्नलिखित में से किसमें ध्रुवीय और असमतलीय दोनों प्रकार के बंध उपस्थित होते हैं?
View Solutionबोरिक अम्ल में बोरॉन और ऑक्सीजन परमाणुओं के संकरण की अवस्था क्रमशः हैं:
View Solutionनिम्नलिखित में से कौनसा LiAIH4 के साथ अपचयन पर केवल एक उत्पाद का उत्पादन करेगा?
View Solutionनिम्नलिखित में से प्रशांतक और शामक के रूप में उपयोग की जाने वाली औषधियाँ हैं:
View Solutionएक कार्बनिक यौगिक के 0.2 g में C, H और O उपस्थित होते हैं। दहन करने पर, यह 0.15 g CO2 और 0.12 g H2O का उत्पादन करता है। C, H और O का प्रतिशत क्रमश: है:
View Solution
