Question

एक सेवानिवृत्त व्यक्ति 50000रुपये का निवेश करना चाहता हैं । उसके ब्रॉकर ने उसे दो तरह के बाण्डस A तथा B जिसमें निवेशित धन पर क्रमशः 10% और 9% रिटर्न मिलता हैं , में निवेश करने की सिफारिश की । उसने कम से कम 20000 रुपये बाण्ड A तथा कम से कम 10000 रुपये बाण्ड B में निवेश करने का निर्णय किया । वह बाण्ड A में कम से कम बाण्ड B जितना ओर निवेस करता चाहता हैं । अधिकतम रिटर्न के लिए दी गई रैखिक प्रोग्रामन समस्या को आलेखनीय विधि से हल कीजिए ।

Explanation

माना व्यक्ति व्दारा A बाण्ड तथा बाण्ड B में निवेशित धनराशि Rs. x और Rs. y हैं ।
Max. z = x का 10% + y का 9%
z - 0.1x + 0.9y का निम्नलिखित व्यवरोधों के निकाय
`x + y = 50000`
`x ge y` , `x - y ge 0`
`x ge 20000 ` और `y ge 10000`
के अन्तर्गत अधिकतमीकरण करो ।
अब हम रेखाओं का आलेख खींचते हैं -

x + y = 50000 ...(1)
x - y = 0 ...(2)
x = 20000 ... (3)
तथा y = 10000 ...(4)

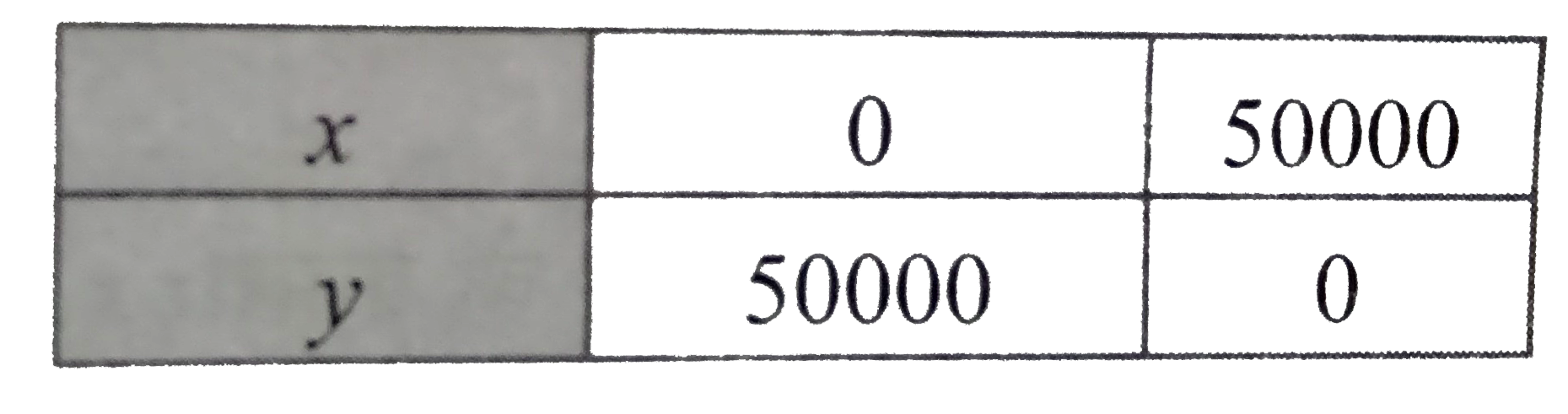
यह बिन्दुओं ( 0 , 50000) तथा (50000,0) से होकर गुजरती हैं । रेखा x - y = 0 के लिए सारणी हैं -

यह बिन्दुओं (0,0) तथा (20000,20000) से होकर गुजरती हैं ।
असमीकरण `x ge y` में (10000 , 0) रखने पर
`10000 ge 0` (सत्य )
इसलिए अर्ध्दसमतल X- अक्ष की तरफ है ।
रेखा x = 20000, X- अक्ष के लम्बवत् हैं ।
असमीकरण `x ge 20000` में (0,0) रखने पर
`0 ge 20000` (असत्य )
इसलिए अर्ध्दसमतल मूल बिंदु से दूर हैं ।
रेखा y = 10000, Y- अक्ष के लम्बवत् हैं ।
असमीकरण `y ge 10000` में (0,0) रखने पर -
` 0 ge 10000` (असत्य)
इसलिए अर्ध्दसमतल मूल बिंदु से दूर हैं ।
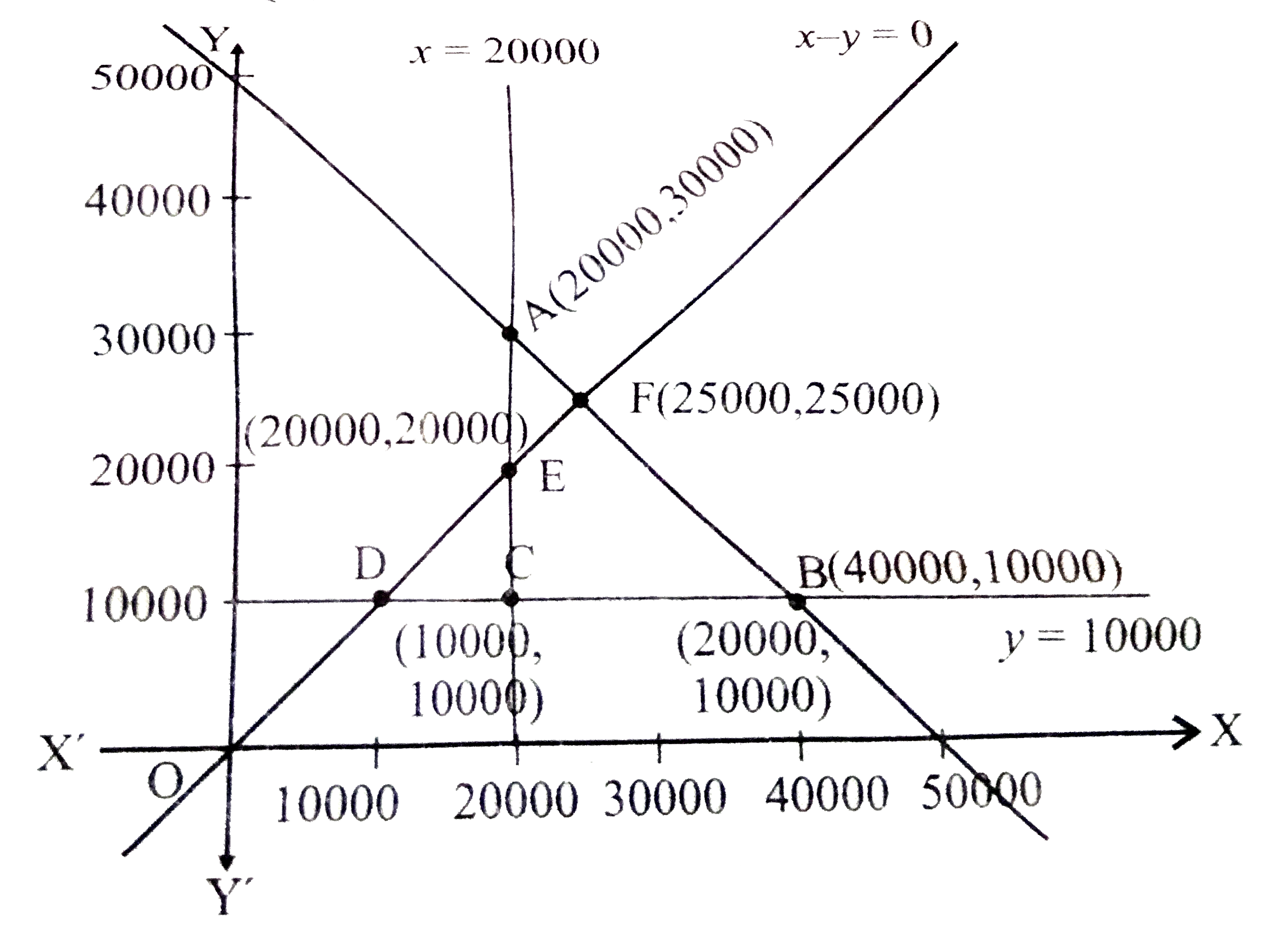
स्पष्टतः रेखा (1) , (2) , (3) तथा (4) के प्रतिच्छेदन बिंदु हैं -
A(20000, 30000) , B(40000, 10000)
C(20000 , 10000) , D(10000, 10000) , E(20000, 20000) , F(25000,25000)
आलेख स स्पष्ट हैं कि सुसंगत क्षेत्र रेखाखण्ड BF पर हैं । सुसंगत क्षेत्र के कोणीय बिंदु B(40000,10000) तथा F(25,000 , 25000) हैं ।
कोणीय बिंदु पर z का मान -

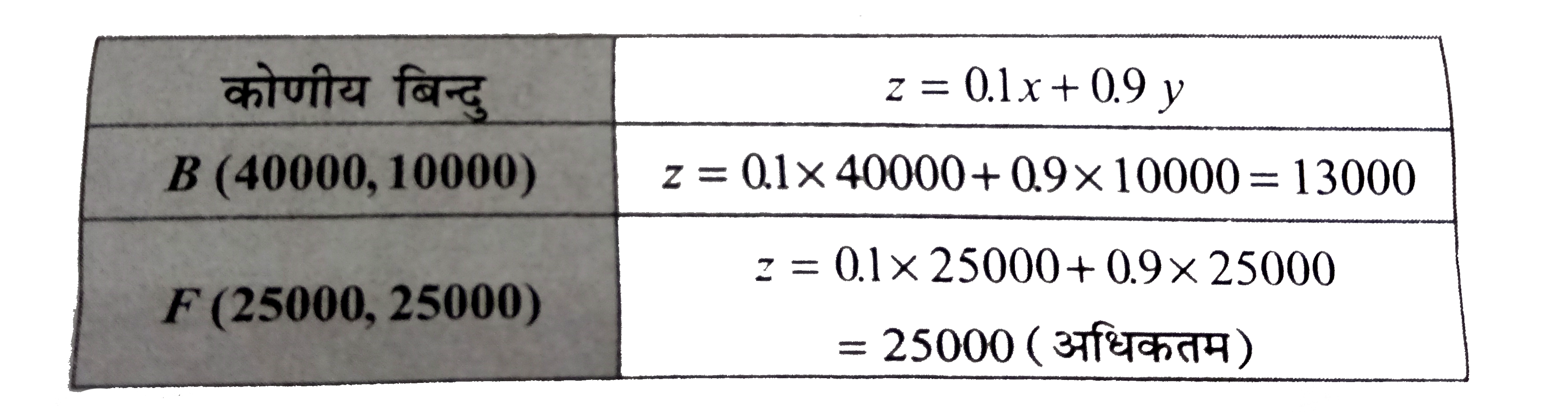
अतः अधिकतम रिटर्न के लिए उसे प्रत्येक ब्रांड में 25000 रुपये निवेश करने होंगे ।