एक कण जिसके स्थिति सदिश r के x,y,z-अक्षो के अनुदिश अवयव क्रमश: x,y,z है और रखिये सवेग सदिश के अवयव px,py,pz है कोनिये सवेग L के अक्षो के अनुदिश अवयव ज्ञात कीजिएः। दर्शाइए की यदि कण केवल x-yतल में ही गतिमान हो, तो कोनिये सवेग का केवल z -अवयव ही होता है
माना कण बिंदु P पर स्थित है, इसका स्थिति सदिश r तथा रखिये सवेग P है
r=xˆi+yˆj+zˆk
p=pxˆi+pyˆj+pzˆk
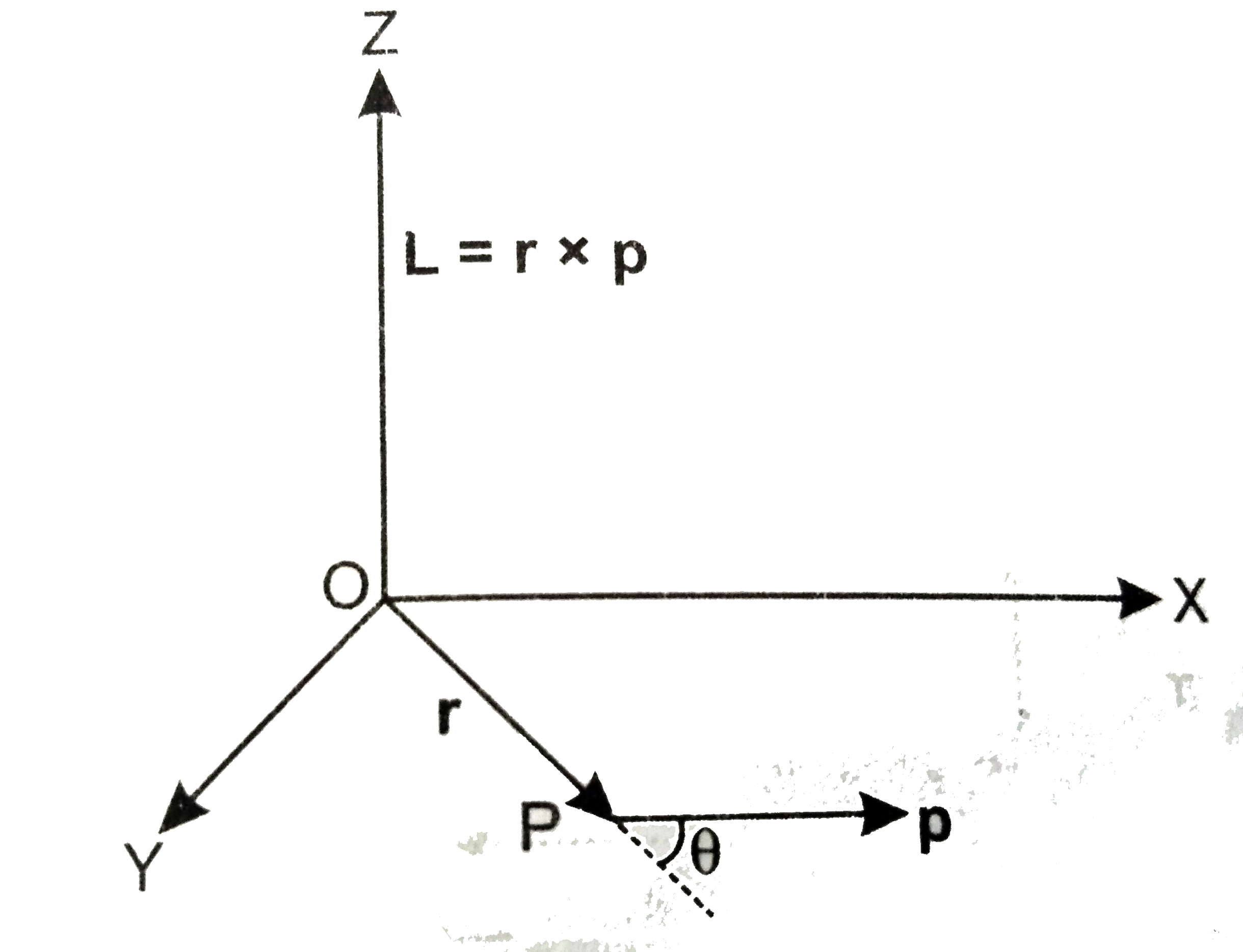
सदिश का कोणीय सवेग L=r×p
=(xˆi+yˆj+zˆk)×(pxˆi+pyˆj+pzˆk)
=∣∣
∣
∣∣ˆiˆjˆkxyzpxpypz∣∣
∣
∣∣
यदि X,Y तथा Z के अनुदिश L के अवयव क्रमश Lx,Ly तथा Lz है तब Lxˆi+Lyˆj+Lzˆk=ˆi(ypz−zpy)+ˆj(zpx−xpz)+ˆk(xpy−ypx)
दोनों पक्षों की तुलना करने पर Lx=ypz−zpy
Ly=zpx−xpz
Lz=xpy−ypx
प्रशानुसार, कण X-Y तल में गति कर रहा है
∴ X-Y तल में गतिमान कण द्वारा बल आघूर्ण τz=τFy−τFx.....(i)
जहाँ τzX−Y तल में गतिमान कण पर Z-अक्ष के के अनुदिश बल का आघूर्ण का अवयव है
माना तल में द्रव्यमान के कण का वेग v है तथा तथा इसके X तथा Y अक्ष के अनुदिश वेग है न्यूटन के द्वितीय नियम से Fx=ddt(px)=ddx(mvx)
=mdvxdt
तथा Fy=ddt(py)=mdvydt
τz=xmddt(vx)−ymddt(vy)
=m[xdvydt−dvxdty].....(ii)
अब ddt[xvy−yvx)=ddt(xvy)−ddt(yux)
=[xddtvy+vyddtx]−[yddtvx+vxddty]
=xddtvy+vxvy−yddtvx−vxvy
=xddtvy−yddtvx......(iii)
समीकरण (i) व (iii) से
=τz=mddt(xvy−yux)
=ddt(xmvy−ymvx).....(iv)
∴py=mvyतथा px=mvx(therefore "सवेग" p=mv)<br>therefore tau_(z)=d/dt(xp_(y)-yp_(x))<br>tau_(z)=d/dttau_(z) [समीकरण (ii) के भाग (a) से]
उपरोक्त सम्बन्ध से हम इस निष्कर्ष पर पहुंचते है की यदि कण X-Yतल में गतिमान हो, तो कोणीय सवेग (L) का केवल Z-अवयव ही होता है
Topper's Solved these Questions
- घूर्णन गतिBOOK - BALAJI PUBLICATIONCHAPTER - घूर्णन गतिEXERCISE - अतिरिक्त अभ्यास
20 Videos
- घूर्णन गतिBOOK - BALAJI PUBLICATIONCHAPTER - घूर्णन गतिEXERCISE - बहुविकल्पीय प्रश्न
23 Videos
- घर्षण BOOK - BALAJI PUBLICATIONCHAPTER - घर्षण EXERCISE - बहुविकल्पीय प्रश्न
18 Videos
- डॉप्लर प्रभाव BOOK - BALAJI PUBLICATIONCHAPTER - डॉप्लर प्रभाव EXERCISE - बहुविकल्पीय प्रश्न
15 Videos
Similar Questions
सलग्न चित्र में दिखाया गया है की एक खड़ी होने वाली सीढ़ी के दो पक्षों BA और CA की लम्बाई 1 .6 मीटर है और इनको A पर कब्ज़ा लगा कर जोड़ा गया है| इन्हे ठीक बिच में 0 .5 मीटर लम्बी रस्सी DE द्वारा बाँधा गया है| सीढ़ी BA के अनुदिश B से 1 .2 मीटर की दुरी पर स्थित बिंदु F से 40 किग्रा का एक भार लटकाया गया है|यह मानते हुए की फर्श घर्षणरहित है और सीढ़ी का भार उपेक्षणीय है, रस्सी में तनाव और सीढ़ी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए|
(g=9.8 मीटर /सेकंड 2 लीजिए)
View Solutionजड़त्व आघूर्ण कैसी राशि है?
View Solutionघर्षण बल है
View Solutionडॉप्लर प्रभाव लागु होता है -
View Solutionयदि मूलबिंदु O के सापेक्ष त्रिभुज ABC के शीर्षों के स्थिति सदिश क्रमशः (1,−1,2),(2,1,3) और (−1,2,−1) है| तथा इसके केन्द्रक का स्थिति सदिश ज्ञात कीजिए|
View Solutionसदिशों →a=2ˆi+4ˆj−5ˆk और →b=λˆi+2ˆj+3ˆk के योग के अनुदिश एकांक सदिश के साथ सदिश ˆi+ˆj+ˆk का अदिश गुणनफल 1 के बराबर होता है। λ का मान ज्ञात कीजिए।
View Solutionयदि बिंदु A जिसका स्थिति सदिश ¯a+2¯b है तथा सदिश ¯a,AB को 2:3 के अनुपात में विभाजित करता है तो B का स्थिति सदिश है:
View Solutionयदि किसी त्रिभुज के शीर्षो के स्थिति सदिश क्रमश: →a,→b,→c हो तो इस त्रिभुज के केन्द्रक का स्थिति सदिश होगा -
View Solutionएक सदिश ¯r,X,Y तथा Z-अक्षो के साथ क्रमश: 45∘, 60∘, 120∘ के कोण बनता है। यदि सदिश ¯r का परिमाण 2 इकाई है तो ¯r ज्ञात कीजिए।
View Solutionएक सदिश →r, x- अक्ष के साथ 45∘ और y- अक्ष के साथ 60∘ को बनाता है यदि |→r|=10 तो सदिश →r ज्ञात कीजिए।
View Solutionएक सदिश x- अक्ष v y-अक्ष प्रत्येक के साथ π4 कोण बनाता है, तो z-अक्ष के साथ यह क्या कोण बनाता है ?
View Solutionयदि एक द्वितीय क्रम के सारणिक का प्रत्येक अवयव शून्य या एक हो तो सारणिक का मान धनात्मक होने की क्या प्रायिकता है ? ( यह मानते हुए कि सरणिक के प्रत्येक अवयव को स्वतंत्र रूप से चुना जा सकता है तथा प्रत्येक के चुने जाने कि प्रायिकता 12 है । )
View Solutionयदि निकाय के समीकरणों x−ky−z=0,kx−y−z=0 तथा x+y−z=0 का एक अशून्य हल है, तो k का संभावित मान होगा
View Solutionमाना R3 में p, q और r तीन असमतलीय सदिश हैं। माना सदिश s के घटक क्रमागत सदिशों p, q एवंr के अनुदिश क्रमशः 4, 3 और 5 हैं। यदि s के घटक क्रमागत सदिशों (−p+q+r),(p−q+r) एवं (−p−q+r) के अनुदिश क्रमशः x,y और z हैं, तब 2x+y+z का मान है।
View Solutionसमुच्चय || समुच्चय के अवयव || उदाहरण
View SolutionIf x+y+z=19, x2+y2+z2=133 and xz=y2, then the difference between z and x is :
यदि x2+y2+z2=133 तथा xz=y2 है, तो z और x के बीच क्या अंतर है ?
View Solution
