सरल आवर्त गति करते किसी कण कि गति का वर्णन नीचे दिए गये विस्थापन फलन किया जाता है - ,
x(t)=Acos(ωt+ϕ) यदि कण कि आरंभिक (t=0 ) स्थिति सेमी तथा उसका आरम्भिवेग सेमी /सेकंड है , तो कण का आयाम तथा आरम्भिक कला कौन क्या है ? कण कि कोणीय आवृत्ति सेकंड है । यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या ( cos) फलन के स्थान पर हम ज्या ( sin) फलन चुनेः x=Bsin(ωt+α) तो उपरोक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला कौन क्या होगा ?
दिया है - x(t)=Acos(ωt+ϕ)
t = 0 पर विस्थापन x(t)=1 सेमी तथा वेग υ=ω सेमी / सेकण्ड
कोणीय आवृत्ति ω=πसेकण्ड−1 या 1=Acos(ωt+ϕ)
t = 0 पर , 1=Acosϕ
अब ,υ(t)=dxdt(t)=ddtAcos(ωt=ϕ)
=−Aωsin(ωt+ϕ)
पुनःt = 0 पर , v=ω सेमी/सेकण्ड
या ω=0Aωsinϕ
या −1=Asinϕ ...(ii)
समीकरण (i ) तथा समीकरण (ii ) का वर्ग करके जोड़ने पर ,
A2cos2ϕ+A2sin2ϕ=(1)2+(−1)2
A2=2
या A=±√2
अतः आयाम=√2 सेमी
समीकरण (ii ) को समीकरण (i ) से विभाजित करने पर ,
AsinϕAcosϕ=−11
या tanϕ=−1
या ϕ=−π4 या 7π4
cos फलन के स्थान पर sin फलन प्रयुक्त करने पर
x(t)=Bsin(ωt+α)
Bsinα=1 ...(iii)
वेग υ(t)=dx(t)dt=ddt[Bsin(ωt+α)]
=+Bωcos(ωt+α)
पुनः t=0, υ(t)=ω सेमी/सेकण्ड
ω=+Bω(0+α)
Bcosα=+1 ...(iv)
समीकरण (iii ) तथा समीकरण (iv ) का वर्ग करके जोड़ने पर ,
B2sin2α+B2cos2α=(1)2+(+1)2
या B2sin2α+B2cos2α=2
B2(sin2α+cos6(2)α)=2
B2⋅1=2
या B=±√2 सेमी
अतः गति का आयाम=√2 सेमी
समीकरण (iii ) को समीकरण (iv ) से भाग देने पर ,
BsinαBcosα=11 या tanα=1
∴α=π4
Topper's Solved these Questions
- दोलन BOOK - BALAJI PUBLICATIONCHAPTER - दोलन EXERCISE - अतिरिक्त अभ्यास
6 Videos
- दोलन BOOK - BALAJI PUBLICATIONCHAPTER - दोलन EXERCISE - बहुविकल्पीय प्रश्न
36 Videos
- तरलों के यांत्रिक गुण (2):तरल गतिकी BOOK - BALAJI PUBLICATIONCHAPTER - तरलों के यांत्रिक गुण (2):तरल गतिकी EXERCISE - पाठ्य -पुस्तक के प्रश्न
44 Videos
- द्रव के तापीय गुणBOOK - BALAJI PUBLICATIONCHAPTER - द्रव के तापीय गुणEXERCISE - पाठ्य-पुस्तक के प्रश्न
22 Videos
Similar Questions
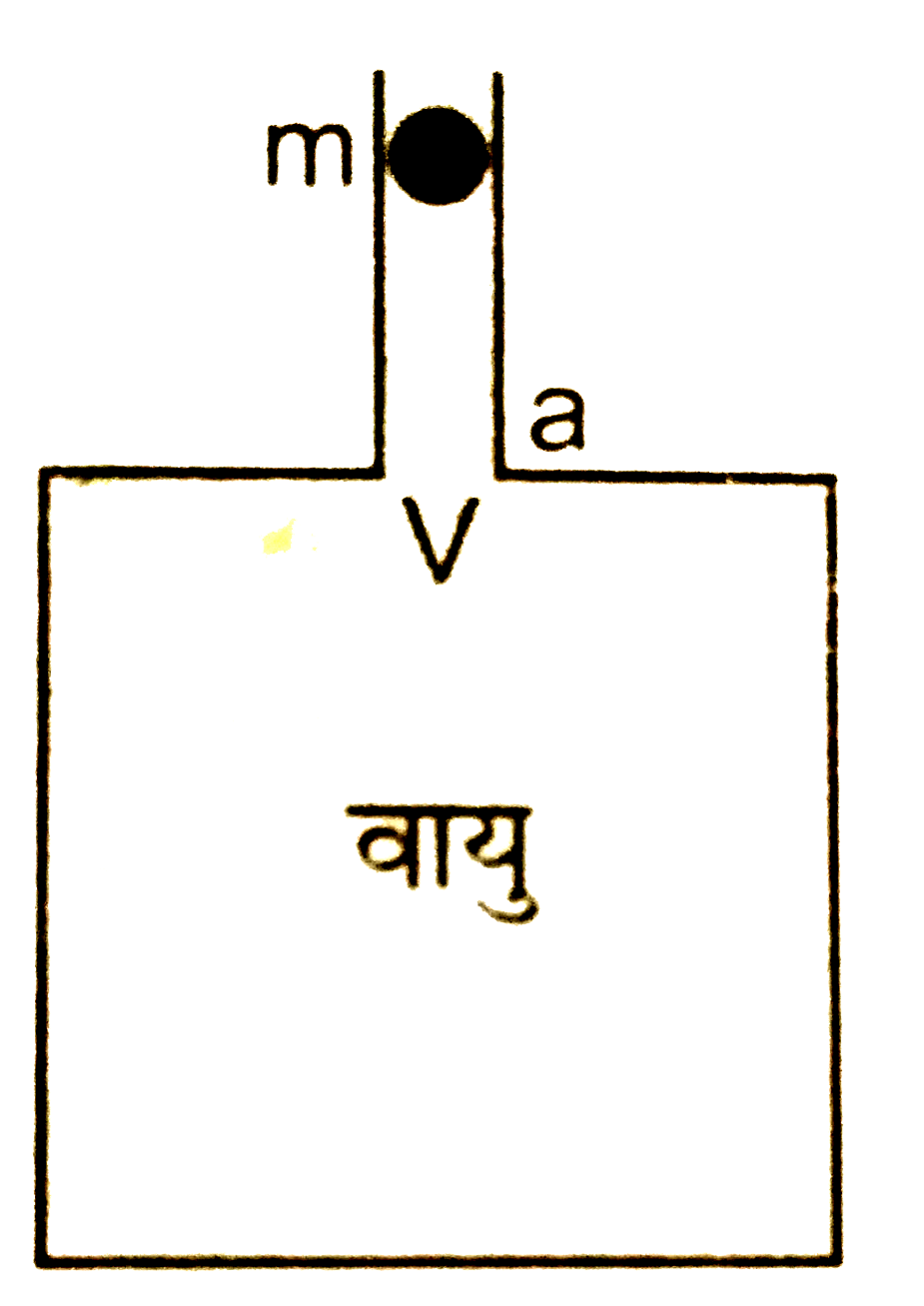
चित्र में दर्शाये अनुसार V आयतन के किसी वायु कक्ष कि ग्रीवा ( गर्दन) कि अनुप्रस्थ काट का क्षेत्रफल a है । इस ग्रीवा में m द्रव्यमान कि कोई गोली घर्षण के ऊपर - नीचे गति कार सकती है । यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते है , तो वह सरल आवर्त गति करती है । दाब - आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए ।
View Solutionकौन- सी गति सरल आवर्त गति है ?
View Solutionमस्तिष्क की अपेक्षा मानव का पैरों पर रक्त चाप अधिक होता है ?
View Solutionनिऑन तथा CO2 के त्रिक बिन्दु क्रमशः 24.57K तथा 216.55 K है। इस तापो को सेल्सियस तथा फॉरेनहाइट मापक्रमों में व्यक्त कीजिए।
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionचित्र में AB ,BC तथा CA वृत्त कि स्पर्श रेखाएं है। यदि BC=6.3 सेमी तथा MC=2.7 सेमी हो ,तो BL कि नाप लिखिए।

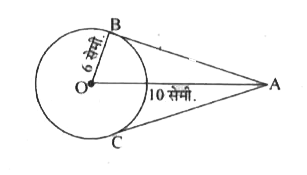
View Solutionदिये गये चित्र में O वृत्त का केंद्र है। AB व AC वृत्त कि स्पर्श रेखाएं है। यदि OA=10 सेमी तथा OB=6 सेमी है तो AC कि लम्बाई लिखिए।
View Solutionयदि फलन f (x) आवर्त का सतत फलन है , तो समाकलन I=∫a+Taf(x)dx का मान है
View Solutionअल्फा कण प्रकीर्णन तथा परमाणु का रदरफोर्ड का नाभिकीय मॉडल
View Solutionअल्फा कण प्रकीर्णन तथा ,परमाणु का रदरफोर्ड मॉडल
View Solutionविद्युत कण संचलन तथा स्कंदन
View Solutionचुम्बकीय क्षेत्र में आवेशित कण की गति
View Solutionचुंबकीय क्षेत्र में आवेशित कण की गति
View Solutionदोलन| सरल आवर्त गति का विस्थापन समीकरण
View Solutionचुम्बकीय क्षेत्र में आवेशित कण की गति
View Solutionचुम्बकीय क्षेत्र में आवेशित कण की गति
View Solution
