तीन कण A , B और C किसी समय t = 0 पर d भुजा वाले समबाहु ABE के शीर्ष बिंदुओ पर है । सभी कण हर समय v चल से चलते है ।A के वेग की दिशा सदा BC की और तथा C के वेग की दिशा सदा CA की और रहती है । किस समय सभी कण एक-दूसरे से मिलेंगे ?
हल पहली विधि
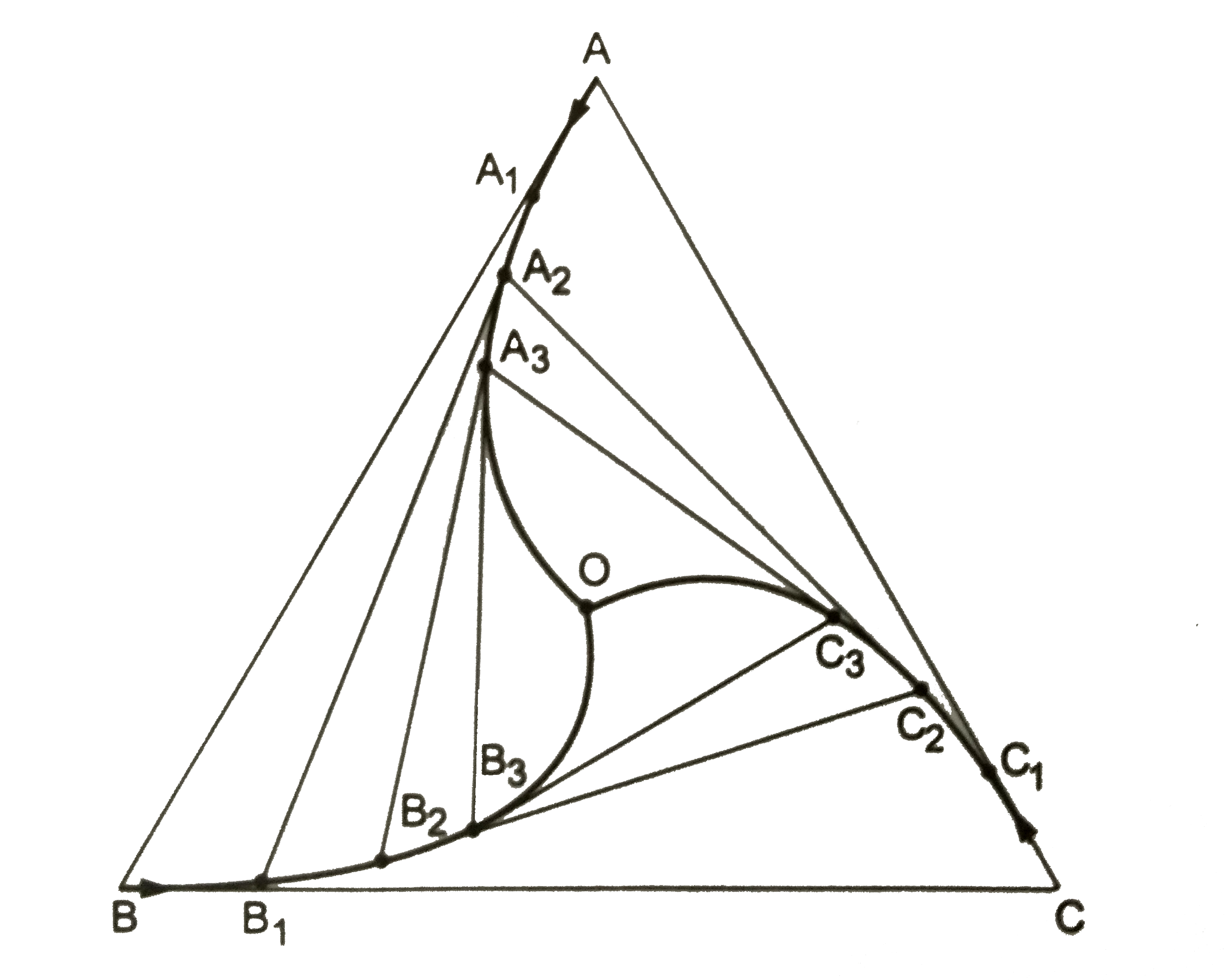
चित्र में A , B , C के चलने के रस्ते दिखाएँ गए है । किसी भी समय तीनो कण एक समबाहु त्रिभुज ही बनाते है जिसका केन्द्रक O हमेशा वही रहता है । तीनो कण सी केन्द्रक O पर ही मिलेंगे जो तीनो कणो के बराबर दुरी पर है ।
चूँकि O समबाहु त्रिभुज का केन्द्रक है , किसी भी क्षण भुजा AB (अर्थात A1B1या A2B2 आदि ) AO से 30∘का कोण बनाएगी । A
के वेग का AO की और घटक =vcosθ किसी भी क्षण दुरी AO के घटने की दर =vcosθ ।
प्रारंभ में t = 0 पर AO=d√3
अतः , दुरी AO को घटकर शून्य होने में लगा समय
=d√3vcos30∘=2d3v .
दूसरी विधि
किसी भी क्षण A का वेग AB दिशा में v है । उसी क्षण B का योग
BC दिशा में v है , अतः B के वेग का BA दिशा में घटक
=vcos60∘=v2 है । अतः , AB के घटने की दर =v+v2=3v2 है ।
t=0 पर AB = d ,अतः AB को घटकर शून्य होने में लगा समय
=d(3v2)=2d3v
Topper's Solved these Questions
- समतल में गति BOOK - HC VERMA HINDICHAPTER - समतल में गति EXERCISE - अभ्यास
7 Videos
- समतल में गति BOOK - HC VERMA HINDICHAPTER - समतल में गति EXERCISE - विचार हेतु प्रश्न
10 Videos
- सदिश राशियों का गणित BOOK - HC VERMA HINDICHAPTER - सदिश राशियों का गणित EXERCISE - अभ्यास के प्रश्न
16 Videos
- सरल आवर्त गति BOOK - HC VERMA HINDICHAPTER - सरल आवर्त गति EXERCISE - अभ्यास के प्रश्न
31 Videos
Similar Questions
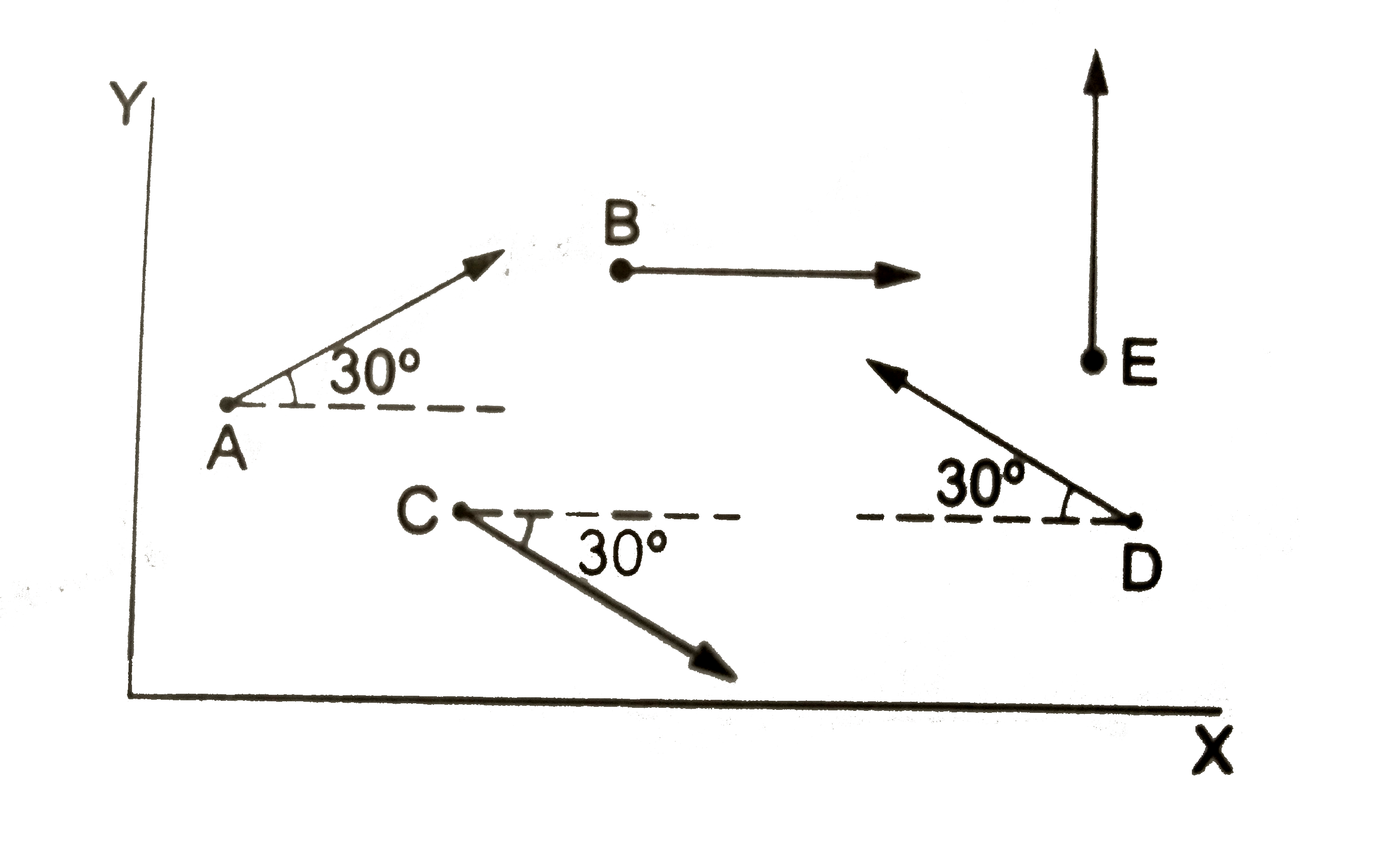
दिए गए चित्र में कुछ कणो के वेग दिखाए गए है । प्रत्येक कण 6 m//s की चाल से चल रहा है । प्रत्येक कण के वेग के x - तथा y-घटक बताएँ ।
View Solutionएक कण का वेग किसी क्षण पश्चिम दिशा की ओर है । इसका त्वरण शून्य नहीं है वह न तो पश्चिम , न ही पूर्व , न ही उत्तर ओर न ही दक्षिण दिशा में है । ऐसी गति का एक उदाहरण दे ।
View Solutionएक वेक्टर →A x -अक्ष से 45∘ का कौन बनाता है ओर उसी ओर घूमते हुए दूसरा वेक्टर →B x -अक्ष से 135∘ का कौन बनता है। इन वेक्टरो के परिमाण क्रमशः 4 इकाई ओर 4 इकाई है।→A तथा →B का परिणामी निकाले।
View Solutionमूलबिंदु को मध्यबिंदु बनाकर -अक्ष पर सरल आवर्त गति करते एक कण का आयाम 10cm तथा आवर्तकाल 6s है।t=0 समय पर इसकी स्थिति =5cm है तथा यह अक्ष की धनात्मक दिशा में चल रहा है। t समय पर इसके विस्थापन के लए समीकरण लिखे।t = 4s समय पर कण के त्वरण का परिमाण निकालें
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
View Solutionध्वनि के वेग की ताप पर निर्भरता
View SolutionA boat takes half time in moving a certain distance downstream than upstream. The ratio of the speed of the boat in still water and that current is एक नाव की किसी निश्चित दूरी को धारा के विपरीत दिशा में जाने मे लगे समय की अपेक्षा धारा के दिशा मे जाने में आधा समय लगता है। शांत जल मे नाव और धारा की गति का अनुपात क्या है?
View Solutionएक व्यक्ति पश्चिम दिशा की ओर मूँह करके खड़ा है | वह दक्षिणावर्त दिशा में 45∘ के कोण पर घूमता है फिर वह पुनः उसी दिशा में 180∘ के कोण पर घूमता है और फिर वह वामावर्त दिशा में 270∘ के कोण पर घूमता है | अब वह किस दिशा की ओर खड़ा है ?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View Solutionदुरी ,वेग ,त्वरण और समय पर ग्राफ
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solutionअभिक्रिया a+bhArrc+d के लिए प्रार में a और b की सांद्रताएं समान होती है। और साम्यावस्था पर d की सांद्रता a की सांद्रता से दोगुनी होती है। अभिक्रिया के लिए साम्य स्थिरांक क्या होगा?
View Solutionसमान विभवांतर के माध्यम से त्वरित हुए alpha कण और प्रोटॉन के लिए तरंग दैर्ध्य के अनुपात की गणना कीजिए।
View Solution
