R त्रिज्या वाला अर्द्धगोलाकार आकार का एक बरतन अपने अक्ष के परितः घुमाया जाता है। यह अक्ष स्वयं एक ऊर्ध्वाधर रेखा पर स्थिर है। बरतन के अंदर एक छोटा गुटका रखा गया है जो उसकी सतह पर बिना फिसले एक जगह बना रहता है। बरतन की सतह घर्षणरहित है और गुटके से होकर जानेवाली त्रिज्या ऊर्ध्वाधर से θ कोण बनाती है। बरतन का कोणीय वेग निकाले।
मान ले कि बरतन का कोणीय वेग ω है। गुटका भी उसी कोणीय वेग से चलता है। गुटके पर लगनेवाले बल है (चित्र 10.W8)
(a) बरतन की सतह द्वारा अभिलंब बल N तथा
(b) गुटके का भार mg.
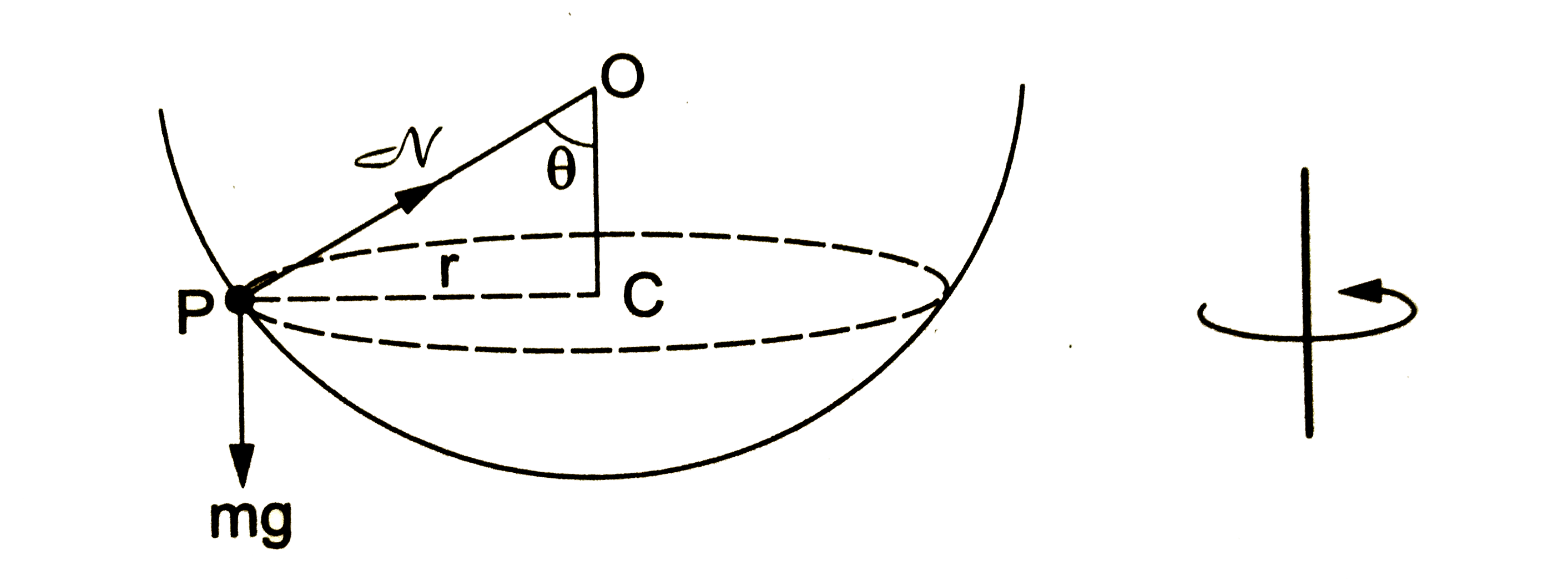
गुटके एक क्षैतिज तल पर वृत्ताकार पथ में चलता है। चित्र से आप देख रहे है कि उस वृत्ताकार पथ की त्रिज्या
r=Rsinθ.
इस पथ की त्रिज्या तथा ऊर्ध्वाधर दिशा में बलों के घटक लेकर न्यूटन के गति-नियम लगाने पर,
Nsinθ=mω2Rsinθ
या N=mω2R तथा Ncosθ=mg.
अतः mω2Rcosθ=mg या ω=√gRcosθ.
यदि हम इस उत्तर में θ=0 रख दे तो ω=√g/R आता है। पर, θ=0 का अर्थ है कि गुटका बरतन के सबसे निचले हिस्से पर पड़ा है। लेकिन, उसे यहाँ पड़ा रखने के लिए तो कोई भी कोणीय वेग नहीं चाहिए। बरतन स्थिर भी पड़ा रहे, तो भी गुटका सबसे नीचे के हिस्से पर बिना फिसले स्थिर पड़ा रह सकता है। पता करे कि हमारा उत्तर θ=0 के लिए क्यों सही नहीं है।
Topper's Solved these Questions
- वृत्त में गति BOOK - HC VERMA HINDICHAPTER - वृत्त में गति EXERCISE - अभ्यास 10.1
1 Videos
- वृत्त में गति BOOK - HC VERMA HINDICHAPTER - वृत्त में गति EXERCISE - अभ्यास 10.2
1 Videos
- लेंस-आधारित उपकरण BOOK - HC VERMA HINDICHAPTER - लेंस-आधारित उपकरण EXERCISE - अभ्यास के प्रश्न
26 Videos
- संवेग- संरक्षण का सिद्धांत, टक्कर BOOK - HC VERMA HINDICHAPTER - संवेग- संरक्षण का सिद्धांत, टक्कर EXERCISE - अभ्यास के प्रश्न
57 Videos
Similar Questions
एक कण 20 cm त्रिज्या वाले वृत्त पर रेखीय वेग 10 m/s से चल रहा है। कण का कोणीय वेग निकाले।
View Solutionएक कण 20 cm त्रिज्या के वृत्त पर चल रहा है। इसकी चाल एकसमान दर से बढ़ती जाती है। यदि चाल 2.0 s में 5.0 m/s से 6.0 m/s हो जाती है, तो कण का कोणीय त्वरण का मान बताएँ।
View Solutionएक मनुष्य खुले स्थान में चार अलग-अलग वृक्षों को देखता है जिनकी ऊँचाइयाँ तथा दूरियाँ नीचे दी गई है। इन वृक्षों को उनकी आभासी ऊँचाइयों के घटते क्रम में लगाएँ।

View Solution1.0 kg तथा 4.0kg द्रव्यमानों के दो कणों की गतिज ऊर्जाएँ बराबर हैं। इनके रैखिक संवेगों का अनुपात ज्ञात कीजिए।
View Solution10 g द्रव्यमान और 50 m/s चाल वाली बंदूक की गोली एक दरवाजे में अंतः स्थापित हो जाती है । दरवाजा 1.0 M चौड़ा है और इसका द्रव्यमान 12 kg है इसके एक सिरे पर कब्जे लगे है और यह इनसे गुजरती एक ऊर्ध्वाधर अक्ष के परितः लगभग बिना घर्षण के घूम सकता है । गोली के दरवाजे में अंतः स्थापन के ठीक बाद इसका कोणीय वेग ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक छड़ की लम्बाई l है । इसका एक सिरा भूमि पर तथा दूसरा सिरा एक ऊर्ध्वाधर दीवार पर टिका है । यदि छड़ भूमि पर फिसले , तो उसके मध्य बिंदु का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक रेखा x- अक्ष से 120∘ तथा y-अक्ष से 60∘ का कोण बनाती है, तो रेखा द्वारा z-अक्ष से बना कोण ज्ञात कीजिए।
View Solutionएक सदिश x- अक्ष v y-अक्ष प्रत्येक के साथ π4 कोण बनाता है, तो z-अक्ष के साथ यह क्या कोण बनाता है ?
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionपरवलय x2=8y पर एक स्पर्श रेखा,जो X-अक्ष की धनात्मक दिशा के साथ कोण θ बनती है, का सभीकरण है
View Solutionयदि एक वक्र बिंदु (1, -2) से होकर जाता है तथा इस पर किसी बिंदु (x, y) पर स्पर्श रेखा का ढाल (slope) x2−2yx है, तो यह वक्र निम्न में से किस बिंदु से होकर जाता है ?
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solution
