m द्रव्यमान वाला एक गुटका अनियमित शक्ल वाले रस्ते पर फिसलता हुआ बिंदु A से चलकर बिंदु B पर पहुँचता है (चित्र 12.6) बिंदु B के सापेक्ष बिंदु A की ऊंचाई h अधिक है यदि वह बिंदु A से फिसलना प्रारम्भ करता है तो बिंदु B पर उसकी चाल निकालें गुटके तथा रस्ते के बीच घर्षण गुणांक को नगण्य माने

गुटके पर लगने वाला बल
(a) गुटके का भार mg तथा
(b) रास्ते द्वारा अभिलम्ब बल
चूँकि वस्तु नीचे आ रही है, अतः mg द्वारा किया गया कार्य = mgh होगा। बल N सदा रास्ते के लंबवत लगेगा और वस्तु के फिसलने की दिशा रास्ते के अनुदिश होगी ये दोनों एक-दूसरे पर लंब होंगे। अतः, किसी भी छोटे अंतराल में N द्वारा किया गया कार्य शून्य होगा और इसलिए पूरे अंतराल में भी यह कार्य शून्य है। इसलिए, गुटके पर किया गया कुल कार्य = mgh.
कार्य-ऊर्जा सिद्धांत से गुटके पर किया गया कुल कार्य उसकी गतिज ऊर्जा में परिवर्तन के बराबर होगा। बिदु A पर गुटके की चाल शून्य है, इसलिए गतिज ऊर्जा भी शुन्य होगी। यदि बिंदु B पर उसकी चाल v हो, तो अंतिम गतिज ऊर्जा होगी। अतः
mgh=12mv2−0 या v=√2gh
Topper's Solved these Questions
- कार्य, शक्ति एवं गतिज ऊर्जा BOOK - HC VERMA HINDICHAPTER - कार्य, शक्ति एवं गतिज ऊर्जा EXERCISE - विचार हेतु प्रश्न
8 Videos
- कार्य, शक्ति एवं गतिज ऊर्जा BOOK - HC VERMA HINDICHAPTER - कार्य, शक्ति एवं गतिज ऊर्जा EXERCISE - सटीक उत्तरवाले प्रश्न I
8 Videos
- कार्य, शक्ति एवं गतिज ऊर्जा BOOK - HC VERMA HINDICHAPTER - कार्य, शक्ति एवं गतिज ऊर्जा EXERCISE - अभ्यास के प्रश्न
32 Videos
- कलन शास्त्र BOOK - HC VERMA HINDICHAPTER - कलन शास्त्र EXERCISE - अभ्यास के प्रश्न
22 Videos
- कोणीय सरल आवर्त गति BOOK - HC VERMA HINDICHAPTER - कोणीय सरल आवर्त गति EXERCISE - अभ्यास के प्रश्न
20 Videos
Similar Questions
क्या स्थितिज घर्षण किसी वस्तु पर धनात्मक कार्य कर सकता है? यदि हा, तो एक उदाहरण दीजिए। यदि नहीं, तो कारण बताइए
View Solutionस्प्रिंग नियतांक k के एक स्प्रिंग के दोनों सिरों से दो समान द्रव्यमान जुड़े हुए है दोनो दव्यमानों को बराबर दूरी खीचकर स्प्रिंग को इसकी मूल लंबाई से कबई तक खीचकर रखा गया है। खीचने के दौरान स्प्रिंग के द्वारा प्रत्येक द्रव्यमान पर किया गया कार्य है
View Solutionएक साईकिलसवार का साइकिलसहित द्रव्यमान 90 kg है। यदि साईकिल की चाल 6 km/h से बढ़कर 12 km/h हो जाए, तो गतिज ऊर्जा में वृद्धि की गणना कीजिए
View Solutionx के निम्नलिखित फलनों के लिए dy/dx निकालें|
(a)x2sinx (b)(2x+3)2 (c)e2x (d)exx
View Solutionजिस दोलक का आवर्तकाल 2 सेकण्ड हो, तो उसे सेकण्ड दोलक कहते हैं। पहले के ज़माने में बहुत -सी घड़ियाँ इसी प्रकार के दोलकों से बनती थी। यदि g का मान π2m/s2 हो, तो सेकण्ड दोलक को लम्बाई निकालें।
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionजब मूलबिंदु (−3,2) पर है तब इस मूलबिंदु के सापेक्ष किसी बिंदु P के निर्देशांक (−3,4) है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक है । बिंदु (0,0) पर मूलबिंदु होने पर इसके निर्देशांक ज्ञात कीजिए
View Solutionबिंदु A(−2,−4)से होकर जाने वाली रेखा X-अक्ष के साथ45∘ का कोण बनाती है तथा रेखा x+3y=8 को बिंदु P पर काटती है AP, के बीच कि दूरी ज्ञात कीजिए ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
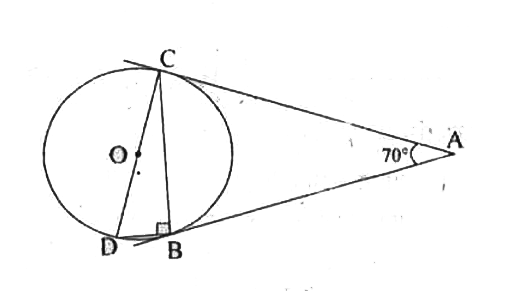
View Solutionदी गई आकृति में बिंदु B ,C तथा D से गुजरने वाले वृत्त के बिंदु B तथा C पर AB तथा AC स्पर्श रेखाएं है। यदि ∠BAC=70∘ और ∠CBD=90∘ तो ∠BCD का मान है -
View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
View Solutionउस बिंदु P का बिन्दुपथ ज्ञात कीजिए जो इस प्रकार गमन करता है कि बिंदु A(am,0),m≠1 से उसकी दूरी , बिंदु B(am,0) से उसकी दूरी की m गुनी रहती है ।
View Solutionमाना कि परवलय x2=8y का शीर्ष O तथा उस पर बिंदु Q है। यदि बिंदु P रेखाखण्ड OQ को 1:3 के आन्तरिक अनुपात में विभाजित करता है, तो P का बिन्दुपथ है :
View Solutionयदि बिंदु (4,6) से होकर जाने वाले मानक अतिपरवलय की उत्केंद्रता 2 है, तो (4,6) पर अतिपरवलय पर खींची गई स्पर्श रेखा का समीकरण है
View Solution
