R0 त्रिज्या के एक खाली बीकर को पानी के टब में इस प्रकार रखा गया हैं कि बीकर के अंदर पानी न जाए । बीकर के व्यास के अनुदिश पानी में चलते हुए प्रकाश का एक पतला पुंज बीकर की दीवार पर पड़ता हैं । दिखाएँ कि बीकर एक अवतल लेंस की भाँति काम करता हैं । यदि इसे बीकर के केंद्र पर रखे एक अवतल लेंस के तुल्य माना जाए , तो इसकी तुल्य फोकस - दूरी निकालें । पानी का अपवर्तनांक = 43 .
चित्र में बीकर का अनुप्रस्थ परिच्छेद ( cross section ) दिखाया गया हैं , जिसससे प्रकाशपुंज आ रहा हैं ।

प्रकाशपुंज पानी से चलकर हवा में प्रवेश करता हैं । बीकर की दीवार पतली होने के कारण इसके व्दारा प्रकाश की किरणों में किसी प्रकार के विस्थापन या विचलन को नगण्य माना जा सकता हैं । इस अपवर्तन के लिए ,
u = ∞,R0,n1=43,n2=1 .
अब सूत्र n2v−n1u=n2−n1R से
1v−43∞=1−43R0
या v=−3R0.
अतः , प्रथम प्रतिबिंब बीकर की बायी सतह से 3R0 पीछे बनेगा । बीकर की दूसरी सतह पर पड़ती किरणों के लिए यही प्रतिबिंब वस्तु हैं । इस सतह पर अपवर्तन के लिए ,
u=−3R0+(−2R0)=−5R0,
R = −R0,n1=1,n2=43.
पुनः सूत्र n2v−n1u=n2−n1R से ,
43v−1−5R0=43−1−R0
या v=−52R0.
अंतिम प्रतिबिंब I इस सतह से 52R0 पीछे बनेगा । बीकर के केंद्र से यह प्रतिबिंब 32R0 पीछे बनेगा । यदि यहाँ एक अवतल लेंस की कल्पना की जाए जो अंतिम प्रतिबिंब I पर ही बनाए , तो उसकी फोकस - दूरी 32R0 होनी चाहिए ।
Topper's Solved these Questions
- गोलीय सतहों पर अपवर्तन BOOK - HC VERMA HINDICHAPTER - गोलीय सतहों पर अपवर्तन EXERCISE - अभ्यास
5 Videos
- गोलीय सतहों पर अपवर्तन BOOK - HC VERMA HINDICHAPTER - गोलीय सतहों पर अपवर्तन EXERCISE - विचार हेतु प्रश्न
6 Videos
- गुरुत्वाकर्षण BOOK - HC VERMA HINDICHAPTER - गुरुत्वाकर्षण EXERCISE - अभ्यास के प्रश्न
40 Videos
- घर्षण BOOK - HC VERMA HINDICHAPTER - घर्षण EXERCISE - अभ्यास के प्रश्न
30 Videos
Similar Questions
चित्र में दिखाई गई परिस्थिति में वस्तु O के प्रतिबिंब का स्थान निर्धारित करें । बिंदु C दोनों माध्यमों की उभयनिष्ठ (COMMON) गोलीय सतह का वक्रता - केंद्र हैं ।
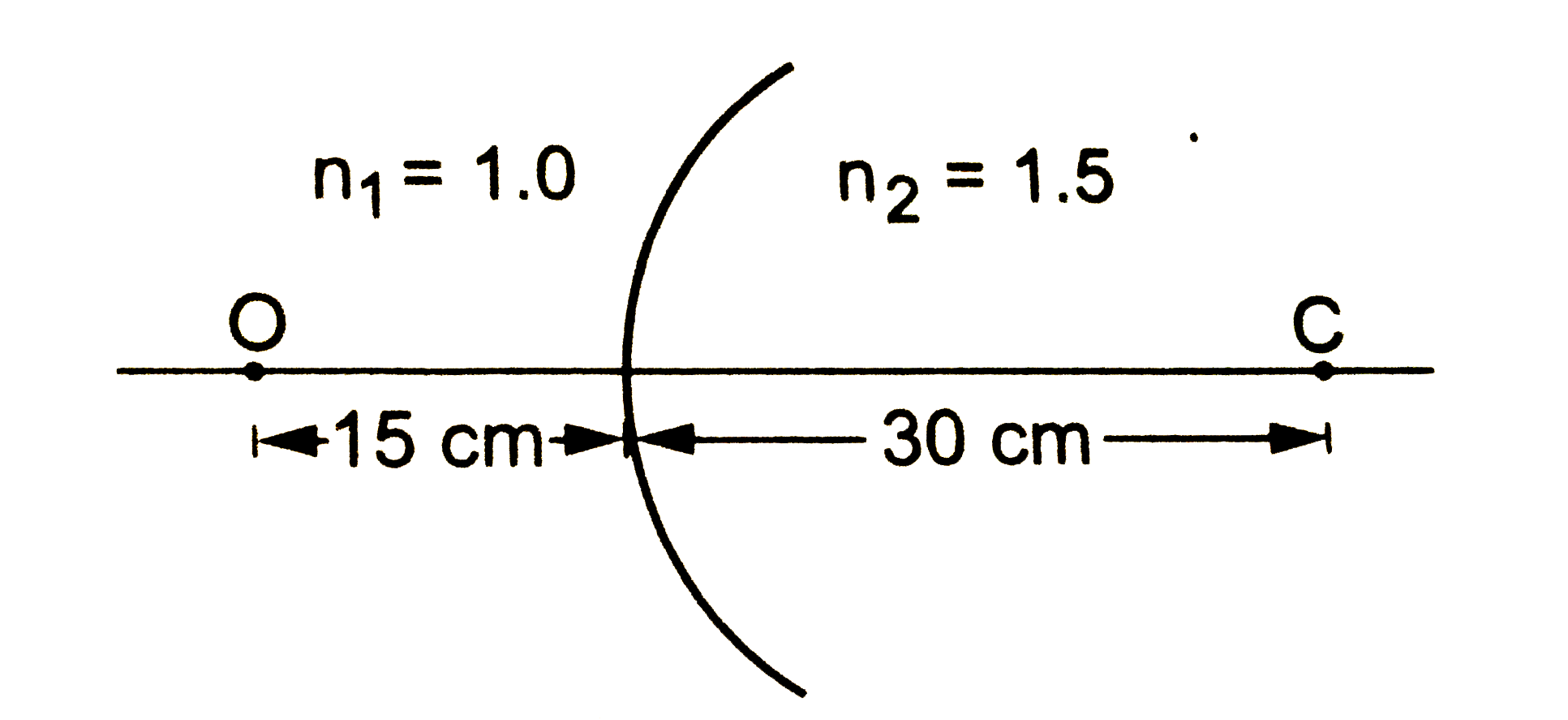
View Solutionएक अपारदर्शी टयूब के अंदर एक लेंस फिट किया हुआ हैं , प्रकाश की एक समानांतर बीम ट्यूब में प्रवेश करती हैं और अपसारी ( divergent) बीम के रुप में ट्यूब के अंदर का लेंस हैं ?
View Solution10 kg द्रव्यमान की दो गोलाकार गेदे एक – दूसरे से 10 cm दूर रखी गई है। इनके बीच लगनेवाले गुरूत्वीय बल ज्ञात करें।
View Solutionएक खुरदरे (rough ) क्षैतिज तल पर फिसल रही वस्तु 4.0m/s2 अवमंदन से गतिशील है|वस्तु तथा तल के बीच गतिज घर्षण गुणांक का मान निकालें|
View Solutionपारे, साबुन के घोल तथा पानी के पृष्ठ-तनाव क्रमश: 0.465N/m,0.03N/m" तथा "0.076 N//m है | निम्नलिखित के लिए बाहर के दाब की अपेक्षा अंदर का अतिरिक्त दाब निकालें-
(a) पारे की 2 mm त्रिज्या की एक बूँद
(b) 4 mm त्रिज्या का साबुन का एक बुलबुला
(c) पानी के एक टैंक में 4 mm त्रिज्या का हवा का एक बुलबुला
View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,5), (6,3) और (5,10)
View Solutionअवतल लेंस के किरण आरेख बनाने के नियम
View Solutionअवतल लेंस के किरण आरेख बनाने के नियम
View Solution“बिहारी के दोहे' के आधार पर लिखिए कि गोपियाँ श्रीकृष्ण की बाँसुरी क्यों छिपा लेती हैं ?
View Solutionअपने विद्यालय में पीने के स्वच्छ पानी की समुचित व्यवस्था हेतु प्रधानाचार्य को एक पत्र लिखिए।
View Solutionलेंस|लेंस के प्रकार|उत्तल लेंस|अवतल लेंस|लेंस के कुछ मुख्य भाग|OMR|Summary
View Solutionज्योतिबा फुले के रचनाकार सुधा अरोड़ा मूलतः एक पर हैं।
View Solutionनए की जन्म कुण्डली : एक पाठ के रचनाकार कौन हैं ?
View Solutionअवतल लेंस के द्वारा प्रतिबिंब का निर्माण
View Solution1 atm के बाह्य दाब के अंतर्गत गतिशील पिस्टन वाले एक निर्वातित पात्र में, He के 0.1 मोल और एक अज्ञात यौगिक के 1.0 मोल (0°C पर 0.68 atm वाष्प दाब) को रखा जाता है। आदर्श गैस व्यवहार मानते हुए, 0°C पर साम्यावस्था पर गैस का कुल आयतन (L में) लगभग x L के समान है। x के मान की गणना कीजिए।
View Solutionएक बंद पात्र में दो बीकर A और B उपस्थित हैं। बीकर A में यूरिया का 152 .4 g जलीय विलयन है, जिसमें 12 g यूरिया है। बीकर B में 196.2 g ग्लूकोस विलयन है, जिसमें 18 g ग्लूकोस है। दोनों विलयनों को साम्यावस्था प्राप्त करने के लिए रख दिया जाता है। साम्यावस्था पर ग्लूकोस विलयन में ग्लूकोस का भार % ज्ञात कीजिए:
View Solution
