एक तिर्यक रेखा के द्वारा दो समान्तर रेखाएं प्रतिच्छेद होती हैं | तो सिद्ध कीजिए कि दो युग्मों के समअर्द्धकों अन्त : कोण, एक आयत से घिरे हैं |
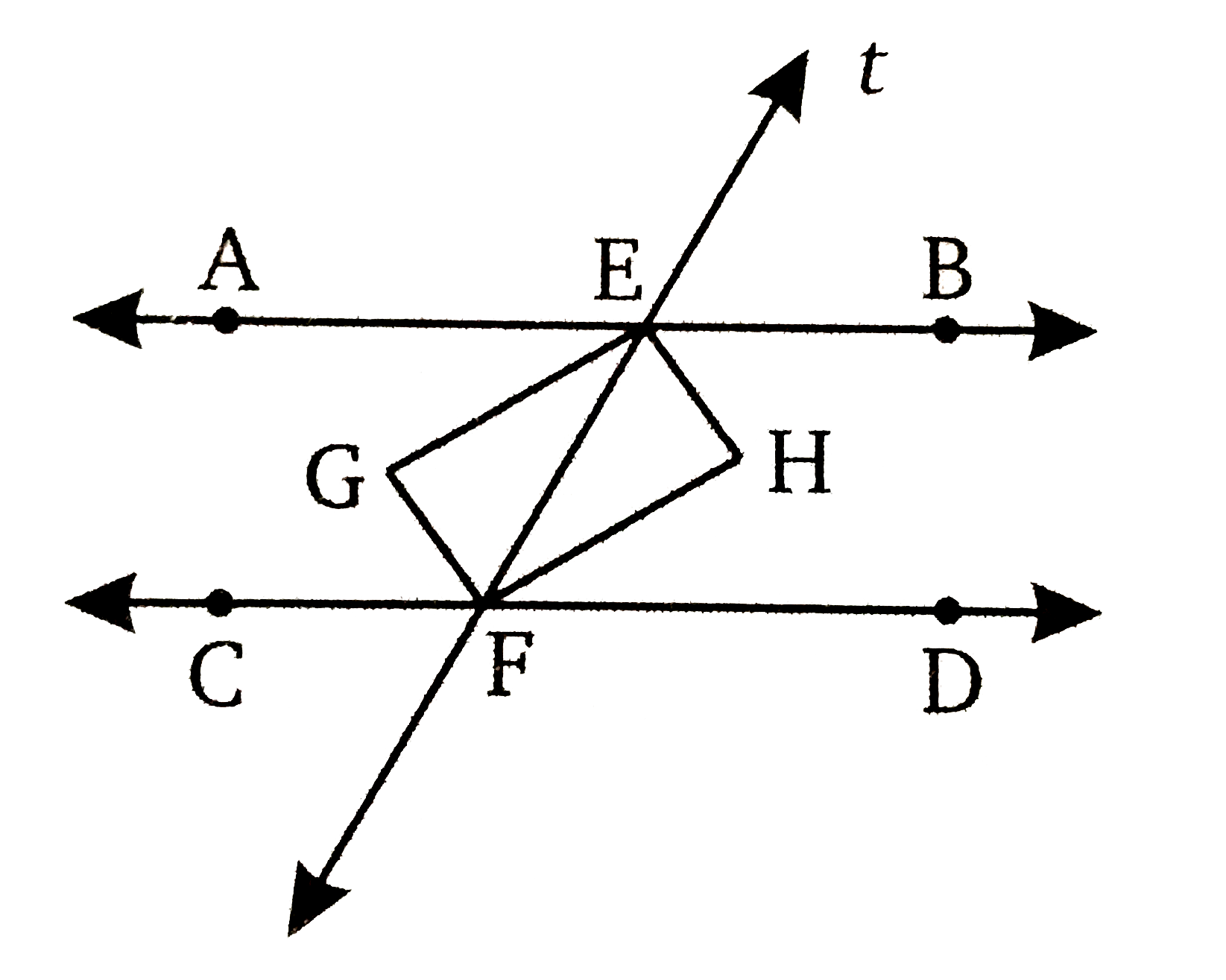
दिया है : AB∣∣CD तथा एक तिर्यक रेखा t इन्हें क्रमश : E तथा F पर काटती है | EG, FG, EH और FH क्रमश : अन्त : कोण ∠AEF,∠CFE,∠BEF और ∠EFD के समअर्द्धक हैं |
सिद्ध करना है : EGFH एक आयत है |
उपपत्ति : AB∣∣CD तथा तिर्यक t इन्हें क्रमश : E और F पर प्रतिच्छेद करती है |
⇒ ∠AEF=∠EFD (एकांतर अन्त: कोण)
⇒ 12(∠AEF)=12(∠EFD) ⇒ ∠GEF=∠EFH
किन्तु ये एकांतर अन्त : कोण हैं | जब तिर्यक EF, EG और FH को प्रतिच्छेद करती हैं |
⇒ EG∣∣∣∣FH इसी प्रकार EH∣∣∣∣GF
∴ EGFH एक समान्तर चतुर्भुज है |
अब यहाँ किरण EF, रेखा AB पर है |
∴ ∠AEF+∠BEF=180∘ (रैखिक युग्म)
12(∠AEF)+12(∠BEF)=90∘
⇒ ∠GEF+∠HEF=90∘ ⇒ ∠GEH=90∘
इस प्रकार समान्तर चतुर्भुज EGFH, में एक कोण समकोण है |
∴ EGFH एक आयत है |
Topper's Solved these Questions
- रेखाएँ एवं कोण BOOK - BALAJI PUBLICATIONCHAPTER - रेखाएँ एवं कोण EXERCISE - विविध उदाहरण
31 Videos
- रेखाएँ एवं कोण BOOK - BALAJI PUBLICATIONCHAPTER - रेखाएँ एवं कोण EXERCISE - अभ्यास प्रश्न 10.1 (अतिलघु उत्तरीय प्रश्न)
6 Videos
- घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन BOOK - BALAJI PUBLICATIONCHAPTER - घन, घनाभ तथा लंबवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन EXERCISE - स्वमूल्यांकन परीक्षण
11 Videos
Similar Questions
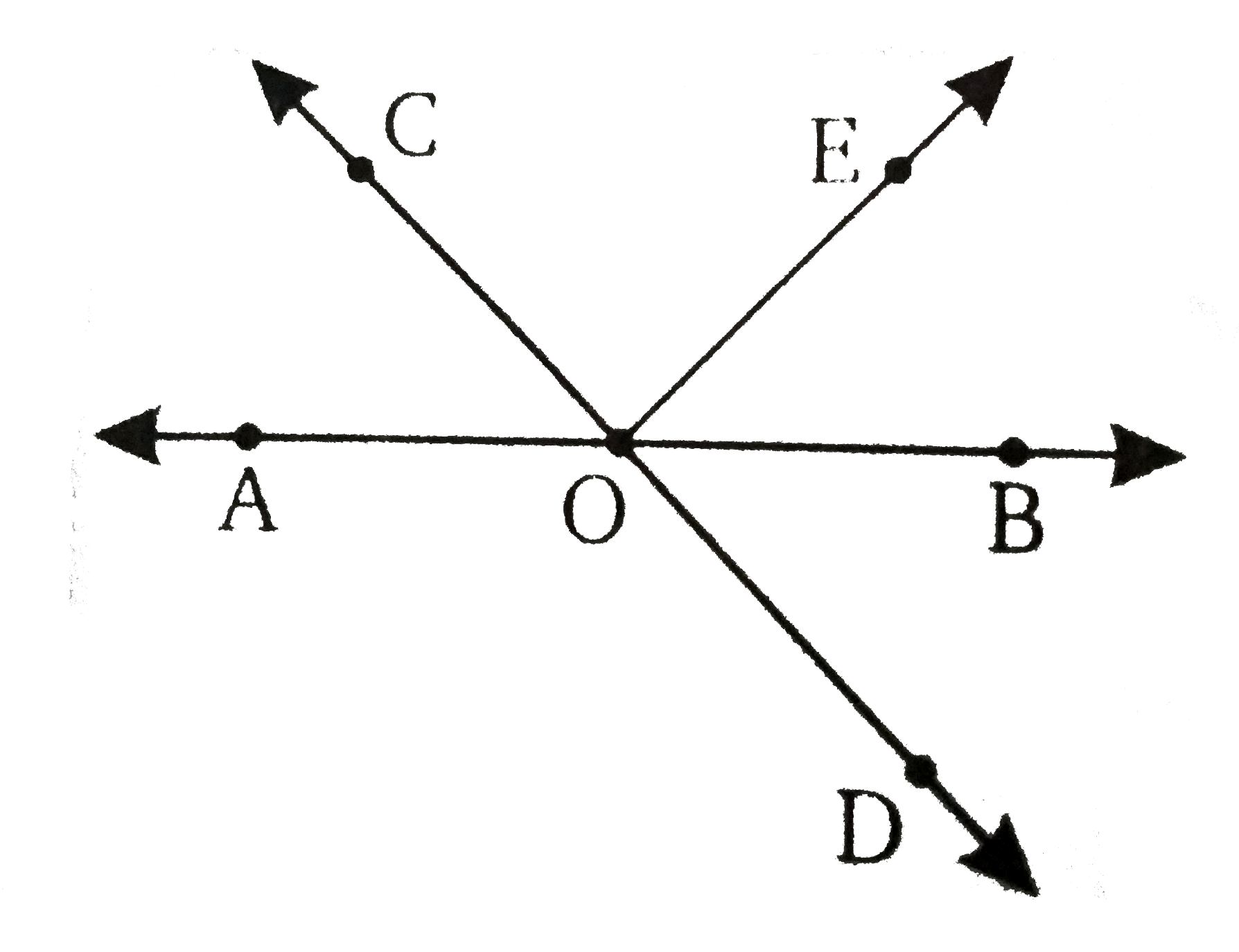
चित्र में रेखाएँ AB और CD, O पर प्रतिच्छेद करती है | यदि ∠AOC+∠BOE=70∘ तथा ∠BOD=40∘, तो ∠BOE और प्रतिवर्ती ∠COE ज्ञात कीजिए |
View Solutionयदि दो पूरक कोणों के बीच का अनुपात 2 : 3 है | तब कोण ज्ञात कीजिए |
View Solutionमंजू अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक आयताकार बॉक्स पर रखना चाहती है । जिसे सांताक्लॉज के चित्र के साथ एक रंगीन कागज़ से ढाका जाना है। उसका यह जानना आवश्यक है कि उसे कितना कागज़ खरीदना चाहिए यदि उपरोक्त बॉक्स की लम्बाई, चौड़ाई एवं ऊचाई 80 सेमी, 40 सेमी, 20 सेमी है तो उसे 40 सेमी भुजा वाली कागज़ की कितनी शीटों की आवश्यकता है।
View Solutionसिद्ध कीजिए कि किसी समचतुष्फलक कि कोई दो सम्मुख कोरें परस्पर लम्ब होती हैं |
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View Solutionदो वृत्त 2.5 सेमी एवं 1 सेमी त्रिजियो के केंद्र परस्पर 7 सेमी दूरी पर है। एक उभयनिष्ठ तिर्यक स्पर्श रेखा कि रचना कीजिए।
View Solutionएक रेखा x- अक्ष से 120∘ तथा y-अक्ष से 60∘ का कोण बनाती है, तो रेखा द्वारा z-अक्ष से बना कोण ज्ञात कीजिए।
View Solutionयदि एक कण पर क्रिया करते हुए तीन बल संतुलन में हैं। पहले दो के बीच का कोण 90∘, ... दूसरे और तीसरे के बीच का कोण 120∘ हैं, तो बलों का अनुपात ज्ञात कीजिए।
View Solutionशृंगार' रस के कौन-से दो भेद हैं।
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solutionदो समतलीय का सह-तलीय होना|दो समतलों के बीच कोण#!#समतल से दिए गए बिंदु की दूरी#!#एक रेखा एवं एक समतल के बीच कोण#!#उदाहरण
View SolutionRevision|समान्तर रेखा और तिर्यक रेखा#!#त्रिभुज के कोण योग का गुण#!#Quiz की सहायता से Revision#!#महत्वपूर्ण प्रश्न
View Solutionएक बिन्दु की रेखा से लम्बवत दूरी |दो समांतर रेखाओ के मध्य दूरी
View Solutionदो रेखाओ के मध्य कोण |बिन्दु से रेखा पर लंब
View Solutionएक रेखा की दिक्-कोसाइन ज्ञात कीजिए तो निर्देशांक्षो के साथ समान कोण बनाती है |
View Solution
