यदि दो समान्तर रेखाएँ एक निर्यक द्वारा प्रतिच्छेद होती है तो सिद्ध कीजिए कि दो युग्मों के अन्तः कोणों के समद्विभाजक द्वारा घिरी आकृति एक आयत है ।
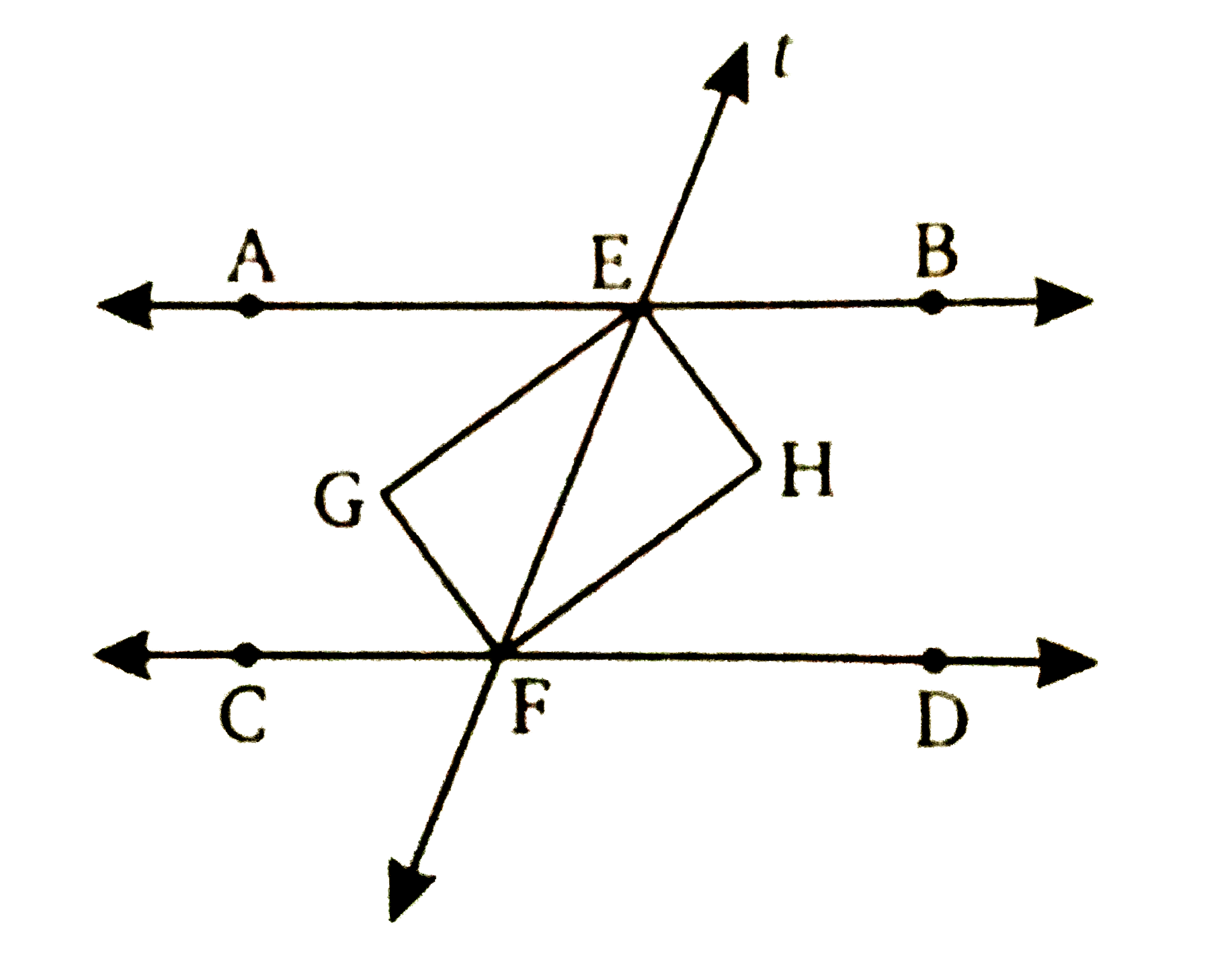
माना दो समान्तर रेखाएँ AB और CD हैं तथा निर्यक t, AB और CD को बिंदु E तथा F पर प्रतिच्छेद करती है ।
माना EF,FG,EH तथा FH अन्तः कोणों के समद्विभाजक हैं।
(अन्तः कोण )
में,
इसी प्रकार ,
पुनः
इसी प्रकार ,
GFHE के सभी कोण समकोण हैं। अतः GFHE एक आयत है ।
Topper's Solved these Questions
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - अभ्यास प्रश्न 11.1(अतिलघु उत्तरीय प्रश्न )
7 Videos
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - अभ्यास प्रश्न 11.1 (लघु उत्तरीय प्रश्न )
13 Videos
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - स्वमूल्यांकन परिक्षण
29 Videos
- त्रिभुजों की सर्वांगसमता BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
Similar Questions
यदि एक त्रिभुज के दो कोण बराबर है तब दोनों की विपरीत भुजा बराबर है या नहीं ?
View Solutionएक त्रिभुज के कोण 2:3:7 के कोण में है । त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
View Solutionसिद्ध कीजिए की एक समान्तर चतुर्भुर्ज की विपरीत के मध्य बिंदुओं को मिलाने वाली सरल रेखा, समान्तर भुजाओं के अन्य युग्म से समान्तर होती है।
View Solutionरेखा l कोण A की समद्विभाजक है तथा l पर कोई बिंदु B है| BP और BQ बिंदु B से ∠Aकी भुजाओं पर लम्ब है तो दिखाइये कि-

(i) ΔAPB≅ΔAQB
(ii) BP=BQ
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionएक सरल रेखा द्वारा अक्षो के बीच काटे गये अन्तः खण्ड को बिंदु (7,9),3:1 के अनुपात में अन्तः विभाजित करता है रेखा का समीकरण ज्ञात कीजिए
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionदो वृत्त एक -दूसरे को अन्तः स्पर्श करते है ,तो उनकी उभयनिष्ठ स्पर्श रेखाओ कि संख्या लिखिए।
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक दंपत्ति के दो बच्चे है। प्रायिकता ज्ञात कीजिए
दोनों बच्चें लड़कियाँ है , यदि यह ज्ञात है कि बड़ा बच्चा लड़का है।
View Solutionयदि शब्द PROBABILITY के अक्षर एक पंक्ति में यदृच्छया लिखे जाते है तो दो के साथ आने की प्रायिकता है -
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solution
