(a) निम्न चित्र में एक लंबा सीधा वृत्ताकार अनुप्रस्थ काट (जिसकी त्रिज्या a है) विधुत धारावाही तार जिससे स्थायी विधुत धारा I प्रवाहित हो रही हो दर्शाया गया है स्थायी विधुत धारा इस अनुप्रस्थ काट पर एकसमान रूप से वितरित है क्षेत्रो r<a तथा r>a में चुम्बकीय क्षेत्र परिकलित कीजिए जहाँ r तार के केंद्र से किसी बिंदु P की दूरी है ।

(b) तार के पृष्ठ a2 से ऊपर बिंदु पर तथा तार के पृष्ठ के नीचे a2 बिंदु पर चुम्बकीय क्षेत्र का अनुपात ज्ञात कीजिए ।
इस तार हेतु के अधिकतम मान की गणना कीजिए ।
(a) (i) प्रथम स्थिति में माना r>a
ऐम्पियर पाश 2 : तार के अनुप्रस्थ परिच्छेद के संकेन्द्री वृत्त है |
अतः इस पाश के लिए L=2πr और पाश में प्रवाहित धारा I है |
अतः ऐम्पियर के परिपथीय नियम से,
BL=μ0I,
या B.2πr=μ0I
या B=μ0I2πr, [∵r>a]
या B∝1r
जब r<a तब बंद पाश 1 (ऐम्पियर पाश) से
L=2πr
लूप 1 से प्रवाहित धारा <I तब धारा वितरण एकसमान तब पाश 1 से प्रवाहित धारा I1=Iπa2πr2
या I1=Ir2a2
या B.2πr=μ0Ir2a2
या B=μ0I2πa2⋅r [r<a]
अतः B∝r
जहाँ r, तार के केंद्र से बिंदु P की दूरी है
अर्थात चुम्बकीय क्षेत्र B,r के समानुपाती है अर्थात जब हम अर्थात चुंबकीय क्षेत्र के समानुपाती है अर्थात जब हम बेलन के अक्ष से उनसके पृष्ठ की किसी बिंदु की ओर आते है तब चुम्बकीय क्षेत्र की तीव्रता 1r के अनुसार परिवर्तित होने लगती है चुम्बकीय क्षेत्र के मान में r के सापेक्ष परिवर्तन निम्न ग्राफ में प्रदर्शित है
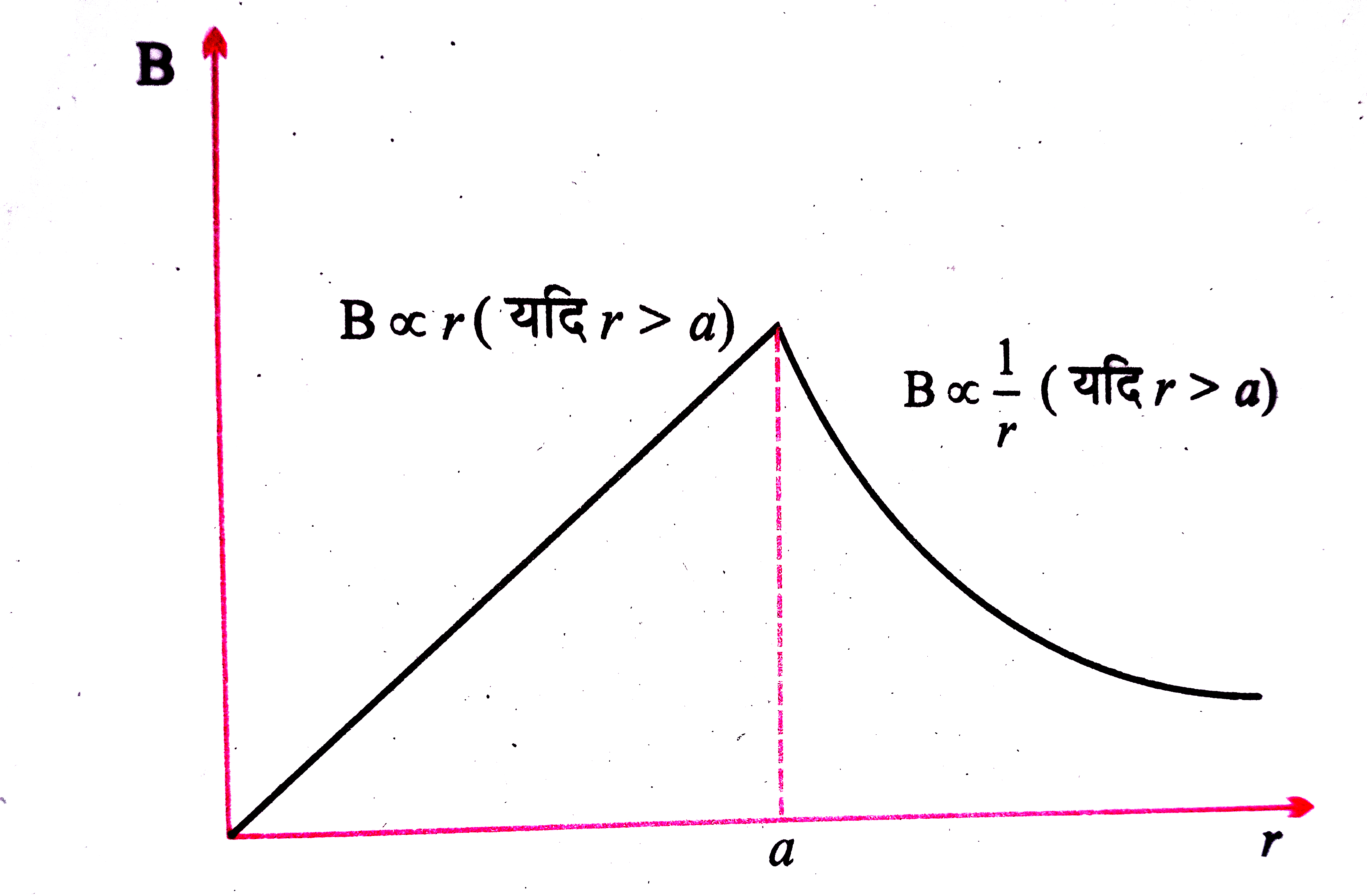
(b) माना कोई बिंदु P तार से a2 दूरी ऊपर तथा अन्य बिंदु Q,a2 दूरी नीचे स्थित है अतः B=μ0I2πr.
यदि r=3aa (तार के अक्ष से दूरी) पर चुंबकीय क्षेत्र
BP=μ0I2π(3a2)=μ0I2πa
तार के अक्ष से r=a2 दूरी पर स्थित बिंदु Q चुंबकीय क्षेत्र
BQ=μ0Ir2πa2
यदि r=a2 तब BQ=μ0I2πa2=a2=μ0I4πa
∴ BPBQ=μ0I/3πaμ0I/4πa=43
BPBQ=43
अतः तार के पृष्ठ पर B का मान अधिकतम होगा
अर्थात r=a पर B=Bmax
∴ Bmax=μ0I2πa .
Topper's Solved these Questions
- गतिमान आवेश और चुंबकत्वBOOK - PRABODH PUBLICATIONCHAPTER - गतिमान आवेश और चुंबकत्वEXERCISE - तथ्यात्मक प्रश्न
15 Videos
- गतिमान आवेश और चुंबकत्वBOOK - PRABODH PUBLICATIONCHAPTER - गतिमान आवेश और चुंबकत्वEXERCISE - अभ्यासार्थ प्रश्न (वस्तुनिष्ठ प्रश्न) I. बहुविकल्पीय प्रश्न
10 Videos
- गतिमान आवेश ओर चुम्बकत्व BOOK - PRABODH PUBLICATIONCHAPTER - गतिमान आवेश ओर चुम्बकत्व EXERCISE - आंकिक प्रश्न
12 Videos
- चुम्बकत्व एवं पदार्थों के चुम्बकीय गुणBOOK - PRABODH PUBLICATIONCHAPTER - चुम्बकत्व एवं पदार्थों के चुम्बकीय गुणEXERCISE - मूल्य आधारित प्रश्न
6 Videos
Similar Questions
यदि एक तार में विधुत धारा प्रवाहित की जाए तो कौन-सा क्षेत्र उत्पन्न होगा ?
View Solutionचुम्बकीय क्षेत्र की तीव्रता का C.G.S. मात्रक है -
View Solutionतार की एक वृत्ताकार कुण्डली में 100 फेरे हैं । प्रत्येक की त्रिज्या 8.0 cm है ओर इनमें 0.40 A विद्युत धारा प्रवाहित हो रही है । कुण्डली हो रही है । कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का परिणाम क्या होगा ?
View Solutionएक भौतिक शिक्षक अपनी कक्षा में स्थिर विधुत के गॉस नियम तथा चुम्बकत्व के गॉस नियम को समझाते हैं । उनके अनुसार निर्वात में किसी बंद वक्र के अभिलम्बवत विधुत फ्लक्स हैं , जहाँ बंद पृष्ठ के भीतर उपस्थित कुल आवेश का बीजीय योग है । चुंबकीय क्षेत्र में एकल ध्रुव का अस्तित्व नहीं होता है । चुंबकीय ध्रुव हमेशा दो समान प्रबलता के आसमान ध्रुवों को जोड़ा होता है । उपरोक्त अनुच्छेद को पढ़कर निम्न प्रश्नों के उत्तर दीजिए -
दैनिक जीवन में चुम्बकत्व के गॉस नियम की क्या उपयोगिता है ?
View Solutionएक लम्बे सीधे तार में बहने वाली धारा 1 ऐम्पियर है। चुंबकीय क्षेत्र की तीव्रता 10−5 वेबर/मीटर2 होगी तार से :
View Solutionविधुत धारा |चालक में विधुत धारा | धारा घनत्व
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View SolutionAmpere has given a theory to find the magnetic field due to current distribution. in loop धारा I_(3) के चुम्बकीय क्षेत्र में अंशदान को नहीं लेते है क्योंकि चुम्बकीय क्षेत्र पुरे लूप मे युग्मित है। एक समाक्षीय केबिल में तार की त्रिज्या a है , इसके चारो ओर के बेलनाकार सेल की आंतरिक व बाह्य त्रिज्याएँ क्रमशः b तथा c है। अंदर वाले तार में i ऐम्पियर धारा बहती है तथा बाहरी सेल में बराबर व विपरीत धारा बहती है। अक्ष से x दूरी ( x lt a) पर चुंबकीय क्षेत्र है
View Solutionचुंबकीय क्षेत्र में धारावाही तार
View Solutionसमान रूप से आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता व उस पर आधारित प्रशन
View Solutionआवेश का वितरण कितने प्रकार का होता है #!#रेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता
View Solutionरेखीये आवेशित चालक तार के कारण विधुत क्षेत्र की तीव्रता पर आधारित प्रश्न
View Solutionविधुत विभव व विधुत क्षेत्र की तीव्रता में संबंद #!#विधुत विभव ,विधुत क्षेत्र पर प्रश्न
View Solutionएक समान विधुत क्षेत्र में आवेशित कण की गति #!#वृत्ताकार वलय के कारण विधुत क्षेत्र की तीव्रता
View Solution
