एक चर बिंदु का बिंदुपथ वह पथ होता है जो उस बिंदु द्वारा एक या अधिक प्रतिबंधों को संतुष्ट करता है। बिंदुपथ पथ पर स्थित सभी बिंदुओं का समुच्चय होता है।
एक संबंध f(x,y)=0 जोकि x तथा y के बीच है जो बिंदुपथ पर स्थित सभी बिंदुओं द्वारा संतुष्ट होता है। इस प्रकार है कि संबंध को संतुष्ट करने वाला प्रत्येक बिंदु बिंदुपथ पर हो।
मान लीजिए ΔABC के दो शीर्ष A(2,−3) तथा B(−2,1) है। यदि इस त्रिभुज को केंद्रक रेखा 2x+3y=1 पर स्थित है तब शीर्ष C के बिंदुपथ का समीकरण है
2x+3y=9
2x−3y=7
3x+2y=5
3x−2y=3
The correct Answer is:A
माना त्रिभुज के शीर्ष C के निर्देशांक (x,y) है तथा केंद्रक के निर्देशांक (x1,y1 है।
∴x1=x+2−23⇒x1=x3
तथा y1=y−3+13⇒y1=y−23
∵ केंद्रक (x1,y1) रेखा (2x+3y=1) पर स्थित है।
∴2x1+3y1=1
⇒2(x3)+3(y−23)=1
⇒2x+3y=9
जोकि शीर्ष C के बिंदुपथ का समीकरण है।
Topper's Solved these Questions
- समकोणीय कार्तीय निर्देशांक एवं सरल रेखा Book:NDA PATHFINDERChapter:समकोणीय कार्तीय निर्देशांक एवं सरल रेखा Exercise:अभ्यास प्रश्नावली (विगत वर्षों के प्रश्न)
Explore 65 Videos
- समकोणीय कार्तीय निर्देशांक एवं सरल रेखा Book:NDA PATHFINDERChapter:समकोणीय कार्तीय निर्देशांक एवं सरल रेखा Exercise:अभ्यास प्रश्नावली (विगत वर्षों के प्रश्न)
Explore 65 Videos
- सदिश बीजगणित Book:NDA PATHFINDERChapter:सदिश बीजगणित Exercise:विगत वर्षो के प्रश्न
Explore 60 Videos
- समुच्चय सिद्धान्तBook:NDA PATHFINDERChapter:समुच्चय सिद्धान्तExercise:विगत वर्षो के प्रश्न
Explore 29 Videos
Similar Questions
(0,1) से गुजरने वाली तथा Y-अक्ष से रेखा x−y=4 के X-अक्ष के झुकाव के बराबर कोण बनाने वाली रेखा का समीकरण क्या है?
View Solution(0,1) से गुजरने वाली तथा Y-अक्ष से रेखा x−y=4 के X-अक्ष के झुकाव के बराबर कोण बनाने वाली रेखा का समीकरण क्या है?
View Solutionसदिश −ˆi+12ˆj+4ˆk,ˆi+12ˆj+4ˆk,ˆi−12ˆj+4ˆk एव −ˆi−12ˆj+4ˆk वाले शीर्षो A,B,C तथा D से बने आयत का क्षेत्रफल क्या है
View Solutionयदि A कोई B समुच्चय हो तो A∩(A∪B) किसके बराबर है ?
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionसमतल में लुढ़कने वले वृत्त के केंद्र का बिंदु पथ होता है:
View Solutionसंलग्न आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक - दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा:
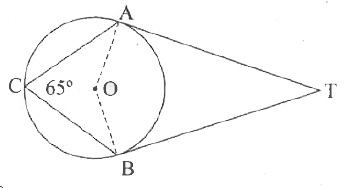
View Solutionसंल्गन आकृति में O वृत्त का केंद्र है तथा AT व BT दो स्पर्श रेखाएं है जो बिंदु पर एक -दूसरे को कटती है। यदि ∠ACB=65∘ हो ,तो ∠ATB का मान होगा -

View Solutionसुसंगत क्षेत्र में बिंदु जो उदेश्य फलन का इष्टतम मान (अधिकतम या न्यूनतम ) एक देता है, वह कहलाता है -
View Solutionनिम्न कथन सत्य है अथवा असत्य-
यदि सुसंगत क्षेत्र के दो कोनीय बिंदुओं पर इष्टतमकारी मान समान हो अर्थात दोनों बिंदुओं के लिए उद्देश्य फलन का मान या तो उच्चतम या निम्नतम हो तब इन बिंदुओं को मिलाने वाली रेखा पर किसी भी बिंदु के लिए उद्देश्य फलन का इष्टतमकारी मान प्राप्त होता है।
View Solutionनिम्न कथन सत्य है अथवा असत्य-
उद्देश्य फलन का अधिकतम मान, परिबद्ध क्षेत्र के किसी एक शीर्ष पर होता है।
View Solutionएक द्विघात बहुपद f(x), जो f(0)=0,f(1)=1,f'(x)>0, को सभी x∈(0,1) के लिए संतुष्ट करता है, है
View Solutionबिंदु (4, 1) किस रेखा के समीकरण को संतुष्ट करता है ?
View Solutionयदि बिंदु (3,4) समीकरण 3y=ax+6 के आलेख पर स्थित है , तो a का मान होगा :
View Solutionएक बिंदु P, x-अक्ष पर और एक अन्य बिंदु Q, y-अक्ष पर स्थित है। (i) बिंदु P की कोटि ज्ञात कीजिए।
View Solution
