सिद्ध कीजिए की अवतल दर्पण के लिए फोकस दूरी =12 वक्रता त्रिज्या ।
वक्रता त्रिज्या - गोलीय दर्पण के ध्रुव और वक्रता केंद्र के बीच की दूरी को उस दर्पण की वक्रता त्रिज्या कहते है ।
फोकस दूरी - गोलीय दर्पण के ध्रुव व मुख्य फोकस के बीच की दूरी को उस दर्पण की फोकस दूरी कहते है ।
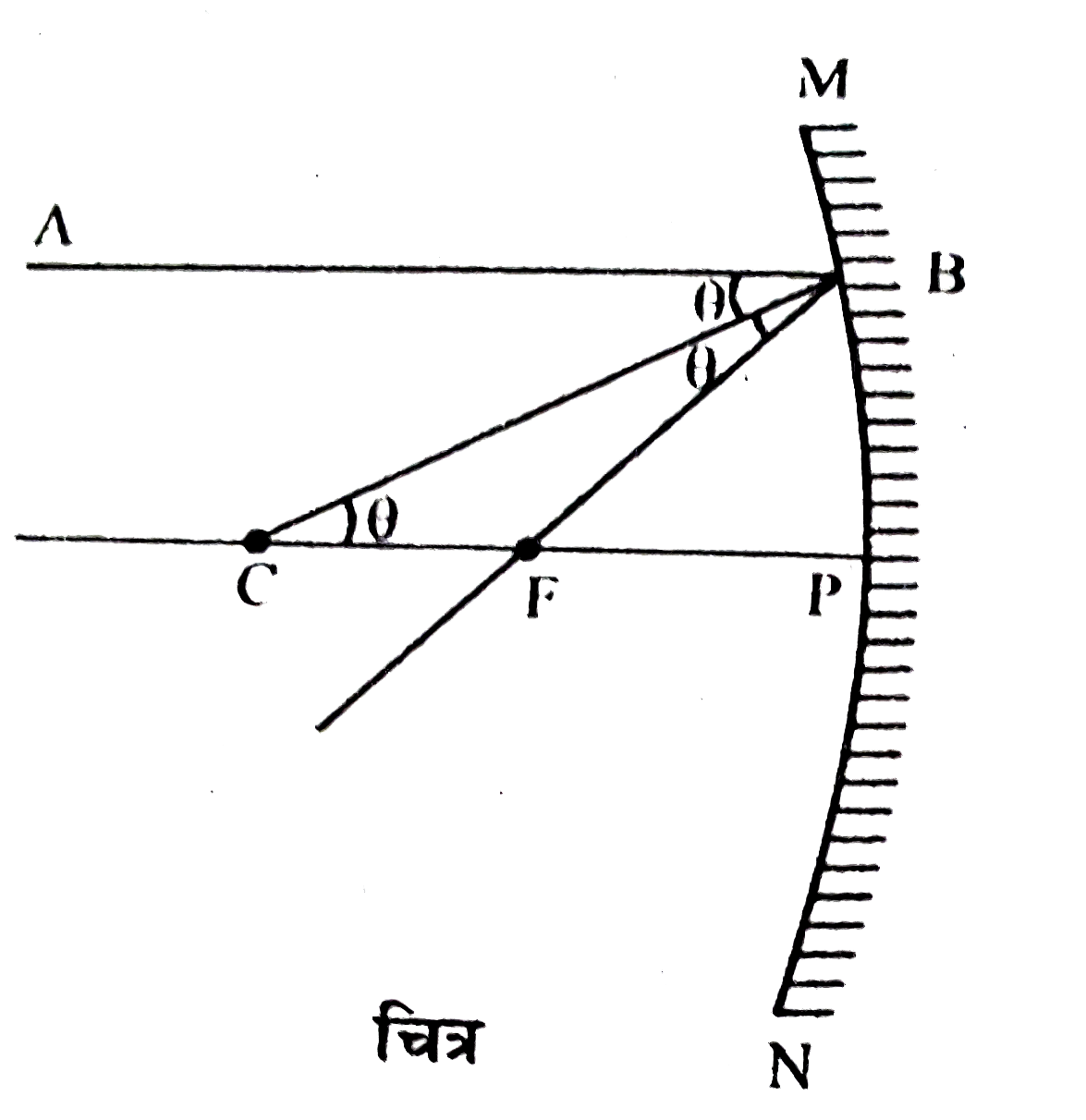
चित्र में MPN एक अवतल दर्पण है । P उसका ध्रुव , F फोकस , C वक्रता केंद्र तथा PC मुख्य अक्ष है ।
एक किरण AB मुख्य अक्ष के समांतर आपतित होती है । यह किरण परावर्तन के पश्चात फोकस F से होकर चली जाती है । CB को मिलाओ । तब CB बिंदु B पर दर्पण का अभिलम्ब होगा ( क्योकि त्रिज्या परिधि के किसी बिंदु पर अभिलंबवर्त होती है ) परावर्तन के नियमानुसार , आपतन कोण ABC =परावर्तन कोण CBF
=θ (मानलो )
AB और PC समांतर है तथा उन्हें BC रेखा मिलती है ,
∴∠ABC=∠BCF=θ
ΔBCF में ,
∠CBF=∠BCF=θ
∴FC=BF
यदि दर्पण का द्वारक छोटा हो , तो BF=PF (लगभग )
∴FC=PF
FC+PF=PF+PF
PC=2PF
R=2f [ because PC =R तथा PF=f]
f=R2 यही अभीस्ट संबंध है
Topper's Solved these Questions
- प्रकाश का परावर्तनBOOK - NAVBODHCHAPTER - प्रकाश का परावर्तनEXERCISE - आंकिक प्रश्न
3 Videos
- प्रकाश का परावर्तनBOOK - NAVBODHCHAPTER - प्रकाश का परावर्तनEXERCISE - लघु उत्तरीय प्रश्न
14 Videos
- परिचय BOOK - NAVBODHCHAPTER - परिचय EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोतर
16 Videos
- प्रकाशिक यंत्र BOOK - NAVBODHCHAPTER - प्रकाशिक यंत्र EXERCISE - NCERT पाठ्यपुस्तक के प्रश्नोत्तर
56 Videos
Similar Questions
अवतल दर्पण के सामने एक वस्तु 48 सेमी की दूरी पर रखी है तथा दर्पण की फोकस दूरी 24 सेमी है । प्रतिबिम्ब की स्थिति एवं प्रकति ज्ञात कीजिये
View Solutionगोलीय दर्पण क्या है ? इसके प्रकार लिखिये।
View Solutionविज्ञानं की प्रकृति से संबंधित कुछ अत्यंत पारंगत प्रकथन आज तक के महानतम वैज्ञानिको में से एक अल्बर्ट आइंस्टाइन द्वारा प्रदान किए गए है। आपके विचार से आइंस्टाइन का उस समय क्या तातपर्य था, जब उन्होंने कहा था " संसार के बारे में सबसे अधिक अबोधगम्य विषय यह है की यह अबोधगम्य है "?
View Solution2.5cm साइज की कोई छोटी मोमबती 36cm वक्रता त्रिज्या के किसी अवतल दर्पण से 27cm दुरी पर रखी है| दर्पण से किसी परदे को कितनी दुरी पर रखा जाए कि उसका सुस्पष्ट प्रतिबिम्ब परदे पर बने| प्रतिबिम्ब कि प्रकृति और साइज का वर्णन कीजिए| यदि मोमबती को दर्पण की ओर ले जाएँ, तो परदे को किस ओर हटाना पड़ेगा?
View Solutionउत्तल दर्पण तथा अवतल दर्पण के उपयोग | महत्वपूर्ण प्रश्न
View Solutionलेंस की फोकस दूरी की निर्भरता|लेंस सूत्र तथा संयुग्मी फोकस
View Solutionसंपर्क में रखे दो पतले लेंसों की संयुक्त फोकस दूरी|उत्तल लेंस तथा समतल दर्पण का संयोजन#!#लेंसों के उपयोग
View Solutionदर्पण द्वारा प्रतिबिम्बों के निर्माण के नियम |अवतल दर्पण
View Solutionअवतल दर्पण के द्वारा विभिन्न स्थितियों पर बिम्ब के लिए प्रतिबिम्ब का निर्माण
View Solutionगोलीय दर्पण के भाग|उत्तल दर्पण तथा अवतल दर्पण द्वारा प्रतिबिम्ब बनने के नियम|OMR|Summary
View Solutionअवतल दर्पण द्वारा प्रतिबिम्ब बनाना|अवतल दर्पण के उपयोग|उत्तल दर्पण द्वारा प्रतिबिम्ब बनाना|उत्तल दर्पण के उपयोग|OMR|Summary
View Solutionअवतल दर्पण के द्वारा प्रतिबिंब बनने के नियम
View Solutionअवतल दर्पण से प्रतिबिंब बनने के नियम
View Solutionअवतल दर्पण के द्वारा विभिन्न स्थितियों पर रखी वस्तुओं के लिए प्रतिबिंब का निर्माण
View Solutionअवतल दर्पण के अनुप्रयोग #!#उत्तल दर्पण से प्रतिबिम्ब निर्माण
View Solutionफोकस दुरी वक्रता त्रिज्या में सम्बन्ध#!#दर्पण सूत्र व उस पर आधारित प्रशन
View Solution
