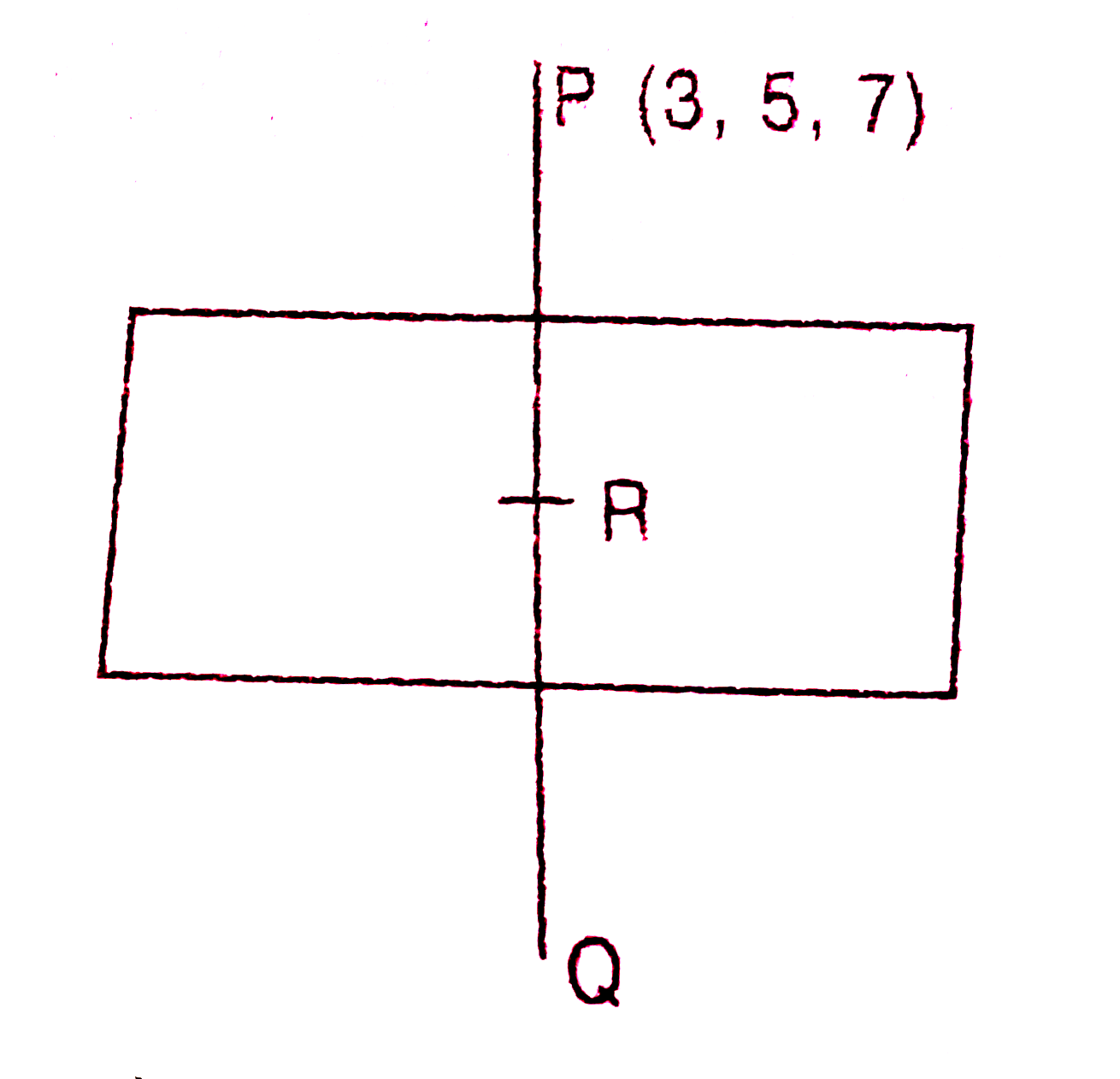
बिंदु P(3,5,7) का हल 2x+y+z=16 में प्रतिबिम्ब ज्ञात करे |
दिया गया तल है, 2x+y+z=16 ...(1)
प्रश्न से , P≡(3,5,7)
तल (1 ) पर लम्ब के दिक् - अनुपात 2, 1 , 1 है |
माना कि तल (1 ) में बिंदु P का प्रतिबिम्ब Q(α,β,γ) है |
तो PQ⊥ तल (1) पर
रेखा PR का समीकरण है x−32=y−51=z−71=r ( माना )
माना कि R≡(2r+3,r+5,r+7)
चूँकि R तल (1 ) पर है,
∴2(2r+3)+r+5+r+7=0
या 6r+18=0∴r=−3∴R≡(−3,2,4)
चूँकि R,PQ का मध्य बिंदु है
∴−3=α+32⇒α=−9 तथा 2=β+52⇒β=−1
4=γ+72⇒γ=1 अतः Q≡(−9,−1,1)
Topper's Solved these Questions
Similar Questions
इन तलों के कार्तीय समीकरण ज्ञात करें जिनके सदिश समीकरण है :
→r⋅(3ˆi+3ˆj−4ˆk)=0
View Solutionएक शंकु की ऊँचाई में वृद्धि 2% है तथा इसका अर्ध शीर्ष कोण अपरिवर्तित है। इसके (i) कुल पृष्ठ क्षेत्रफल (ii) आयतन में
सन्निकट प्रतिशत बढ़ोतरी वृद्धि क्या है?
View SolutionA के बारे में ज्ञात है कि वह 5 में से 3 बार सत्य बोलता है। वह एक पासे को फेंकता है और बतलाता है कि उस पर आनेवाली संख्या 1 है। इसकी प्रायिकता ज्ञात कीजिए कि पासे पर आने वाली संख्या वास्तव में 1 है।
View Solutionबिन्दु (−3,5,2) का समतल 2x−y+z=0 पर प्रतिबिम्ब ज्ञात कीजिए।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionबिंदु (4,−13) का रेखा 5x+y+6=0 पर प्रतिबिम्ब ज्ञात कीजिए
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए , जो रेखाओ x+y=3 तथा 2x+3y=7 के प्रतिच्छेद बिंदु को रेखाओ 2x+3y=8 तथा 3x−y=1 के प्रतिच्छेद बिंदु से मिलती है ।
View Solution(x−2x2)−3 के प्रसार में x7 का गुणांक ज्ञात कीजिए|
View Solution(1−2x+3x2−...............अनंत तक )−7 में x7 का गुणांक ज्ञात कीजिए|
View Solutionसमतल 2x+4y−z=3 तथा रेखा x−12=y−2−3=z+54 का प्रतिच्छेद बिंदु ज्ञात कीजिए।
View Solutionअवकल समीकरण
(2x+4y+3)dydx=x+2y+1
का व्यापक हल ज्ञात कीजिए ।
View Solutionनिम्न समस्या को हल कीजिए :
Z=6x−2y का अधिकतम मान ज्ञात कीजिए जबकि
2x−y≤2,x≤3,x≥0,y≥0
View Solutionरेखा x−42=y−52=z−31 तथा समतल x+y+z=2 का प्रतिच्छेदन बिंदु निम्न में से किस रेखा पर स्थित है ?
View Solutionसीखें कैसे करे 5 अंक वाले प्रश्नो को हल | मानव का तंत्रिका तंत्र
View Solutionबिन्दु (1,8,4) का समतल 2x -y+z+8= 0 में प्रतिबिम्ब बिंदु होगा
View Solutionकिस अनुपात में बिंदु (−25,a) बिंदुओं (-4,3) और (2,8) को विभाजित करता है ? a का मान ज्ञात कीजिए।
View Solution