यदि एक रेखा पर स्थित दो बिंदुओं A और B के बीच एक बिंदु C ऐसा स्थित है कि AC = BC हैं , तो सिद्ध कीजिए कि AC=12AB हैं । एक आकृत्ति खींचकर इसे स्पष्ट कीजिए ।
माना कि AB एक रेखाखंड हैं और A और B के बीच इसपर C एक ऐसा बिंदु हैं कि AC = BC

प्रमाण : अब AC + AC = BC + AC [ ∵ AC = BC ]
इसलिए 2AC = AB [ BC + AC, AB के संपाती हैं ]
अतः AC=12AB
Topper's Solved these Questions
- यूक्लिड की ज्यामितीय का परिचय BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - अभ्यास 7.1 (अतिलघु उत्तरीय प्रश्न )
5 Videos
- यूक्लिड की ज्यामितीय का परिचय BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - अभ्यास 7.1 (लघु उत्तरीय प्रश्न)
7 Videos
- बीजीय सर्वसमिकाएँBOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - वस्तुनिष्ठ प्रश्न
18 Videos
- रेखाएं और कोणBOOK - KC SINHACHAPTER - रेखाएं और कोणEXERCISE - वस्तुनिष्ठ प्रश्न
9 Videos
Similar Questions
एक ऐसे बिंदु का अस्तित्व है जिससे कोई रेखा नहीं गुजर सकती हैं ।
यह कथन सत्य हैं या असत्य । अपने उत्तरों के लिए कारण दें ।
View Solutionअधिगृहीत और अवधारणा से आप क्या समझते हैं ?
View Solution4x2+9+12xके गुणनखंड निम्नलिखित में कौन है ?
View Solutionबगल के चित्र में x बराबर है
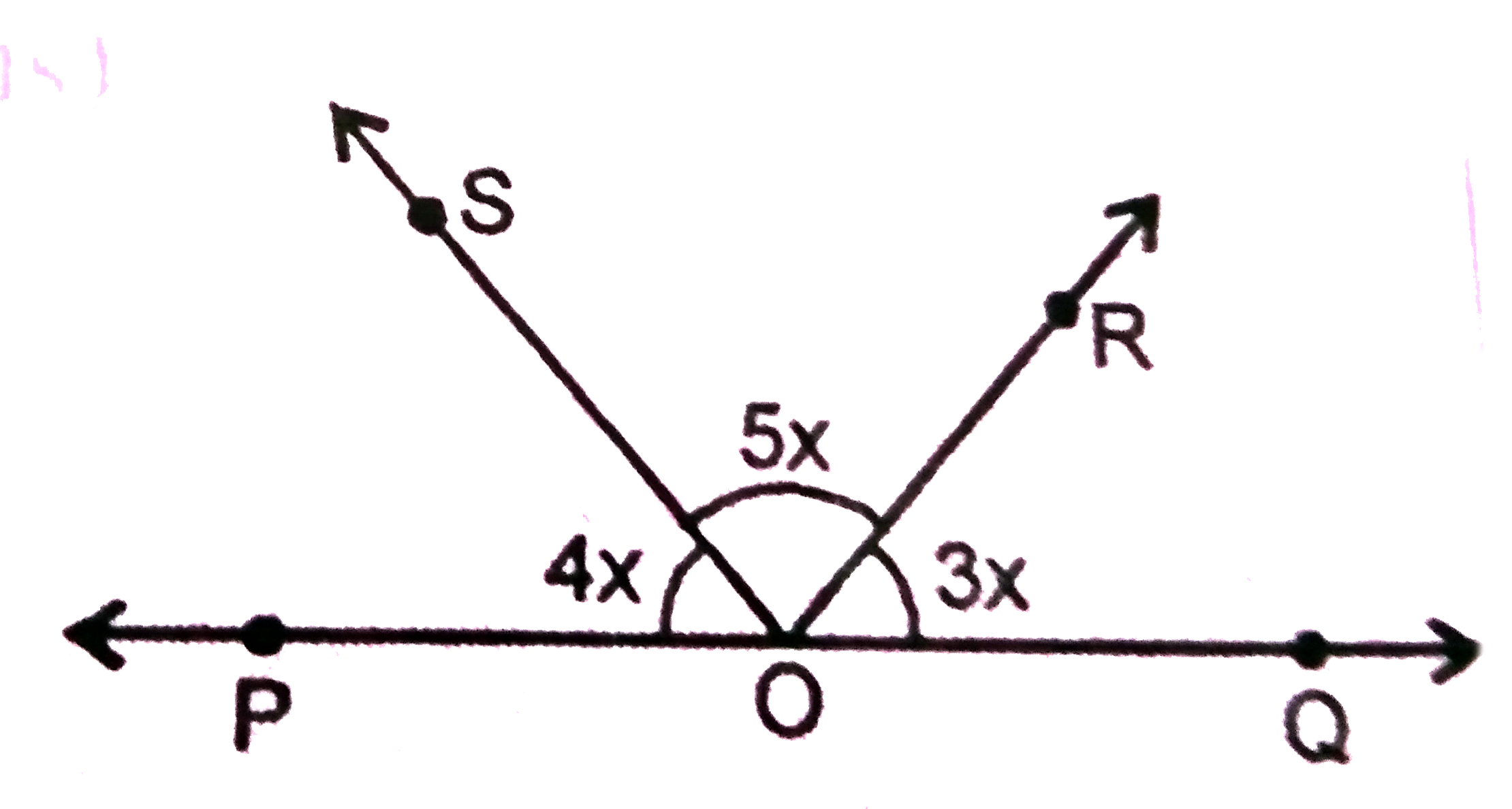
View Solutionयदि ¯a और ¯b दो सदिश इस प्रकार हैं कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b लंबवत होगा b पर ।
View Solutionबिंदु P(a,b) सरल रेखा 3x+2y=13 पर तथा बिंदु Q(b,a)सरल रेखा 4x−y=5 पर स्थित है तो रेखा PQ का समीकरण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionयदि बिंदुओं A और B के स्थिति सदिश क्रमशः ¯a और ¯b हों तो उस बिंदु C का स्थिति सदिश ज्ञात कीजिए जो BA को आगे बढ़ने पर इस प्रकार स्थित है कि BC=1.5BA.
View Solutionसदिशों के प्रयोग द्वार सिद्ध कीजिए कि बिंदु A(−2,3,5),B(7,0,−1),C(−3,−2,−5) और D(3,4,7) इस प्रकार हैं कि AB और CD बिंदु P(1,2,3) पर प्रतिच्छेद करते हैं।
View Solutionयदि ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b तथा C,AB पर एक ऐसा बिंदु है कि ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है:
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionदिखाइए कि निम्नलिखित बिंदुओं के समूह एक समद्विबाहु त्रिभुज के शीर्ष हैं :
(0,5), (6,3) और (5,10)
View Solution
