सिद्ध कीजिए कि एक दिए हुए रेखाखंड पर एक समबाहु त्रिभुज की रचना की जा सकती हैं ।
माना कि एक दी हुई लम्बाई का एक रेखाखंड AB हैं ।
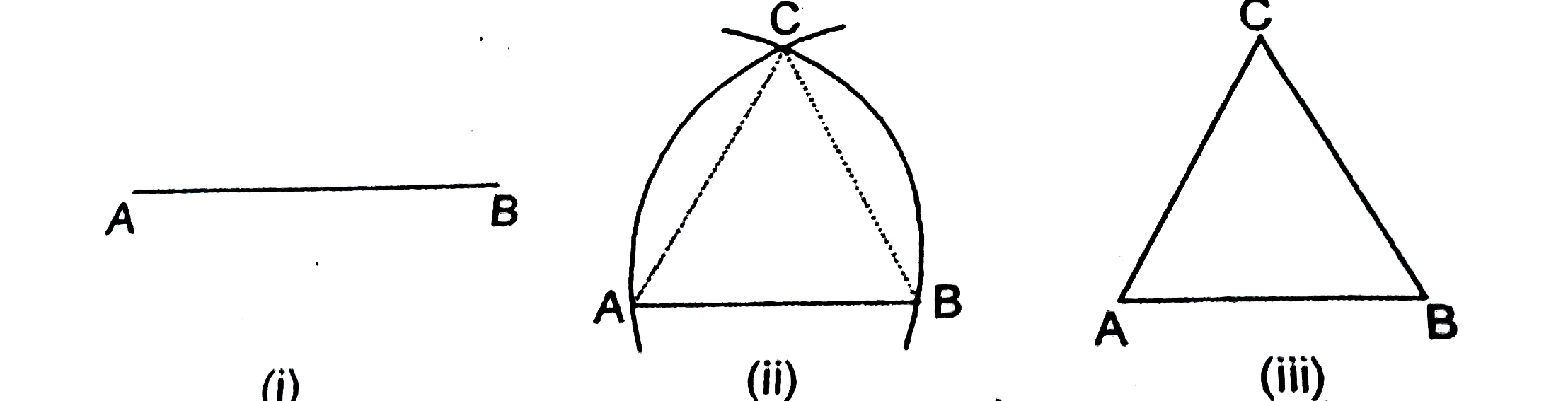
अतः यूक्लिड की अभिधारणा (3) से हम बिंदु A को केंद्र और AB त्रिज्या लेकर एक वृत्त खींच सकते हैं । इसी प्रकार , B को केंद्र मानकर और BA त्रिज्या लेकर एक अन्य वृत्त खींचा जा सकता हैं । माना कि ये दोनों वृत्त बिंदु C पर मिलते हैं । अब रेखाखंड AC और BC खींचकर △ABC बनाएँ ।
अब हमें यह सिद्ध करना हैं कि यह त्रिभुज एक समबाहु त्रिभुज हैं , अर्थात् AB = AC = BC
अब , AB = AC , क्योंकि ये एक वृत्त की त्रिज्याएँ हैं । ....(i)
इसी प्रकार , AB = BC , ...(ii)
(i) और (ii) से और यूक्लिड के पहले अभिगृहीत (वे वस्तुएँ जो एक ही वस्तु के बराबर होती हैं एक - दूसरे के बराबर होती हैं ) से
AB = BC = AC
अतः △ABC एक समबाहु त्रिभुज हैं ।
Note : यहाँ यूक्लिड ने , बिना कहीं बताए , यह मान लिया गया हैं कि केंद्रों A और B को लेकर खींचे गए वृत्त परस्पर एक बिंदु पर मिलेंगे ।
Topper's Solved these Questions
- यूक्लिड की ज्यामितीय का परिचय BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - अभ्यास 7.1 (अतिलघु उत्तरीय प्रश्न )
5 Videos
- यूक्लिड की ज्यामितीय का परिचय BOOK - KC SINHACHAPTER - यूक्लिड की ज्यामितीय का परिचय EXERCISE - अभ्यास 7.1 (लघु उत्तरीय प्रश्न)
7 Videos
- बीजीय सर्वसमिकाएँBOOK - KC SINHACHAPTER - बीजीय सर्वसमिकाएँEXERCISE - वस्तुनिष्ठ प्रश्न
18 Videos
- रेखाएं और कोणBOOK - KC SINHACHAPTER - रेखाएं और कोणEXERCISE - वस्तुनिष्ठ प्रश्न
9 Videos
Similar Questions
एक ऐसे बिंदु का अस्तित्व है जिससे कोई रेखा नहीं गुजर सकती हैं ।
यह कथन सत्य हैं या असत्य । अपने उत्तरों के लिए कारण दें ।
View Solutionअधिगृहीत और अवधारणा से आप क्या समझते हैं ?
View Solution4x2+9+12xके गुणनखंड निम्नलिखित में कौन है ?
View Solutionबगल के चित्र में x बराबर है
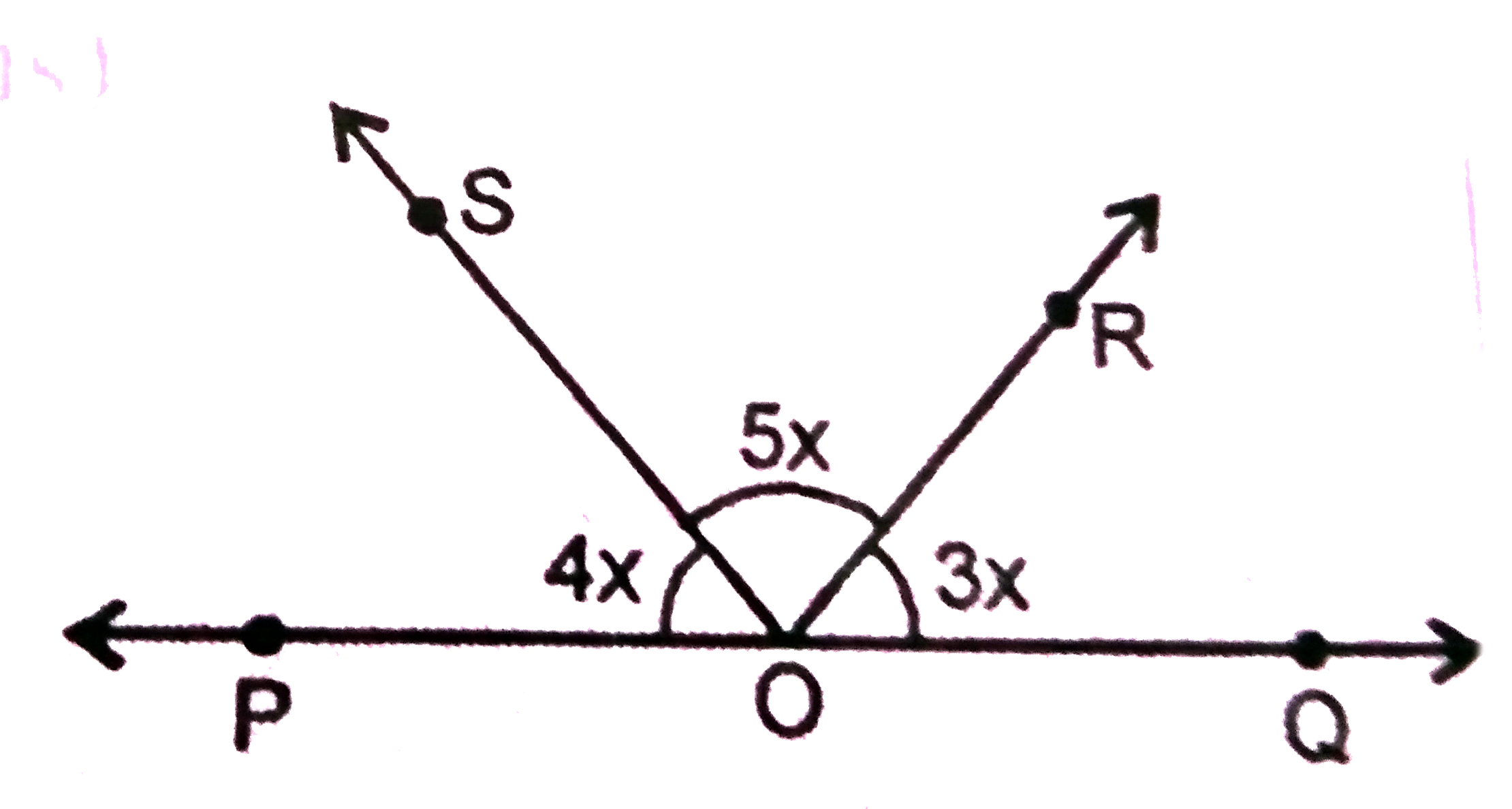
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solutionएक2.7 सेमी त्रिज्या लेकर वृत्त की रचना कीजिए। उस वृत्त पर एक स्पर्श रेखा खींचिए।
View Solutionएक त्रिभुज की दो भुजाओं की मापों का योग
View Solutionअथवा 'कारतूस' पाठ के आधार पर सोदाहरण सिद्ध कीजिए कि वज़ीर अली एक जांबाज़ सिपाही था।
View Solutionबढ़ती आबादी के पर्यावरण पर पड़ने वाले दुष्प्रभावों की चर्चा करते हुए स्पष्ट कीजिए कि,"नेचर की सहनशक्ति की भी एक सीमा होती है।"
View Solutionत्रिभुज की रचना |SSS कसौटी
View Solutionत्रिभुज की रचना |SAS कसौटी
View Solutionत्रिभुज की रचना |ASA कसौटी
View Solutionत्रिभुज की रचना |RHS कसौटी
View Solutionएक त्रिभुज की रचना
View Solutionएक त्रिभुज की रचना|Part 2
View Solutionएक त्रिभुज की रचना|जब दो कोण एवं तीनों भुजाओं का योग दिया हो
View Solution
