रैखिक प्रोग्रामिंग इष्टतम मान (अधिकतम या न्यूनतम) को खोजने की एक विधि है जब संबंध रैखिक समीकरणों या असमानताओं के रूप में व्यक्त किया जाता है।
उपरोक्त जानकारी के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए।
निम्नलिखित रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल करें।
निम्नलिखित व्यवरोध है
तथा
अक्ष पर स्थित बिंदुओ के निर्देशांक ज्ञात कीजिए
अक्ष पर स्थित बिंदुओ के निर्देशांक ज्ञात कीजिए
प्रतिच्छेद बिन्दु के निर्देशांक ज्ञात कीजिए
का अधिकतम मान क्या होगा
का न्यूनतम मान क्या होगा
हम सर्वप्रथम निम्नलिखित रेखओं का आलेख खींचते हैं।
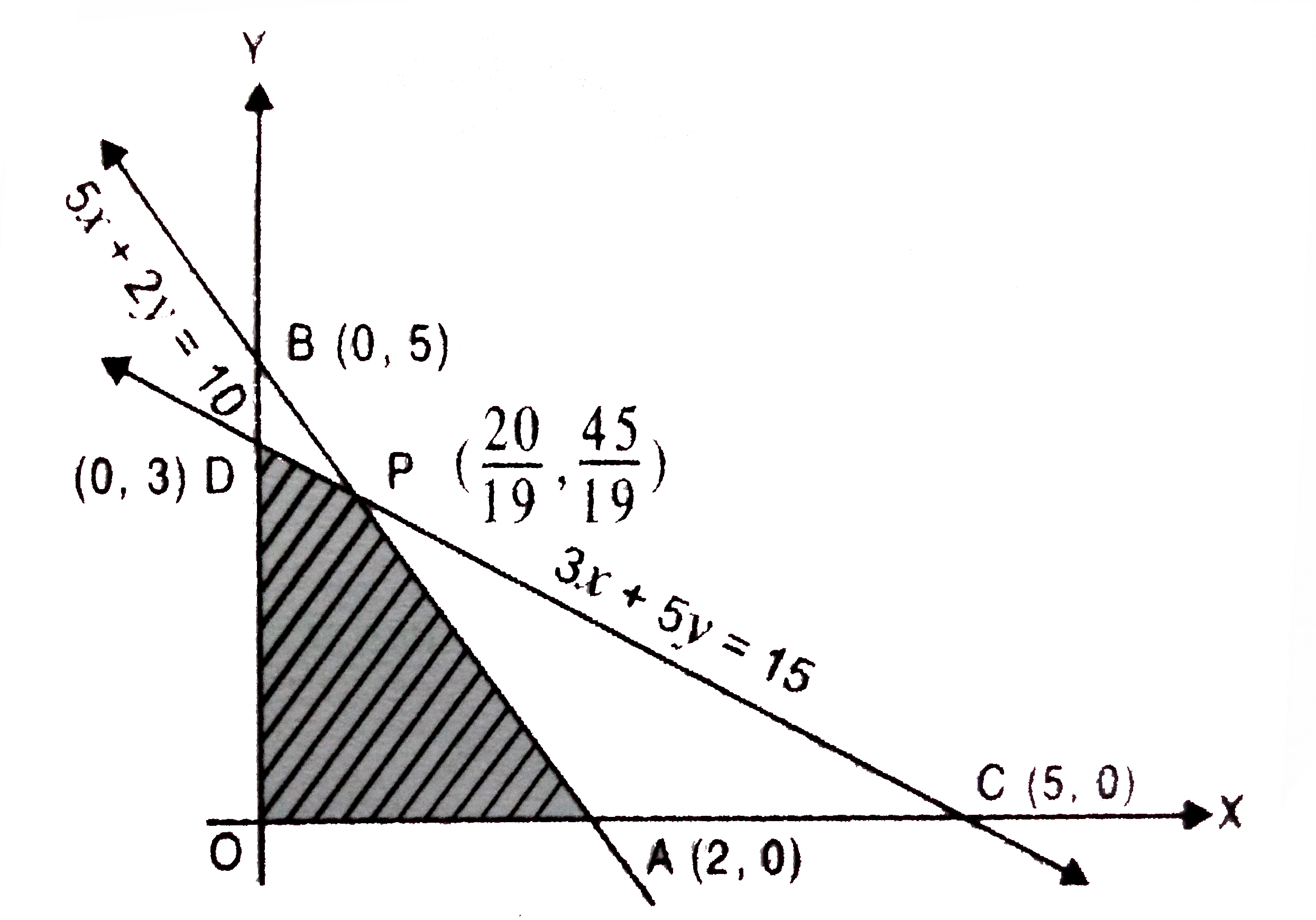
छायांकित क्षेत्र सुसंगत क्षेत्र है। स्पष्टतः यह परिमित क्षेत्र है।
इसके शीर्ष तथा है।
दिया है:
पर,
पर,
पर ,
पर ,
स्पष्टतः Z का मान पर महत्तम है।
अतः दिए गए रैखिक प्रोग्रामन समस्या का optimal हल है।
का अधिकतम मान
Topper's Solved these Questions
- रैखिक प्रोग्रामनBook:KC SINHAChapter:रैखिक प्रोग्रामनExercise:दो चरों में एक रैखिक असमिका के हल पर आधारित प्रश्नः
Explore 4 Videos
- रैखिक प्रोग्रामनBook:KC SINHAChapter:रैखिक प्रोग्रामनExercise:दो चरों में रैखिक असमिकाओं के निकाय के हल पर आधारित प्रश्नः
Explore 4 Videos
- यादृच्छिक चर और प्रायिकता बंटन Book:KC SINHAChapter:यादृच्छिक चर और प्रायिकता बंटन Exercise:Objective Questions
Explore 4 Videos
- रैखिक समीकरणों के निकाय का हल Book:KC SINHAChapter:रैखिक समीकरणों के निकाय का हल Exercise:Objective Questions
Explore 4 Videos
Similar Questions
निम्नलिखित रैखिक असमिकाओं को आलेखीय विधि से हल करें:
3x−4y<12
View Solutionनिम्नलिखित रैखिक असमिकाओं के निकाय को आलेखीय विधि से हल करें।
3x+4y≤60,x+3y≤30,x≥0,y≥0
View Solutionएक यादृच्छिक चर X का बंटन नियम निम्नलिखित है :
x234P(X=x)0.30.40.3
इस बंटन का मानक विचलन ज्ञात करें।
View SolutionFor the system of equations :
a1x+b1y+c1z=0,a2x+b2y+c2z=0,a3x+b3y+c3z=0
if ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=0, then this system has:
View SolutionThe value of |[a,a+d,a+2d] , [a+d,a+2d,a+3d] , [a+2d,a+3d,a+4d]|+|[b
View Solutionनिम्नलिखित प्रश्नो के उत्तर दीजिए :
अहिंसा एक विज्ञान है इस विचार का पाठ के आधार पर विवेचना कीजिए ।
View Solutionरैखिक असमिकाओं के निम्नलिखित निकाय को आलेखीय विधि से हल कीजिए:
x−y≤2,x+y≤4,x≥0,y≥0
View SolutionThe correct order of size among Br^(+), Br, Br^(-)
View Solutionअन्तराल ज्ञात कीजिये जिनमे से निम्लिखित फलन वर्धमान है या हसयमन है। >br>f(x)=x4−2x2
View Solutionनिम्न रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल कीजिए।
निम्नतम Z=200x+500y
व्यवरोध x+2y≥10
3x+4y≤24
तथा x≥0,y≥0
View Solutionनिम्न रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल कीजिए।
अधिकतम Z=y+34x
व्यवरोध x−y≥0
−x2+y≤1
तथा x≥0,y≥0
View Solutionनिम्न रैखिक प्रोग्रामन समस्या को आलेखीय विधि से हल कीजिए।
अधिकतम Z=2x+3y
व्यवरोध 4x+6y≤60
2x+y≤20
तथा x≥0,y≥0
View Solutionनिम्न प्रमेय को समझाइए।
प्रमेय 1. यदि एक रैखिक प्रोग्रामन समस्या के लिए R सुसंगत क्षेत्र है तथा उद्देश्य फलन Z=ax+by है। जब Z के एक इष्टतम मान ( अधिकतम या न्यूनतम ) हो जहाँ व्यवरोधों से सम्बंधिर चर और y रैखिक समीकरणों द्वारा व्यक्त हों तब इस इष्टतम मान सुसंगत क्षेत्र के कोनों (शीर्षों )पर होता है।
View Solutionआलेखीय विधि से निम्नलिखित रैखिक प्रोग्रामन समस्या को न्यूनतमीकरण के लिए हल कीजिए :
उद्देश्य फलन Z=5x+y
व्यवरोध 3x+5y≥15
5x+2y≤10
x≥0,y≥0
View Solutionవేర్ల ద్వారా శాఖీయోత్పత్తి జరిపే మొక్కbr i) డాలియాbr ii) ముల్లంగిbr iii) క్యారెట్br iv) క్యాబేజిbr
View Solutionनिम्नलिखित प्रश्नों के उत्तर दीजिए-
प्रकृति का वेश किस प्रकार बदल रहा है? पंत की कविता के आधार पर लिखिए।
View Solution
