एक निर्माता दो सामान A और B बनाता है। सामान A, 200 रू0 प्रति इकाई की दर से बिकती है और निर्माण में 30 मिनट लगते हैं। सामान B, 300 रू0 प्रति इकाई की दर से बिकती है और निर्माण में 1 घंटा लगते हैं। A की 14 इकाई और B की 16 इकाई के लिए मांग है। एक सप्ताह में 40 घंटे निर्माण कार्य होता है एवं साप्ताहिक टर्न-ओवर 10000 रू0 से कम नहीं होना है। यदि A के प्रत्येक नग पर लाभ 20 रू0 एवं B के प्रत्येक नग पर लाभ 30 रू0 हो तो प्रत्येक के कितने नगों का निर्माण किया जाए कि लाभ अधिकतम हो? अधिकतम लाभ निकालें। समस्या का हल आलेखीय विधि से निकालें।
माना कि,
उत्पाद A तथा B के क्रमशः x और y इकाई उत्पादित किए जाते हैं
तथा कुल लाभ Z है,
तो x और y निम्नलिखित शर्तों को संतुष्ट करेंगें।
200x+300y≥10,000
या 2x+3y≥100
12x+1.y≤40 (चूँकि 30 मिनट = 12 घंटा)
या x+2y≤80
x≥14
y≥16
x,y≥0,
रैखिक प्रोग्रामन समस्या का गणितीय रूप निम्नलिखित होगा:
अधिकतमीकरण करें
z=20x+30y (लाभ)
जबकि
2x+3y≥100
x+2y≤80
x≥14
y≥16
x≥0,y≥0
अब हम निम्नलिखित रेखाओं का आलेख खींचते हैं
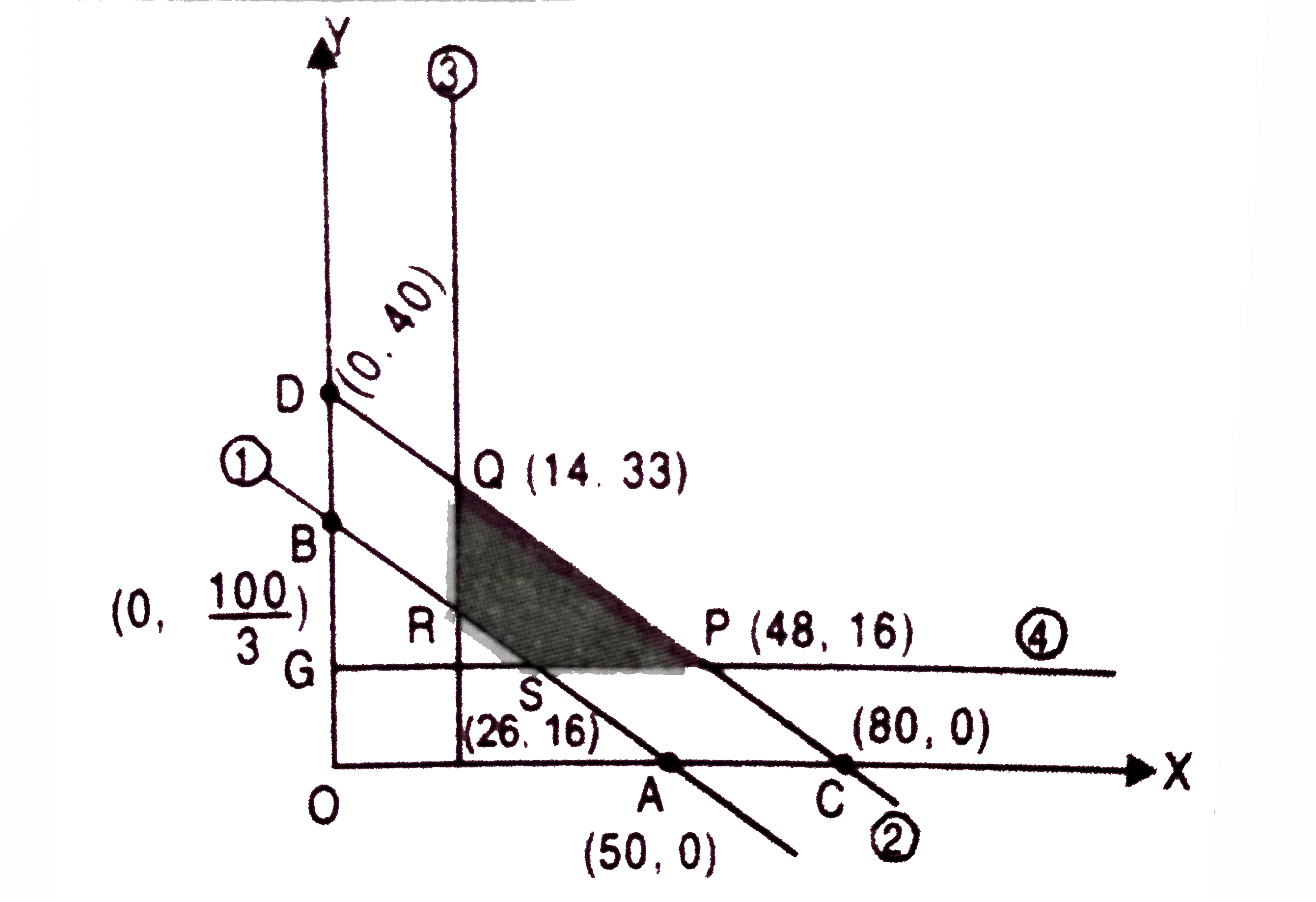
2x+3y=100…..(1)
x+2y=80…(2)
x=14…….(3)
y=16…. (4)
सुसंगत क्षेत्र SPQR है जो परिबद्ध है।
सुसंगत क्षेत्र का शीर्ष
S(26,16), P(48,16) Q(14,33) तथा R(14,24) है।
दिया है,
z=20x+30y
अतः S(26,16) पर z=1000
P(48,16) पर,z=1440
Q(14,33) पर,z=1270
R(14,24) पर,z=1000
अतः महत्तम लाभ 1440 रू0 है
तथा इसके लिए उत्पाद A का 48 इकाई और उत्पाद B का 16 इकाई उत्पादित करना होगा।
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - KC SINHACHAPTER - रैखिक प्रोग्रामनEXERCISE - दो चरों में एक रैखिक असमिका के हल पर आधारित प्रश्नः
4 Videos
- रैखिक प्रोग्रामनBOOK - KC SINHACHAPTER - रैखिक प्रोग्रामनEXERCISE - दो चरों में रैखिक असमिकाओं के निकाय के हल पर आधारित प्रश्नः
4 Videos
- यादृच्छिक चर और प्रायिकता बंटन BOOK - KC SINHACHAPTER - यादृच्छिक चर और प्रायिकता बंटन EXERCISE - Objective Questions
4 Videos
- रैखिक समीकरणों के निकाय का हल BOOK - KC SINHACHAPTER - रैखिक समीकरणों के निकाय का हल EXERCISE - Objective Questions
4 Videos
Similar Questions
निम्नलिखित रैखिक असमिकाओं को आलेखीय विधि से हल करें:
3x−4y<12
View Solutionनिम्नलिखित रैखिक असमिकाओं के निकाय को आलेखीय विधि से हल करें।
3x+4y≤60,x+3y≤30,x≥0,y≥0
View Solutionएक यादृच्छिक चर X का बंटन नियम निम्नलिखित है :
x234P(X=x)0.30.40.3
इस बंटन का मानक विचलन ज्ञात करें।
View SolutionFor the system of equations :
a1x+b1y+c1z=0,a2x+b2y+c2z=0,a3x+b3y+c3z=0
if ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=0, then this system has:
View Solutionएक निर्माता तीन प्रकार की वस्तुए x,y तथा z का उत्पादन करता है जिनका वह दो बाजारों में विक्रय करता है। वस्तुओं की वार्षिक बिक्री नीचे सूचित है
बाजार, उत्पादन
I, 10,000,2,000,18,000,II, 6,00, 20,000, 8,000<br>a.यदिx,yतथाz की प्रत्येक इकाई का विक्रय मूल्य रू0 2.50, रूच 1.50 और रू0 1.00 है तो प्रत्येक बाजार में कुल आय, आव्यूह बीजगणित की सहायता से ज्ञात कीजिए।
b. यदि उपर्युक्त तीन वस्तुओं की प्रत्येक इकाई की लागत क्रमशः रू0 2.00, रू0 1.00 और पैसे 50 है तो कुल लाभ ज्ञात कीजिए।
View Solutionएक छोटी फर्म सोने के अंगूठियां और चेनों का निर्माण करती है| प्रतिदिन अंगूठियों और चेनों के निर्माण की कुल संख्या अधिकतम 24 है| एक अंगूठी बनाने में एक घंटा तथा के चेन के बनाने में 30 मिनट लगते है| प्रतिदिन उपलब्ध घंटों की अधिकतम संख्या 16 है|यदि अंगूठी पर लाभ रु 300 तथा एक चेन पर लाभ रु 190 हो, तो ज्ञात कीजिए| की प्रतिदिन कितनी अंगूठियों और चेनों का निर्माण किया जाय ताकि अधिकतम लाभ कमाया जा सकें|
View Solutionयह ज्ञात है की महाविद्यालय के छात्रों में से 60 % छात्रावास में रहते है और 40 % छात्रावास में नहीं रहते है । पूर्ववर्ती वर्ष से परिणाम सूचित करते है की छात्रावास में रहने वाले छात्रों में से30 % छात्रों में से 20 % छात्रों ने A ग्रेड लिए। वर्ष के अंत में महाविद्यालय के एक छात्र को यादृच्छया चुना गया और पाया गया की उसे A ग्रेड मिला है । इस बात की क्या प्रायिकता है की वह छात्रावास में रहने वाला है ?
View Solutionसजीव की संरचनात्मक इकाई है
View Solutionसजीवों की संरचनात्मक इकाई ऊतक है। ( )
View Solutionसमाज में वर्ग हैं, श्रेणियाँ हैं। श्रेणियों में परिवार है। समाज की एक बुनियादी इकाई परिवार भी है। समाज की अच्छाई-बुराई । परिवार के माध्यम से व्यक्त होती है। मनुष्य के चरित्र का विकास. 1 परिवार में होता है। बच्चे पलते हैं, उन्हें सांस्कृतिक शिक्षा मिलती है। वे अपनी सारी अच्छाइयाँ-बुराइयाँ वहाँ से लेते हैं। हमारे । साहित्य तथा राजनीति के पास ऐसी कोई दृष्टि नहीं है जो परिवार को लागू हो....
समाज की एक बुनियादी इकाई है
View Solutionभाषा की सबसे छोटी इकाई है
View Solutionप्रथम कोटि अभिक्रिया के लिए निम्नलिखित में से कौन सा सही है/हैं? (a अभिकारक की प्रारंभिक सांद्रता है, x अभिकृत अभिकारक की सांद्रता है और t समय है)
View SolutionNO_2 और N_2O_4 नाइट्रोजन डाइऑक्साइड के दो रूप हैं। एक गैसीय अवस्था में मौजूद होता है जबकि दूसरा द्रव अवस्था में। NO_2 और N_2O_4 रूपों की प्रकृति है:
View Solutionएक अकार्बनिक यौगिक (A) जो पृथ्वी की सतह में दो सबसे अधिक पाए जाने वाले तत्वों से बना है और इसका उपयोग इमारत निर्माण में किया जाता है जब यह कार्बन के साथ अभिक्रिया करता है तो एक विषाक्त गैस (B) निर्मित होती है, जो एक द्विपरमाण्विक अणु है। यौगिक (A) और (B) हैं:
View Solutionएक अभिक्रिया A में प्रथम कोटि तथा B में द्वितीय कोटि है: जब A और B दोनों की सांद्रता दोगुनी हो जाती है, तो दर कैसे प्रभावित होती है?
View Solutionडाइमेथिल ईथर के अपघटन के फलस्वरूप CH_4, H_2 " और " CO का निर्माण होता है और अभिक्रिया दर = k[CH_3OCH_3]^(3/2) द्वारा दर्शायी जाती है। अभिक्रिया की दर, बंद पात्र में दाब में वृद्धि का अनुगमन करती है, इसलिए डाइमेथिल ईथर के आंशिक दाब के संदर्भ में भी दर को व्यक्त किया जा सकता है, अर्थात दर = k(PCH_3 OCH_3 )^(3/2) यदि दाब को बार तथा समय को मिनटों में मापा जाए, तब दर स्थिरांक की इकाई क्या होगी?
View Solution
