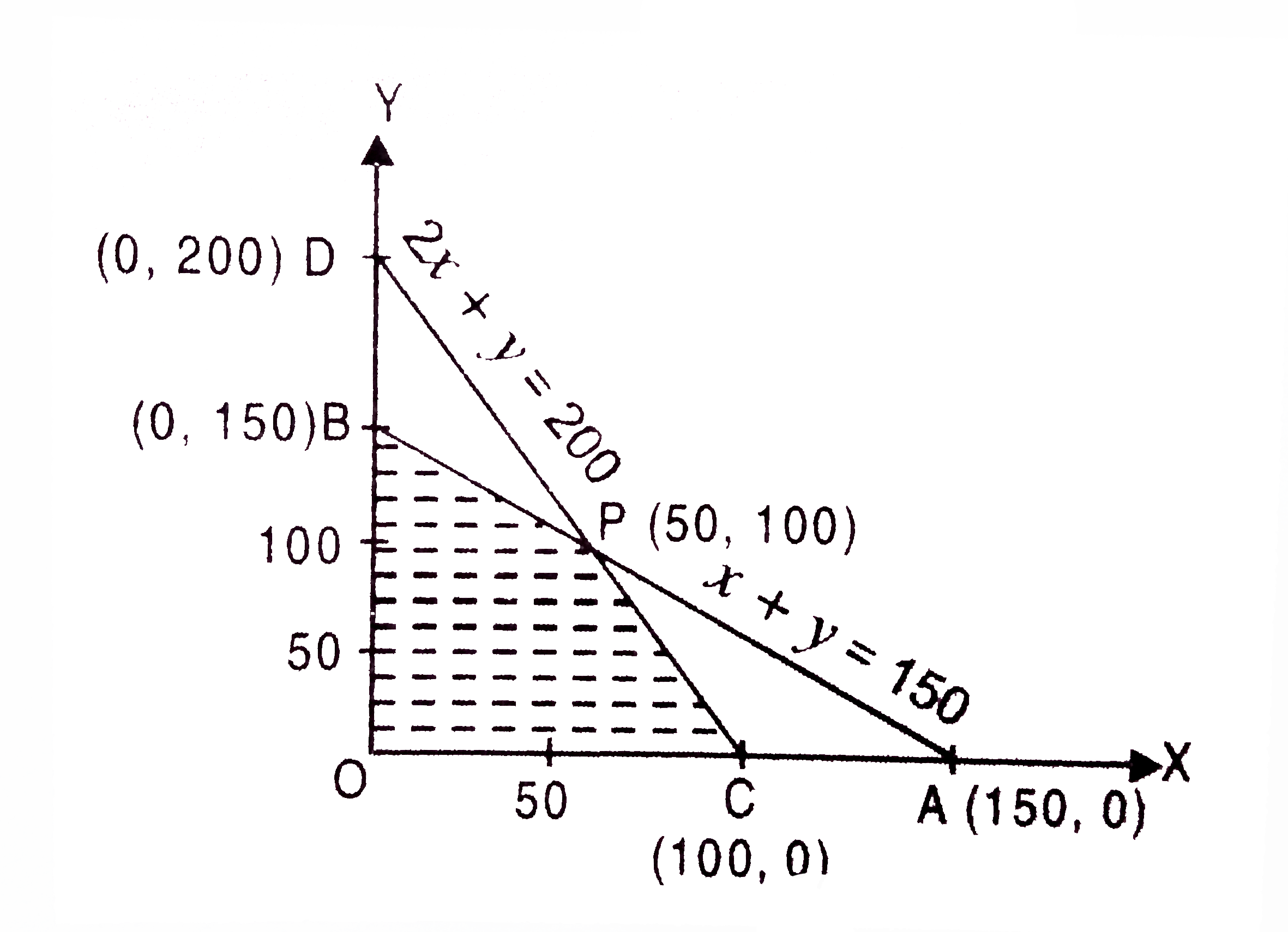
एक दूकानदान दो सामानों थर्मस फ्लास्क और वायुशून्य बर्तनों को बेचता है। उसे एक फ्लास्क की कीमत 120 रू0 एवं एक वायुशून्य बर्तन की कीमत 60 रू0 पड़ती है। उसके पास अधिक से अधिक 12000 रू0 निवेश के लिए है एवं 150 सामानों को रखने की जगह है। एक फ्लास्क को बेचने से 20 रू0 एवं वायुशून्य बर्तन को बेचने से 15 रू0 का लाभ होता है। यह मानते हुए कि वह जितने सामान खरीदता है बेचा सकता है उसे प्रत्येक के कितने नग खरीदने चाहिए ताकि उसका लाभ अधिकतम हो सके? आलेखीय विधि से हल करें।
माना कि खरीदे गए थर्मस फ्लास्क की संख्या x है तथा वायु शून्य बर्तनों की संख्या y है। माना कि कुल लाभ z है।
प्रश्न से x और y निम्निलिखित शर्तों को संतुष्ट करेंगें।
x+y≤150
120x+60y≤12000
या 2x+y≤200
x≥0,y≥0
रैखिक प्रोग्रामन समस्या का गणितीय रूप निम्नलिखित होगा:
अधकतमीकरण करें
z=20x+15y
जबकि
x+y≤150
2xy≤200
x≥0,y≥0
अब हम निम्नलिखित रेखाओं का आलेख खींचते हैं।
x+y=150 ……….1
तथा 2x+y=200…….2
ये रेखाएं बिंदु P(50,100) पर मिलती हैं। छायांकि क्षेत्र OCPB सुसंगत क्षेत्र है जो परिबद्ध है।
सुसंगत क्षेत्र के शीर्ष O(0,0),C(100,0),P(50,100) तथा B(0,150) है।
दिया है z=20x+15y<br>अतःO(0,0)पर,z=0<br>C(100,6)पर,z=2000<br>P(50,100)पर,z=2500<br>तथाB(0,150)पर,z=2250<br>स्पष्टतःzकामानबिंदुP(50,100)परमहत्तमहै।<br>अतःमहत्तमलाभकेलिए50थर्मसफ्लास्क्तथा100वायुशून्यबर्तनखरीदनाहोगा।<br>महत्तमलाभ=2500 रू0
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - KC SINHACHAPTER - रैखिक प्रोग्रामनEXERCISE - दो चरों में एक रैखिक असमिका के हल पर आधारित प्रश्नः
4 Videos
- रैखिक प्रोग्रामनBOOK - KC SINHACHAPTER - रैखिक प्रोग्रामनEXERCISE - दो चरों में रैखिक असमिकाओं के निकाय के हल पर आधारित प्रश्नः
4 Videos
- यादृच्छिक चर और प्रायिकता बंटन BOOK - KC SINHACHAPTER - यादृच्छिक चर और प्रायिकता बंटन EXERCISE - Objective Questions
4 Videos
- रैखिक समीकरणों के निकाय का हल BOOK - KC SINHACHAPTER - रैखिक समीकरणों के निकाय का हल EXERCISE - Objective Questions
4 Videos
Similar Questions
निम्नलिखित रैखिक असमिकाओं को आलेखीय विधि से हल करें:
3x−4y<12
View Solutionनिम्नलिखित रैखिक असमिकाओं के निकाय को आलेखीय विधि से हल करें।
3x+4y≤60,x+3y≤30,x≥0,y≥0
View Solutionएक यादृच्छिक चर X का बंटन नियम निम्नलिखित है :
x234P(X=x)0.30.40.3
इस बंटन का मानक विचलन ज्ञात करें।
View SolutionFor the system of equations :
a1x+b1y+c1z=0,a2x+b2y+c2z=0,a3x+b3y+c3z=0
if ∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣=0, then this system has:
View Solutionनिम्नलिखित गदयांशों को पढ़कर उसके नीचे दिए गए प्रश्नों के उत्तर केवल एक-एक वाक्य मैं लिखिए : "इस मिस्त्री को यहाँ से मत हटाना । इसे काम की अच्छी जानकारी है और यह परिश्रमी भी है ।" उपर्युक्त वाक्य किसने कहा है ?
View Solutionनिम्नलिखित गदयांशों को पढ़कर उसके नीचे दिए गए प्रश्नों के उत्तर केवल एक-एक वाक्य मैं लिखिए : "इस मिस्त्री को यहाँ से मत हटाना । इसे काम की अच्छी जानकारी है और यह परिश्रमी भी है ।" परिश्रमी कौन हैं ?
View Solutionदरअसल शुरू से ही था हमारे आदेशों में कही एक जानी दुश्मन कि घर को बचाना है लूटेरों से शहर को बचाना है नदियों से देश को बचाना है , देश के दुश्मनों से बचाना है - नदियों को नाला हो जाने से हवा को धुआँ हो जाने से खाने को जहर हो जाने से : बचाना है - जंगल को मरुस्थल हो जाने से , बचाना है - मनुष्य को , जंगल हो जाने से । शब्द - सारिणी की सहायता से समान अर्थ के शब्द ढूढ़कर लीखिए :
View Solutionनिम्नलिखित गद्द्यांशों को पढ़कर उसके नीचे दिए गए प्रश्नों के उत्तर केवल एक-एक वाक्य में लिखिए :
'' इस मिस्त्री को यहाँ से मत हटाना । इसे काम की अच्छी जानकारी है और यह परिश्रमी भी है । ''
Q. परिश्रमी कौन है ?
View Solutionएक निर्माता तीन प्रकार की वस्तुए x,y तथा z का उत्पादन करता है जिनका वह दो बाजारों में विक्रय करता है। वस्तुओं की वार्षिक बिक्री नीचे सूचित है
बाजार, उत्पादन
I, 10,000,2,000,18,000,II, 6,00, 20,000, 8,000<br>a.यदिx,yतथाz की प्रत्येक इकाई का विक्रय मूल्य रू0 2.50, रूच 1.50 और रू0 1.00 है तो प्रत्येक बाजार में कुल आय, आव्यूह बीजगणित की सहायता से ज्ञात कीजिए।
b. यदि उपर्युक्त तीन वस्तुओं की प्रत्येक इकाई की लागत क्रमशः रू0 2.00, रू0 1.00 और पैसे 50 है तो कुल लाभ ज्ञात कीजिए।
View Solutionएक अनभिनत पासे को 5 बार उछाला जाता है एक समसंख्या प्राप्त करना एक सफलता है तो प्रायिकता ज्ञात कीजिए - अधिक से अधिक 4 सफलताओ के लिए
View Solutionएक व्यक्ति के लक्ष्य भेदन की प्रायिकता 14 है। यह कम - से - कम कितनी बार गोली चलाए की लक्ष्य को कम से कम एक बार भेदने की प्रायिकता 23 से अधिक हो ?
View Solutionएक अनभिनत पास को 6 बार उछाला जाता है। यदि एक समसंख्या प्राप्त करना एक सफलता है , तो
अधिक - से - अधिक 5 सफलताओ की प्रायिकता ज्ञात कीजिए।
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionएक पास को 500 बार फेंकने पर परिणाम 2 आने की बारम्बारता 200 है। 2 की प्रायिकता क्या है ?
View SolutionRajendra marks up the price of an article by 50% and then allows a discount of 20% and sells it to Alok. Alok sells it for Rs 20 more than what he purchased for, this SP is 30% more than the original CP of the article. Then Alok's profit % is
View SolutionA conical flask is full of water. The flask has base radius r and height h. This water is poured into a cylindrical flask of base radius mr. The height of water in the cylindrical flask is. एक शांकव फ्लास्क पानी से भरी हुई है। फ्लास्क की आधार त्रिज्या r है और ऊँचाई h है। यह पानी का बेलनाकार फ्लास्क में डाला गया जिसकी आधार त्रिज्या mr है। बेलनाकार फ्लास्क में पानी की ऊँचाई है-
View Solution
