AB || DC है और रेखाखण्ड BD का मध्य-बिन्दु P है | तो दर्शाइए
(i)ΔAPB≅ΔCPD (ii)P रेखाखण्ड AC का मध्य बिन्दु है |
चूँकि AB ||DC है तथा तिर्यक रेखा AC इन्हे क्रमशः A तथा C पर काटती है |
∴ ∠PAB=∠PCD ..(i)[एकान्तर कोण]
इसी प्रकार, AB||DC है तथा तिर्यक रेखा BD इन्हें क्रमशः B तथा D पर काटती है |
∴ ∠ABP=∠CDP ...(ii) [एकान्तर कोण]
चूँकि AC तथा BD एक दूसरे को P पर काटती है |
∴ ∠APB=∠CPD ..(iii) [शीर्षभिमुख कोण]
अब त्रिभुजों APB तथा CPD में
∠ABP=∠CDP [(i)से]
BP=DP [∵ P, BD का मध्य-बिन्दु दिया है]
तथा, ∠APB=∠CPD [(iii)से]
अतः कोण-भुजा-कोण सर्वागसमता कसौटी से

ΔAPB≅ΔCPD
⇒ AP=PC [∵ सर्वांगसम त्रिभुजों के संगत भाग समान होते हैं]
अतः बिन्दु P रेखाखण्ड एक का मध्य-बिन्दु है |
Topper's Solved these Questions
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - प्रश्नावली 10.1
13 Videos
- सर्वांगसम त्रिभुजेंBOOK - RD SHARMACHAPTER - सर्वांगसम त्रिभुजेंEXERCISE - प्रश्नावली 10.2
3 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - RD SHARMACHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - बहु विकल्पीय प्रश्न
20 Videos
- सांखि्यिकीय आँकड़ों का सारणीयनBOOK - RD SHARMACHAPTER - सांखि्यिकीय आँकड़ों का सारणीयनEXERCISE - बहु विकल्पीय प्रश्न
10 Videos
Similar Questions
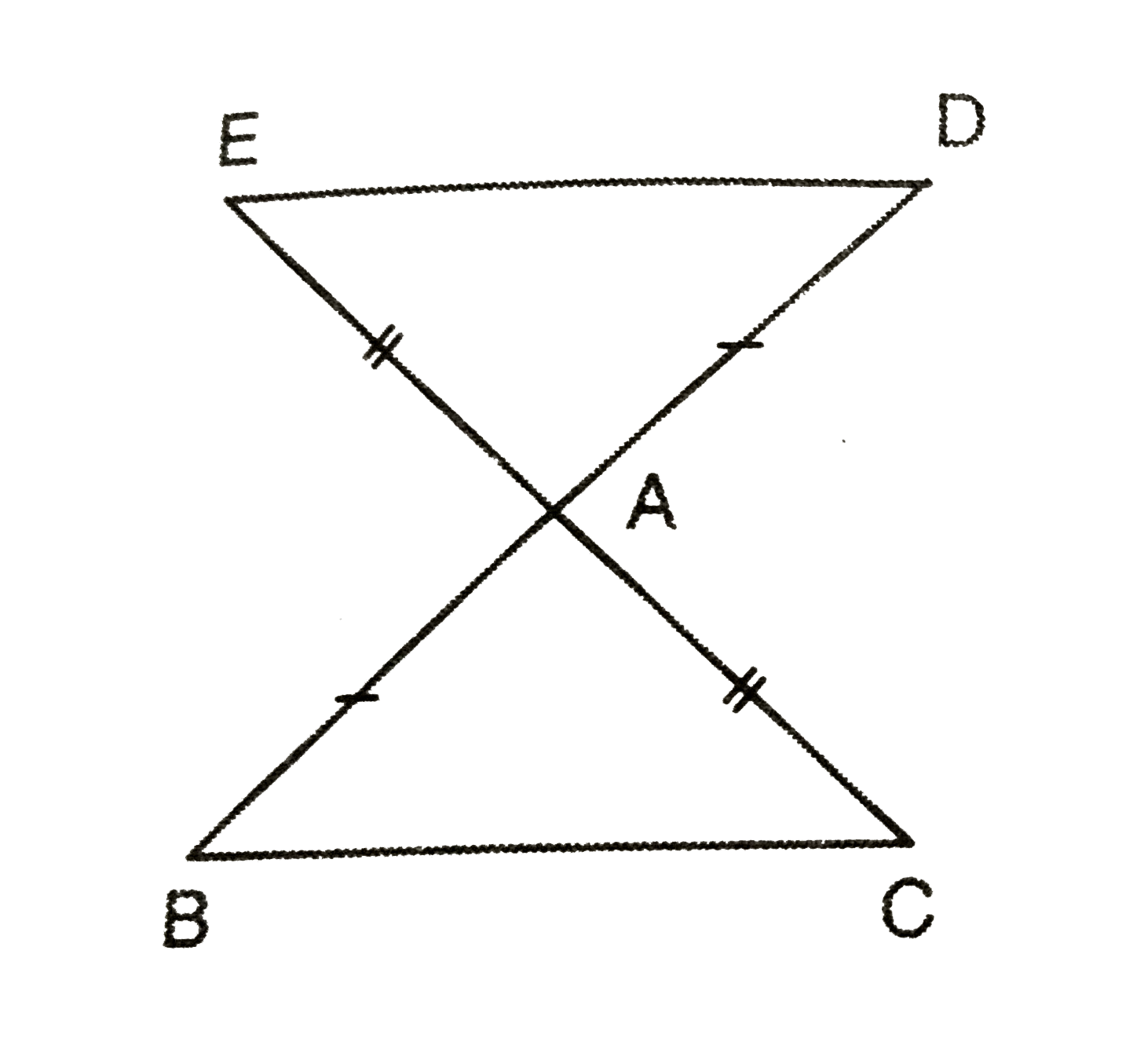
भुजाएँ BA तथा CA तथा इस प्रकार बढ़ाई गई कि BA=AD तथा CA=AE हैं | सिध्द कीजिए कि रेखाखण्ड DE∣∣BC है |
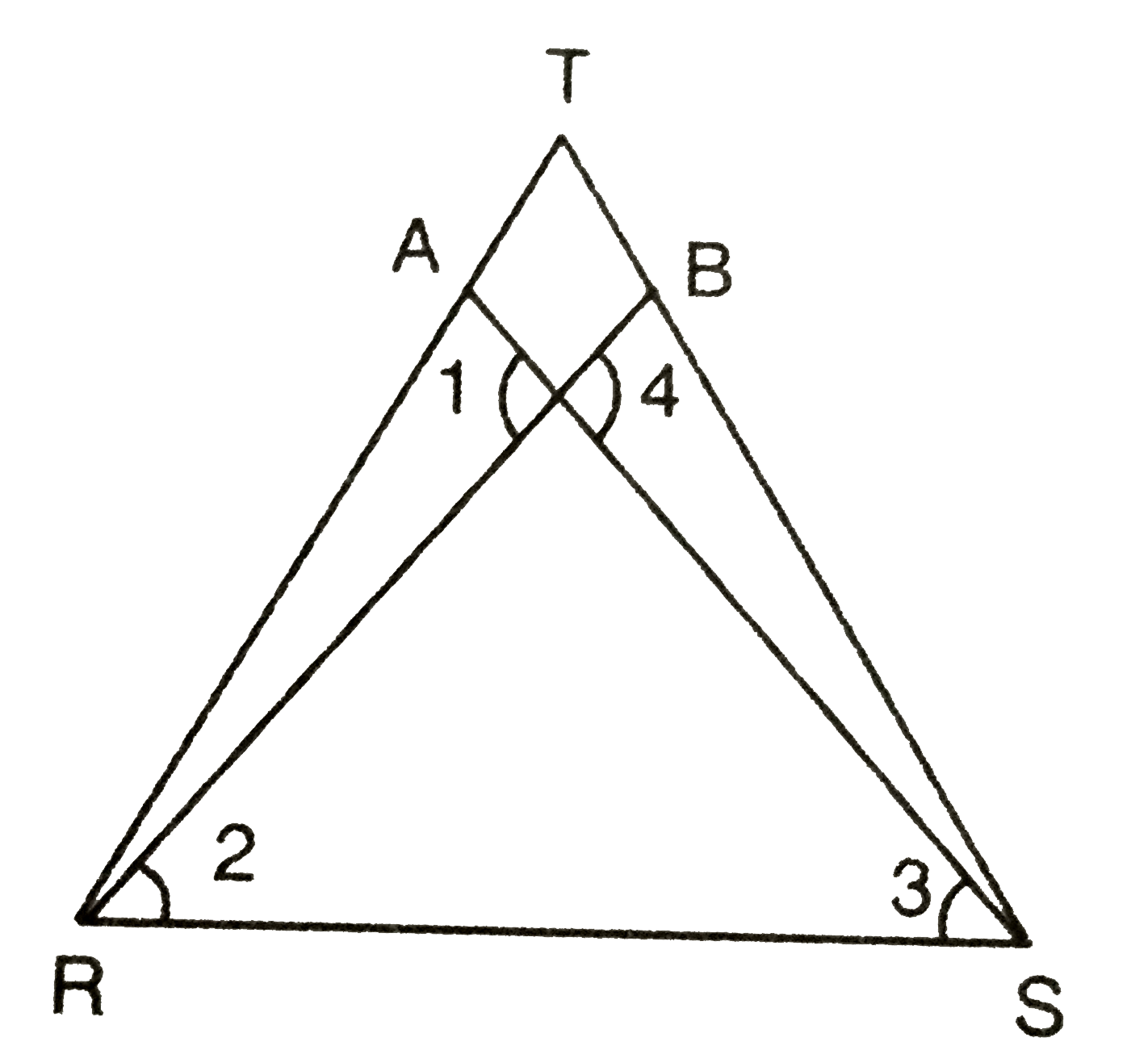
View Solutionयह दिया है RT=TS ∠1=2√3 तथा ∠4=2Sqrt(3)तो, दर्शाइए कि ΔRBT≅ΔSAT
View Solutionयदि दो समांतर चतुर्भुजों का एक ही आधार है और समान समांतर रेखाओं के बीच स्थित है तो उनके क्षेत्रफलों के बीच क्या अनुपात होगा :
View Solutionप्रेक्षणो के सग्रह में से उच्चतम एव न्यूनतम प्रेक्षणो के अन्तर को कहते है ?
View Solutionपरवलय y2=4ax की नाभि तथा उस पर स्थित चर को मिलाने वाले रेखाखण्ड के मध्य - बिंदु का पथ एक परवलय है जिसकी नियता है :
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
View Solutionएक अतिपरवलय बिन्दु P(√2,√3) से होकर जाता है, तथा उसकी नाभियाँ (±2,0) पर है, तो अतिपरवलय के बिन्दु P पर खींची गई स्पर्श रेखा जिस बिन्दु से होकर जाती है, वह है
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionमाना P(4,−4) तथा Q(9,6) परवलय पर स्थित दो बिन्दु है । O इस परवलय का शीर्ष बिन्दु है तथा X इस परवलय की चाप POQ का कोई ऐसा बिन्दु है, जिसके लिए का ΔPXQ क्षेत्रफल है, तो यह अधिकतम क्षेत्रफल (वर्ग इकाइयो में) है
View Solutionयदि बिन्दु P(−3,4) से होकर जाने वाली एक सरल रेखा इस प्रकार है कि इसके निर्देशांक अक्षो के बीच अंत: खंडित भाग का मध्य -बिन्दु P है, तो इसका समीकरण है
View Solutionयदि बिन्दु (4, 2) का रेखा L = 0 के सापेक्ष प्रतिबिम्ब (-2, 6) है, तो L का समीकरण है
View Solutionअतिपरवलय 25x2−16y2=400 की जीवा का समीकरण क्या होगा, जिसका मध्य बिन्दु (5,3) है ?
View Solutionबिन्दु (1,1) पर वक्रों y=x2 और x=y2 के मध्य कोण है
View Solutionवृत्त x2+y2=81 की उस जीवा का समीकरण क्या होगा, जिसका मध्य-बिन्दु (-2, 3) है?
View Solution
