एक यातायात संकेत पटल पर 'आगे स्कूल है' लिखा है और यह भुजा 'a' वाले एक समबाहु त्रिभुज के आकार की है | यदि इस संकेत पटल का परिमाप 180 सेमी. हो तो हीरोन के सूत्र के प्रयोग द्वारा इस त्रिभुज का क्षेत्रफल ज्ञात कीजिये |
मान लीजिये कि इस संकेत पटल का परिमाण '2s' है |
∴ 2s=a+a+a⇒s=3a2
मान लीजिए कि दी हुई समबाहु त्रिभुज का क्षेत्रफल Δ है |
∴ Δ=√s(s−a)(s−b)(s−c)
⇒Δ=√3a2(3a2−a)(3a2−a)(3a2−a) [∵a=b=c]
⇒Δ=√3a2×a2×a2×a2=√3a416=√34a2
दिया है कि : परिमाण = 180 सेमी.
∴2s=180⇒3a=180⇒a=60
∴Δ=√34×(60)2=900√3cm2
Topper's Solved these Questions
Similar Questions
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिये जिसकी भुजाएँ 150 सेमी., 120 सेमी. तथा 200 सेमी. है।
View Solutionचतुर्भुज ABCD का क्षेत्रफल ज्ञात किजीये जिसमे AB =3 सेमी. BC = 4 सेमी. CD = 4 सेमी. DA = 5 सेमी.तथा AC = 5 सेमी. |
View Solutionचित्र में, त्रिभुज ABC में ∠A समकोण है तथा AL भुजा BC पर लम्ब है । सिद्ध कीजिए कि ∠BAL=∠ACB है ।
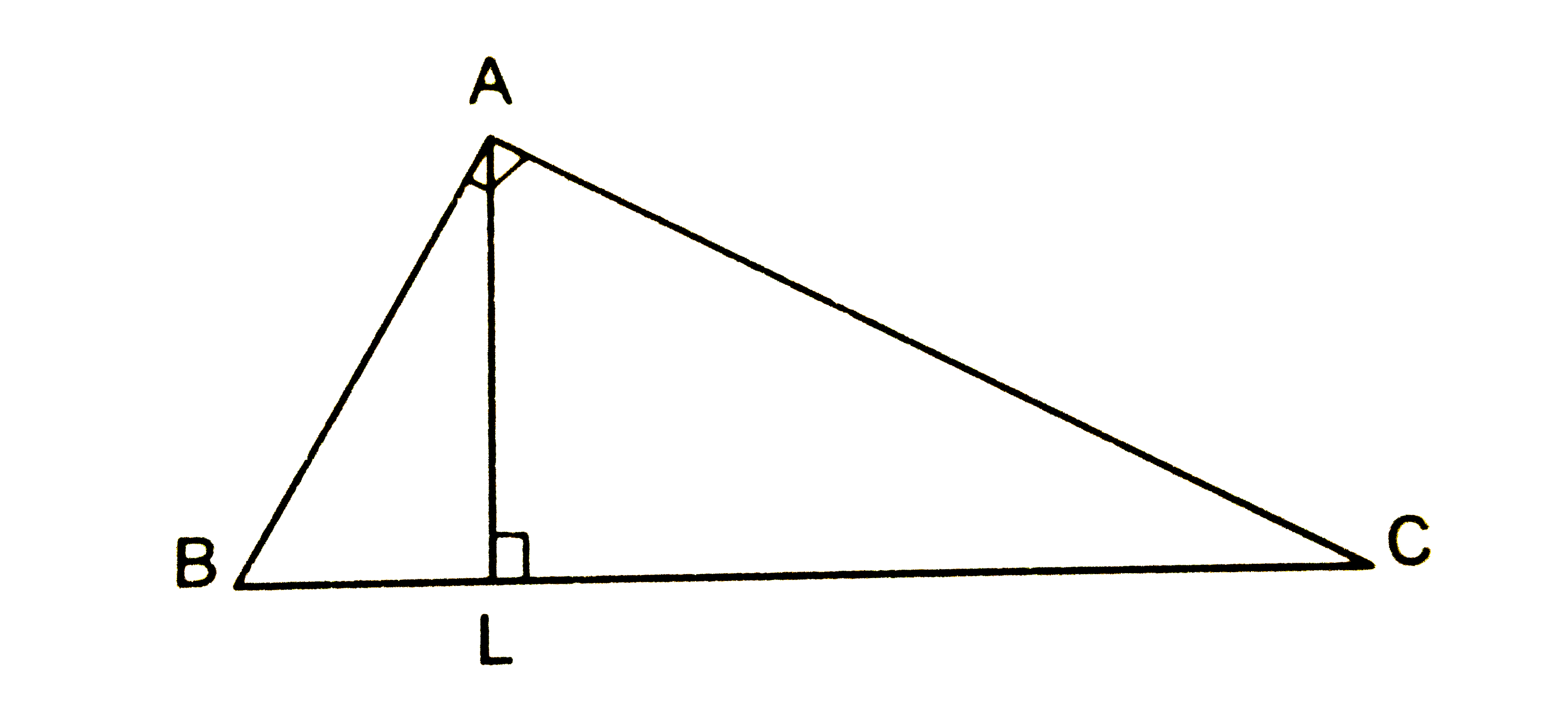
View Solutionसिद्ध कीजिये की बिंदु (a,a),(-a,-a),(-a√3,a√3) एक समबाहु त्रिभुज के निर्देशांक है
View SolutionA(1,1) और B(−2,3) दो स्थिर बिंदु है एक बिंदु P इस प्रकार गति करता है की त्रिभुज PAB का क्षेत्रफल 9 वर्ग इकाई है , तो P के बिन्दुपथ का समीकरण ज्ञात कीजिए।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
View Solutionहीरोन के सूत्र के प्रयोग से किसी त्रिभुज का क्षेत्रफल ज्ञात करना
View SolutionRevision|त्रिभुज का क्षेत्रफल#!#हीरोन के सूत्र द्वारा#!#महत्वपूर्ण प्रश्न
View SolutionRevision|हीरोन के सूत्र पर आधारित महत्वपूर्ण प्रश्न#!#त्रिभुज का क्षेत्रफल तथा चतुर्भुज का क्षेत्रफल
View Solutionहीरोन का सूत्र|हीरोन के सूत्र की सहायता से त्रिभुज का क्षेत्रफल ज्ञात करना सीखे#!#महत्वपूर्ण प्रश्न
View SolutionTwelve sticks, each of length one unit, are used to form an right-angled triangle. The area of the triangle is :
बारह छड़ियाँ, जिनमें से प्रत्येक की लंबाई एक इकाई है, का इस्तेमाल एक समकोण त्रिभुज बनाने के लिए किया जाता है | इस त्रिभुज का क्षेत्रफल ज्ञात करें |
View SolutionThe sides of a triangle are in the ratio 3 : 4 : 5. If the perimeter of the triangle is 24 cm, its area is:
एक त्रिभुज की भुजाएं 3 : 4 : 5 के अनुपात में हैं | यदि इस त्रिभुज का परिमाप 24 सेमी है, तो इसका क्षेत्रफल ज्ञात करें |
View SolutionThe diagonal of a square is equal to the side of an equilateral triangle. If the area of the square is 18 sqrt 3 sq.cm. What is the area (in cm^2 ) of the equilateral triangle? किसी वर्ग का विकर्ण एक समबाहु त्रिभुज की भुजा के बराबर है | यदि वर्ग का क्षेत्रफल 18 sqrt 3 वर्ग सेमी है, तो समबाहु त्रिभुज का क्षेत्रफल ( वर्ग सेमी में ) ज्ञात करें |
View SolutionIf the area of an equilateral triangle is 36 sqrt3 cm^2 , then the perimeter of the triangle is: यदि एक समबाहु त्रिभुज का क्षेत्रफल 36 sqrt3 वर्ग सेमी है, तो इस त्रिभुज का परिमाप कितना होगा ?
View Solution
